Home
Reasoning
Aptitude
Previous Papers
General Knowledge
Top 10

Time and Work Shortcuts, Formulas, Video

Recommend Book

100% Sucess Rate

29,000+ TCS MCQs

Stay ahead in your all SSC exam journey with ‘SSC Game Changer English, Maths, General Awareness, Reasoning Combo Set of 4 Books’. Designed for strategic preparation, this book offers 29,000+ TCS MCQs, 25 online CBTs, and detailed exam analysis to help aspirants improve accuracy, boost confidence, and maximize scores. Stay updated with the monthly current affairs magazine and gain a competitive edge to achieve success!

Shortcut and Formula on Time and Work

Work from Days:
If A can do a piece of work in n days, then A's 1 day's work =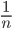 $\frac{1}{n}$

Days from Work:
If A's 1 day's work =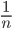 $\frac{1}{n}$ , then A can finish the work in n days.

Ratio:
If A is thrice as good a workman as B, then:
Ratio of work done by A and B = 3 : 1.
Ratio of times taken by A and B to finish a work = 1 : 3.

If A is 'x' times as good a workman as B, then he will take of the time by B to do the same work.

A and B can do a piece of work in 'a' days and 'b' days respectively, then working together, they will take $\frac{xy}{x+y}$ days to finish the work and in one day, they will finish $\frac{xy}{x+y}th$ part of work.

Time and Work Previous Year Questions

Time limit: 0

Quiz-summary

0 of 50 questions completed

Questions:

Information

Work, Time, Speed and Distance

You have already completed the quiz before. Hence you can not start it again.

Quiz is loading...

You must sign in or sign up to start the quiz.

You have to finish following quiz, to start this quiz:

Results

0 of 50 questions answered correctly

Your time:

Time has elapsed

You have reached 0 of 0 points, (0)

Average score
Your score

Categories

Not categorized 0%

Answered
Review

Question 1 of 50

1. Question
Mohan can finish a job in 60 days whereas Ram can finish the same job in 20 days. If they work together the job will be over in
- $7 \frac{1}{2}$
- 15 days
- 20 days
- 80 days
Correct

$\frac{1}{t}= \frac{1}{60}+ \frac{1}{20}= \frac{1}{15}$

$\Rightarrow$ time = 15 days

Incorrect

$\frac{1}{t}= \frac{1}{60}+ \frac{1}{20}= \frac{1}{15}$

$\Rightarrow$ time = 15 days
Question 2 of 50

2. Question
A can do a piece of work in 20 days and B can do it in 30 days. Time taken by them to finish the job working together is
- 9 days
- 12 days
- $12 \frac{1}{2}$
- 6 days
Correct

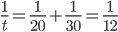
$\frac{1}{t}= \frac{1}{20}+ \frac{1}{30}= \frac{1}{12}$

$\Rightarrow$ time = 12 days

Incorrect

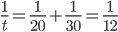
$\frac{1}{t}= \frac{1}{20}+ \frac{1}{30}= \frac{1}{12}$

$\Rightarrow$ time = 12 days
Question 3 of 50

3. Question
A can type 75 pages in 25 hours. A and B working together can type 135 pages in 27 hours. Time needed by B to type 42 pages is
- 24 hours
- 18 hours
- 21 hours
- 16 hours
Correct

A can type 3 pages in 1 hour

A and B can together type 5 pages in 1 hour

$\Rightarrow$ B can type 2 pages in an hour

$\Rightarrow$ B needs 21 hours to type 42 pages

Incorrect

A can type 3 pages in 1 hour

A and B can together type 5 pages in 1 hour

$\Rightarrow$ B can type 2 pages in an hour

$\Rightarrow$ B needs 21 hours to type 42 pages
Question 4 of 50

4. Question
A and B working together can do a piece of work in 7 days. B along can do it in 8 days. After working alone on it for 5 days, B leaves the job. The work is taken over by A. The time needed by A to finish the job is
- 21 days
- 16 days
- 18 days
- None of above
Correct

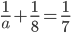
$\frac{1}{a}+ \frac{1}{8}= \frac{1}{7}$

$\Rightarrow \frac{1}{a}=\frac{1}{7} - \frac{1}{8}= \frac{1}{56}$

$5 \times \frac{1}{8}+n \times \frac{1}{56}=1$

$\Rightarrow$ n = 21

Incorrect

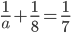
$\frac{1}{a}+ \frac{1}{8}= \frac{1}{7}$

$\Rightarrow \frac{1}{a}=\frac{1}{7} - \frac{1}{8}= \frac{1}{56}$

$5 \times \frac{1}{8}+n \times \frac{1}{56}=1$

$\Rightarrow$ n = 21
Question 5 of 50

5. Question
X can finish a job in 12 days, Y in 18 days and Z in 9 days. If they work together the job will be over in
- 5 days
- 4 days
- 10 days
- 9 days
Correct

$\frac{1}{t}=\frac{1}{12}+ \frac{1}{18}+\frac{1}{9}= \frac{1}{4}$

$\Rightarrow$ time = 4 days

Incorrect

$\frac{1}{t}=\frac{1}{12}+ \frac{1}{18}+\frac{1}{9}= \frac{1}{4}$

$\Rightarrow$ time = 4 days
Question 6 of 50

6. Question
A can dig a well in 10 days, B can dig it in 12 days and C can dig it is 15 days. If all work together the well be dug in
- 6 days
- 4 days
- 3 days
- 2 days
Correct

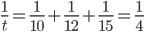
$\frac{1}{t}=\frac{1}{10}+ \frac{1}{12}+\frac{1}{15}= \frac{1}{4}$

$\Rightarrow$ time = 4 days

Incorrect

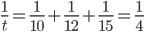
$\frac{1}{t}=\frac{1}{10}+ \frac{1}{12}+\frac{1}{15}= \frac{1}{4}$

$\Rightarrow$ time = 4 days
Question 7 of 50

7. Question
A can do a piece of work in 5 days, B in 4 days and A, B and C in 2 days. Time needed by C to complete the job is
- 20 days
- 40 days
- 10 days
- None of above
Correct

$\frac{1}{5}+ \frac{1}{4}+ \frac{1}{c}= \frac{1}{2}$

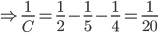
$\Rightarrow \frac{1}{C}=\frac{1}{2}- \frac{1}{5}-\frac{1}{4}= \frac{1}{20}$

$\Rightarrow$ time = 20 days

Incorrect

$\frac{1}{5}+ \frac{1}{4}+ \frac{1}{c}= \frac{1}{2}$

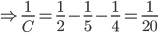
$\Rightarrow \frac{1}{C}=\frac{1}{2}- \frac{1}{5}-\frac{1}{4}= \frac{1}{20}$

$\Rightarrow$ time = 20 days
Question 8 of 50

8. Question
A and B working together can mow a field in 28 days. With help of C they can finish the job in 21 days. If C works all alone the time needed by him to finish the job is
- 42 days
- 84 days
- 63 days
- None of above
Correct

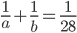
$\frac{1}{a}+ \frac{1}{b}= \frac{1}{28}$

$\frac{1}{a}+ \frac{1}{b}+ \frac{1}{c} = \frac{1}{21}$

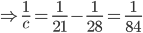
$\Rightarrow \frac{1}{c} = \frac{1}{21}- \frac{1}{28}= \frac{1}{84}$

$\Rightarrow$ time = 84 days

Incorrect

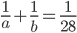
$\frac{1}{a}+ \frac{1}{b}= \frac{1}{28}$

$\frac{1}{a}+ \frac{1}{b}+ \frac{1}{c} = \frac{1}{21}$

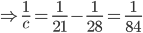
$\Rightarrow \frac{1}{c} = \frac{1}{21}- \frac{1}{28}= \frac{1}{84}$

$\Rightarrow$ time = 84 days
Question 9 of 50

9. Question
A and B working together can finish a job in 2 days. If B alone can do it in 3 days then A alone can do it in
- 6 days
- 4 days
- 8 days
- 5 days
Correct

$\frac{1}{a}+ \frac{1}{3}= \frac{1}{2}$

$\Rightarrow \frac{1}{a}= \frac{1}{2} -\frac{1}{3}= \frac{1}{6}$

$\Rightarrow$ time = 6 days

Incorrect

$\frac{1}{a}+ \frac{1}{3}= \frac{1}{2}$

$\Rightarrow \frac{1}{a}= \frac{1}{2} -\frac{1}{3}= \frac{1}{6}$

$\Rightarrow$ time = 6 days
Question 10 of 50

10. Question
A and B together can do a job in 24 days; B and C together in 18 days; and C and A together in 36 days. If they all work together the job will be over in
- 8 days
- 16 days
- 10 days
- 32 days
Correct

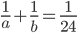
$\frac{1}{a}+ \frac{1}{b}= \frac{1}{24}$

$\frac{1}{b}+\frac{1}{c}= \frac{1}{18}$

$\frac{1}{c}+\frac{1}{a}=\frac{1}{36}$

Adding $2( \frac{1}{a}+ \frac{1}{b}+ \frac{1}{c})= \frac{1}{24}+ \frac{1}{18}+ \frac{1}{36}= \frac{1}{8}$

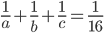
$\frac{1}{a}+ \frac{1}{b}+ \frac{1}{c}=\frac{1}{16}$

$\Rightarrow$ time = 16 days

Incorrect

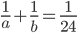
$\frac{1}{a}+ \frac{1}{b}= \frac{1}{24}$

$\frac{1}{b}+\frac{1}{c}= \frac{1}{18}$

$\frac{1}{c}+\frac{1}{a}=\frac{1}{36}$

Adding $2( \frac{1}{a}+ \frac{1}{b}+ \frac{1}{c})= \frac{1}{24}+ \frac{1}{18}+ \frac{1}{36}= \frac{1}{8}$

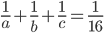
$\frac{1}{a}+ \frac{1}{b}+ \frac{1}{c}=\frac{1}{16}$

$\Rightarrow$ time = 16 days
Question 11 of 50

11. Question
A and B can finish a job in 12 days; B and C in 15 days and C and A in 20 days. Working alone C can finish the job in
- 60 days
- 90 days
- 108 days
- 12 days
Correct

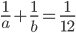
$\frac{1}{a}+ \frac{1}{b}=\frac{1}{12}$

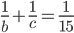
$\frac{1}{b}+ \frac{1}{c}=\frac{1}{15}$

$\frac{1}{c}+ \frac{1}{a}=\frac{1}{20}$

$2(\frac{1}{a}+ \frac{1}{b}+ \frac{1}{c}) =\frac{1}{5}$

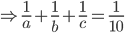
$\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c} =\frac{1}{10}$

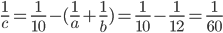
$\frac{1}{c} =\frac{1}{10}-(\frac{1}{a}+\frac{1}{b})= \frac{1}{10}- \frac{1}{12}= \frac{1}{60}$

$\Rightarrow$ time = 60 days

Incorrect

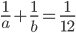
$\frac{1}{a}+ \frac{1}{b}=\frac{1}{12}$

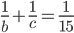
$\frac{1}{b}+ \frac{1}{c}=\frac{1}{15}$

$\frac{1}{c}+ \frac{1}{a}=\frac{1}{20}$

$2(\frac{1}{a}+ \frac{1}{b}+ \frac{1}{c}) =\frac{1}{5}$

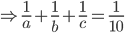
$\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c} =\frac{1}{10}$

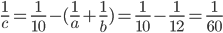
$\frac{1}{c} =\frac{1}{10}-(\frac{1}{a}+\frac{1}{b})= \frac{1}{10}- \frac{1}{12}= \frac{1}{60}$

$\Rightarrow$ time = 60 days
Question 12 of 50

12. Question
A can do a job in 24 days. B is 50% more efficient than A. Then B can finish the job in
- 16 days
- 12 days
- 18 days
- 10 days
Correct

B needs half the time

$\Rightarrow B\;needs\:24 \times \frac{1}{2} =12 days$

Incorrect

B needs half the time

$\Rightarrow B\;needs\:24 \times \frac{1}{2} =12 days$
Question 13 of 50

13. Question
A can do twice as much work as B. If they can together finish the job in 24 days, then working alone A would have finished the job in
- 72days
- 42 days
- 36 days
- 121 days
Correct

$\frac{1}{x}+ \frac{1}{2x}= \frac{1}{24}$

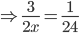
$\Rightarrow \frac{3}{2x}= \frac{1}{24}$

$\Rightarrow$ x = 36

Hence A requires 36 days

Incorrect

$\frac{1}{x}+ \frac{1}{2x}= \frac{1}{24}$

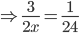
$\Rightarrow \frac{3}{2x}= \frac{1}{24}$

$\Rightarrow$ x = 36

Hence A requires 36 days
Question 14 of 50

14. Question
3 men or 5 women can reap a field in 43 days. Time needed by 5 men and 6 women to do the same is
- $7 \frac{1}{2}$
- 15 days
- 16 days
- 30 days
Correct

Work done by 1 man in 1 day= $\frac{1}{3 \times 43}= \frac{1}{129}$

Work done by 1 woman in 1 day = $\frac{1}{5 \times 43}= \frac{1}{215}$

Work done by 5 men and 6 women in 1 day = $\frac{5}{129}+ \frac{6}{215}= \frac{1}{15}$

Hence work will be over in 15 days.

Incorrect

Work done by 1 man in 1 day= $\frac{1}{3 \times 43}= \frac{1}{129}$

Work done by 1 woman in 1 day = $\frac{1}{5 \times 43}= \frac{1}{215}$

Work done by 5 men and 6 women in 1 day = $\frac{5}{129}+ \frac{6}{215}= \frac{1}{15}$

Hence work will be over in 15 days.
Question 15 of 50

15. Question
If 3 men or 4 women can do a piece of work in 43 days, then time needed by 7 men and 5 women to do the same work is
- 18 days
- 16 days
- 12 days
- 20 days
Correct

Work done by 1 man in 1 day = $\frac{1}{3 \times 43}= \frac{1}{129}$

Work done by 1 woman in 1 day= $\frac{1}{4 \times 43}= \frac{1}{172}$

Work done by 7 women and 5 women in 1 day

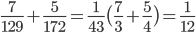
= $\frac{7}{129}+ \frac{5}{172}= \frac{1}{43} \big( \frac{7}{3}+ \frac{5}{4} \big)= \frac{1}{12}$

Hence work will be over in 12 days.

Incorrect

Work done by 1 man in 1 day = $\frac{1}{3 \times 43}= \frac{1}{129}$

Work done by 1 woman in 1 day= $\frac{1}{4 \times 43}= \frac{1}{172}$

Work done by 7 women and 5 women in 1 day

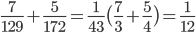
= $\frac{7}{129}+ \frac{5}{172}= \frac{1}{43} \big( \frac{7}{3}+ \frac{5}{4} \big)= \frac{1}{12}$

Hence work will be over in 12 days.
Question 16 of 50

16. Question
30 men and 14 boys can reap a field in 121 days. If 3 men do as much work as 5 boys then 20 men and 4 boys will receipt in
- 18 days
- 27 days
- 26 days
- None of the above
Correct

$\frac{30}{m}+ \frac{40}{b} =\frac{1}{21}$ …… (i)

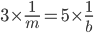
$3 \times \frac{1}{m} = 5 \times \frac{1}{b}$

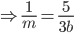
$\Rightarrow \frac{1}{m}= \frac{5}{3b}$

Substituting in (i)

We get $\frac{1}{b}= \frac{1}{1050}\:and\: \frac{1}{m}= \frac{1}{630}$

Work done by 20 men and 4 boys in 1 day

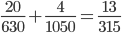
= $\frac{20}{630}+\frac{4}{1050}= \frac{13}{315}$

Hence work will be over in $\frac{315}{13}=24 \frac{3}{13}\:days$

Incorrect

$\frac{30}{m}+ \frac{40}{b} =\frac{1}{21}$ …… (i)

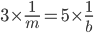
$3 \times \frac{1}{m} = 5 \times \frac{1}{b}$

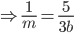
$\Rightarrow \frac{1}{m}= \frac{5}{3b}$

Substituting in (i)

We get $\frac{1}{b}= \frac{1}{1050}\:and\: \frac{1}{m}= \frac{1}{630}$

Work done by 20 men and 4 boys in 1 day

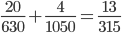
= $\frac{20}{630}+\frac{4}{1050}= \frac{13}{315}$

Hence work will be over in $\frac{315}{13}=24 \frac{3}{13}\:days$
Question 17 of 50

17. Question
A takes half as long to do a piece of work as B takes and if C does it in same time as A and B together, and if all three working together will take 7 days to complete the work then B working alone would finish the job in
- 21 days
- 14 days
- 42 days
- $21 \frac{2}{3}\:days$
Correct

$\frac{1}{c}= \frac{2}{x}+ \frac{1}{x}= \frac{3}{x}$

$\frac{1}{a}+ \frac{1}{b}+\frac{1}{c}= \frac{2}{x}+ \frac{1}{x}+\frac{3}{x}= \frac{6}{x}= \frac{1}{7}$

$\Rightarrow$ x = 42

$\Rightarrow$ time = 42 days

Incorrect

$\frac{1}{c}= \frac{2}{x}+ \frac{1}{x}= \frac{3}{x}$

$\frac{1}{a}+ \frac{1}{b}+\frac{1}{c}= \frac{2}{x}+ \frac{1}{x}+\frac{3}{x}= \frac{6}{x}= \frac{1}{7}$

$\Rightarrow$ x = 42

$\Rightarrow$ time = 42 days
Question 18 of 50

18. Question
A can do as much work in 3 days as C in 4 days and B can do as much work in 5 days as C in 6 days. Time needed by B to finish a work which A can finish in 18 days is
- 20 days
- 10 days
- 15 days
- 24 days
Correct

$\frac{3}{a}= \frac{4}{c}\:and\: \frac{5}{b}= \frac{6}{c}$

$\Rightarrow \frac{3}{4a}= \frac{1}{c}\:and\: \frac{5}{6b}= \frac{1}{c}$

$\Rightarrow \frac{3}{4a}= \frac{5}{6b}$

But $\frac{1}{a}= \frac{1}{18}$

$\Rightarrow \frac{1}{b}= \frac{3}{4} \times \frac{1}{18}\times \frac{6}{5}= \frac{1}{20}$

$\Rightarrow$ b needs 20 days to finish the work

Incorrect

$\frac{3}{a}= \frac{4}{c}\:and\: \frac{5}{b}= \frac{6}{c}$

$\Rightarrow \frac{3}{4a}= \frac{1}{c}\:and\: \frac{5}{6b}= \frac{1}{c}$

$\Rightarrow \frac{3}{4a}= \frac{5}{6b}$

But $\frac{1}{a}= \frac{1}{18}$

$\Rightarrow \frac{1}{b}= \frac{3}{4} \times \frac{1}{18}\times \frac{6}{5}= \frac{1}{20}$

$\Rightarrow$ b needs 20 days to finish the work
Question 19 of 50

19. Question
A can finish a job in 15 days and B can do it in 10 days. If they work together then A’s share out of total wages of Rs. 2250 is
- Rs. 1350
- Rs. 900
- Rs. 1025
- Rs. 1125
Correct

A : B = $\frac{1}{15}: \frac{1}{10}=10:15$

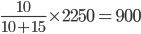A’ share = $\frac{10}{10+15} \times 2250=900$

Incorrect

A : B = $\frac{1}{15}: \frac{1}{10}=10:15$

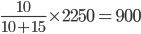
A’ share = $\frac{10}{10+15} \times 2250=900$
Question 20 of 50

20. Question
A can do a piece of work in 8 days and B can do the same work in 12 days. A and B together Complete the job and get Rs. 200 as combined wages. B’s share in the wage will be
- Rs. 80
- Rs. 82
- Rs. 85
- Rs. 75
Correct

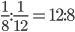
A:B = $\frac{1}{8}: \frac{1}{12}=12:8$

B’s share = $\frac{8}{8+12} \times 200 = 80$

Incorrect

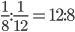
A:B = $\frac{1}{8}: \frac{1}{12}=12:8$

B’s share = $\frac{8}{8+12} \times 200 = 80$
Question 21 of 50

21. Question
Two men A and B working together completed a piece of work which would have taken them respectively 12 and 18 days to complete if they had worked separately. They received a payment of Rs. 29,850. Then share of A is
- Rs. 11940
- Rs. 17910
- Rs. 11900
- Rs. 18000
Correct

A : B = $\frac{1}{12}: \frac{1}{18} =18 : 12$

A’ share = $\frac{18}{12+18} \times 29850 = 17910$

Incorrect

A : B = $\frac{1}{12}: \frac{1}{18} =18 : 12$

A’ share = $\frac{18}{12+18} \times 29850 = 17910$
Question 22 of 50

22. Question
A, B and C together do a piece of work for Rs. 5350. A working alone could do it in 5 days, B in 6 days and C in 7 days. The share of C is
- Rs. 1500
- Rs. 2100
- Rs. 1750
- None of above
Correct

A : B : C = $\frac{1}{5}: \frac{1}{6}: \frac{1}{7}=42:35:30$

C’s share = $\frac{30}{42+35+30} \times 5350 = 1500$

Incorrect

A : B : C = $\frac{1}{5}: \frac{1}{6}: \frac{1}{7}=42:35:30$

C’s share = $\frac{30}{42+35+30} \times 5350 = 1500$
Question 23 of 50

23. Question
Wages of 45 women amount to Rs. 93150 in 48 days, Daily wage of a man is twice that of a women. The number of men who in 16 days will earn Rs. 34500
- 20
- 30
- 35
- 25
Correct

Wages of $45 \times 48$ women days = 93150

Wages of 1 woman day = $\frac{93150}{45 \times 48} = Rs. 43.125$

Wage of 1 man day = $2 \times 43.125 = Rs. 86.25$

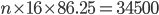
$n \times 16 \times 86.25 =34500$

n = 25

Incorrect

Wages of $45 \times 48$ women days = 93150

Wages of 1 woman day = $\frac{93150}{45 \times 48} = Rs. 43.125$

Wage of 1 man day = $2 \times 43.125 = Rs. 86.25$

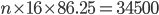
$n \times 16 \times 86.25 =34500$

n = 25
Question 24 of 50

24. Question
A Field can be reaped by 10 women in 4 days or by 6 boys in 10 days or by 2 men in 12 days. 1 man, 3 boys and 2 women are employed. If the daily wages of a man, a woman and a child are Rs. 153, Rs. 93 and Rs. 57 respectively then the total expense of reaping the field is
- Rs. 1800
- Rs. 3600
- Rs. 2700
- None of above
Correct

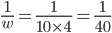
$\frac{1}{w}= \frac{1}{10 \times 4}= \frac{1}{40}$

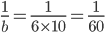
$\frac{1}{b}= \frac{1}{6 \times 10}= \frac{1}{60}$

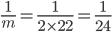
$\frac{1}{m}= \frac{1}{2 \times 22}= \frac{1}{24}$

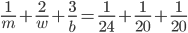
$\frac{1}{m}+ \frac{2}{w}+ \frac{3}{b} = \frac{1}{24}+ \frac{1}{20}+ \frac{1}{20}$

= $\frac{5+6+6}{120}= \frac{17}{120}$

Work will be over in $\frac{120}{17}\:days$

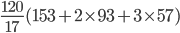
Wages = $\frac{120}{17}(153+2 \times 93+3 \times 57)$

= Rs.3600

Incorrect

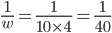
$\frac{1}{w}= \frac{1}{10 \times 4}= \frac{1}{40}$

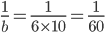
$\frac{1}{b}= \frac{1}{6 \times 10}= \frac{1}{60}$

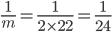
$\frac{1}{m}= \frac{1}{2 \times 22}= \frac{1}{24}$

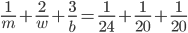
$\frac{1}{m}+ \frac{2}{w}+ \frac{3}{b} = \frac{1}{24}+ \frac{1}{20}+ \frac{1}{20}$

= $\frac{5+6+6}{120}= \frac{17}{120}$

Work will be over in $\frac{120}{17}\:days$

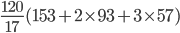
Wages = $\frac{120}{17}(153+2 \times 93+3 \times 57)$

= Rs.3600
Question 25 of 50

25. Question
4 men earn as much in a day as 7 women; and 1 woman earns as much in a day as 2 boys. If 6 men, 10 women and 14 boys working together for 8 days earn Rs. 9900 then 8 men and 6 women working together for 10 days will earn
- Rs. 9500
- Rs. 9000
- Rs. 9900
- None of above
Correct

Incorrect
Question 26 of 50

26. Question
The distance between two stations A and B is 300 km. A train leaves the station A with a speed of 40 km/hr. At the same time another train depart from the station B with a speed of 50 km/h. The time after which these two trains to meet each other is
- 3 hrs 40 min
- 3 hrs 20 min
- 2 hrs 20 min
- 2 hrs 24 min
Correct

Relative speed = 40 + 50 90 km/hr

Distance = 300 km

Time = 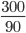$\frac{300}{90}$ = 3 hrs 20 minutes.

Incorrect

Relative speed = 40 + 50 90 km/hr

Distance = 300 km

Time = 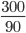$\frac{300}{90}$ = 3 hrs 20 minutes.
Question 27 of 50

27. Question
A passenger train takes two hours less for a journey of 300 km if its speed is increased by 5 km/hr from its normal speed. The normal speed is
- 35 km/hr
- 50 km/hr
- 25 km/hr
- 30 km/hr
Correct

Let the normal speed by x km/hr

Then, $\frac{300}{x}- \frac{300}{x+5}=2$ Solving x = 25

Incorrect

Let the normal speed by x km/hr

Then, $\frac{300}{x}- \frac{300}{x+5}=2$ Solving x = 25
Question 28 of 50

28. Question
The speed of a metro train is 54 km/hr excluding stoppage time and if including stoppage, the speed is 45 km/hr, then for how many minutes does it stop per hour?
- 9
- 10
- 20
- 11
Correct

Stoppage time is the time taken to cover a distance of (54-45) km at the speed of 54 km/h

54 Km : 60 min = 9 km : x min

Solving x = 10

Incorrect

Stoppage time is the time taken to cover a distance of (54-45) km at the speed of 54 km/h

54 Km : 60 min = 9 km : x min

Solving x = 10
Question 29 of 50

29. Question
An express train runs an average speed 100 kmph stopping 3 minutes after 75 km. A local train runs at a speed of 50 kmph, stopping for 1 minute after every 25 km. If the train began running at the same time, how many kilometers did the local train run in the time it took the express train to run 600 km?
- 307.5 km
- 900 km
- 1200 km
- 1000 km
Correct

For express train : time to run 600 km = 6hrs. But this also includes 7 stoppages of 3 minutes each. Hence total time = 6 hrs 21 minutes or (381 minutes)

The local train covers 25 km in every 31 minutes.

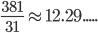
$\frac{381}{31} \approx 12.29.....$

This mean train has covered $25 \times 12 km\:(300 km)\:in\:12 \times 31\:minutes\:(372 minutes)$

still 9 minutes are left.

The train covers another $\frac{9}{60} \times 50 km =7.5 km$

Hence total distance travelled = 307.5 km.

Incorrect

For express train : time to run 600 km = 6hrs. But this also includes 7 stoppages of 3 minutes each. Hence total time = 6 hrs 21 minutes or (381 minutes)

The local train covers 25 km in every 31 minutes.

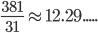
$\frac{381}{31} \approx 12.29.....$

This mean train has covered $25 \times 12 km\:(300 km)\:in\:12 \times 31\:minutes\:(372 minutes)$

still 9 minutes are left.

The train covers another $\frac{9}{60} \times 50 km =7.5 km$

Hence total distance travelled = 307.5 km.
Question 30 of 50

30. Question
Excluding stoppages, the speed of a bus is 54 km/h and including stoppages, it is 36 km/h. The stoppage time of the bus in minutes is
- 9
- 20
- 12
- 8
Correct

Had the bus not stopped it would have covered 18 km more in one hour. So stoppage time is the time needed to cover 18 km at the speed of 54 km/hr

54 km : 60 min = 18 km : x min

X= 20

Incorrect

Had the bus not stopped it would have covered 18 km more in one hour. So stoppage time is the time needed to cover 18 km at the speed of 54 km/hr

54 km : 60 min = 18 km : x min

X= 20
Question 31 of 50

31. Question
An insect climbs up a 10 metre high pole. It climbs up 3 metres in the first minute but step down 2 metres in the second minute again climbs up 3 metres in the third minute and step down 2 metres in the fourth minute and so on. It reaches the top of the pole in
- 15 minutes
- 17 minutes
- 19 minutes
- 20 minutes
Correct

The insect ascends (3-2) m or 1 min ever two minutes.
To ascend 7 m the insect needs 14 minutes.
Now in the fifteenth minute he ascends 3 m and reaches the top of the pole.

Incorrect

The insect ascends (3-2) m or 1 min ever two minutes.
To ascend 7 m the insect needs 14 minutes.
Now in the fifteenth minute he ascends 3 m and reaches the top of the pole.
Question 32 of 50

32. Question
If a man travels at 30 km/hr, then the reaches his destination late by 10 minutes and if he travels at 42 km/hr, then he reaches 10 minutes earlier. Therefore the distance travelled by him is
- 36 km
- 35 km
- 40 km
- 48 km
Correct

Let the distance be x km and the required time be t hrs

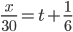
Then, $\frac{x}{30}=t+ \frac{1}{6}$

And $\frac{x}{42}=t- \frac{1}{6}$

$\frac{x}{30} - \frac{x}{42}= \big\{t+ \frac{1}{6} \big\}- \big\{t- \frac{1}{6} \big\}$

Incorrect

Let the distance be x km and the required time be t hrs

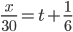
Then, $\frac{x}{30}=t+ \frac{1}{6}$

And $\frac{x}{42}=t- \frac{1}{6}$

$\frac{x}{30} - \frac{x}{42}= \big\{t+ \frac{1}{6} \big\}- \big\{t- \frac{1}{6} \big\}$
Question 33 of 50

33. Question
Which of the following trains is the fastest?
- 36 km
- 35 km
- 40 km
- 48 km
Correct

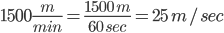
$1500 \frac{m}{min}= \frac{1500\:m}{60\:sec}=25\:m/sec$

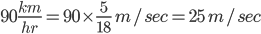
$90\frac{km}{hr}= 90 \times \frac{5}{18}\:m/sec=25\:m/sec$

All options (a), (b) and (c) have equal value. Hence option (d) is correct.

Incorrect

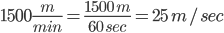
$1500 \frac{m}{min}= \frac{1500\:m}{60\:sec}=25\:m/sec$

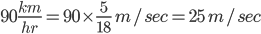
$90\frac{km}{hr}= 90 \times \frac{5}{18}\:m/sec=25\:m/sec$

All options (a), (b) and (c) have equal value. Hence option (d) is correct.
Question 34 of 50

34. Question
A Speed of $33 \frac{1}{3}$ metres/second is the same as
- 100 km/hr
- 80 km/hr
- 120 km/hr
- 75 km/hr
Correct

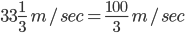
$33 \frac{1}{3}\;m/sec = \frac{100}{3}\:m/sec$

= $\frac{100}{3} \times \frac{18}{5}\:km/hr$

= 120 km/hr.

Incorrect

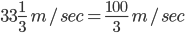
$33 \frac{1}{3}\;m/sec = \frac{100}{3}\:m/sec$

= $\frac{100}{3} \times \frac{18}{5}\:km/hr$

= 120 km/hr.
Question 35 of 50

35. Question
A and B are 25 km apart. If they travel in opposite directions, they meet an hour. If they travel in the same direction, they meet after 5 hours. If A travel faster than B, then the speed of A is
- 10 km/hr
- 12.5 km/hr
- 15 km/hr
- 20 km/hr
Correct

Let speeds of A and B be x km/hr and y km/hr respectively.

Then, x +y = $\frac{25}{1}=25$

And x – y = $\frac{25}{5}=5$

Solving: x = 15

$\therefore$ Speed of A is 15 km/hr

Incorrect

Let speeds of A and B be x km/hr and y km/hr respectively.

Then, x +y = $\frac{25}{1}=25$

And x – y = $\frac{25}{5}=5$

Solving: x = 15

$\therefore$ Speed of A is 15 km/hr
Question 36 of 50

36. Question
A specific distance (x km) is to be covered in a specific time. If a car runs at a speed of 20 km per hour, then it reaches late by 15 minutes. If its speed is 40 km per hour, then it reaches 15 minutes earlier. The value of x would be
- 10
- 20
- 150
- 200
Correct

$\frac{x}{20}=t+ \frac{1}{4}$

$\frac{x}{40}=t- \frac{1}{4}$

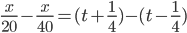
$\frac{x}{20} - \frac{x}{40}= (t+ \frac{1}{4}) - (t- \frac{1}{4})$

$\frac{x}{40}= \frac{1}{2}$

X = 20

Incorrect

$\frac{x}{20}=t+ \frac{1}{4}$

$\frac{x}{40}=t- \frac{1}{4}$

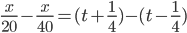
$\frac{x}{20} - \frac{x}{40}= (t+ \frac{1}{4}) - (t- \frac{1}{4})$

$\frac{x}{40}= \frac{1}{2}$

X = 20
Question 37 of 50

37. Question
A twice as fast as B and B is thrice as fast as C is. The journey covered by C in 42 minutes will be covered by A in
- 14 min
- 7 min
- 28 min
- 21 min
Correct

Time for C = 42 min

Time for B = $\frac{42}{3}$ = 14 min

Time for A = $\frac{142}{2}$ = 7 min

Incorrect

Time for C = 42 min

Time for B = $\frac{42}{3}$ = 14 min

Time for A = $\frac{142}{2}$ = 7 min
Question 38 of 50

38. Question
38 When two trains were running in the same direction at 90 km/hr and 70 km/hr respectively, then the faster train passed a man sitting in the slower train in 36 seconds. Find the length of faster train.
- 100 metres
- 150 metres
- 190 metres
- 200 metres
Correct

Relative speed = (90 – 70) km/hr = 20 km/hr

= $20 \times \frac{5}{18}\:m/sec$

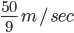
= $\frac{50}{9}\:m/sec$

Time = 36 seconds

$\Rightarrow length\:of\:faster\:train= \frac{50}{9} \times 36\:m$

= 200 m

Incorrect

Relative speed = (90 – 70) km/hr = 20 km/hr

= $20 \times \frac{5}{18}\:m/sec$

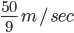
= $\frac{50}{9}\:m/sec$

Time = 36 seconds

$\Rightarrow length\:of\:faster\:train= \frac{50}{9} \times 36\:m$

= 200 m
Question 39 of 50

39. Question
Two trains, each 120 metres in lengths, run in opposite directions with velocities of 40 m/sec. and 20 m/sec. respectively. How long will it take for the tail end of two trains to meet each other from the time their engines crossed each other?
- 22 seconds
- 23 seconds
- 14.4 seconds
- 15 seconds
Correct

Distance = (120 + 120) m

= 240 m

Relative speed = (40 + 20) km/hr = 60 km/hr

= $\frac{50}{3}\:m/sec$

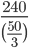Time = $\frac{240}{ \big( \frac{50}{3} \big) }$ sec = 14.4 sec

Incorrect

Distance = (120 + 120) m

= 240 m

Relative speed = (40 + 20) km/hr = 60 km/hr

= $\frac{50}{3}\:m/sec$

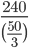Time = $\frac{240}{ \big( \frac{50}{3} \big) }$ sec = 14.4 sec
Question 40 of 50

40. Question
A train speeds past a pole in 15 seconds and speeds past a platform of 100 metres long in 30 seconds. Its length (in metres) is
- 200
- 100
- 50
- Data inadequate
Correct

Let the length of the train be x m and its speed be s m/sec.

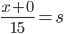Then $\frac{x+0}{15}=s$ (we assume the horizontal length of the pole to be o m)

And $\frac{x+100}{30}=s$

$\Rightarrow \frac{x}{15}= \frac{x+100}{30}$

Solving x =100

$\Rightarrow$ Length of train is 100 m

Incorrect

Let the length of the train be x m and its speed be s m/sec.

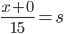Then $\frac{x+0}{15}=s$ (we assume the horizontal length of the pole to be o m)

And $\frac{x+100}{30}=s$

$\Rightarrow \frac{x}{15}= \frac{x+100}{30}$

Solving x =100

$\Rightarrow$ Length of train is 100 m
Question 41 of 50

41. Question
A train running at the speed of 54 km/hr completely crosses a platform in 20 seconds. If the platforms is 100 m long the length of the train in metres is
- 100
- 200
- 300
- 400
Correct

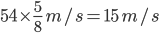
54 km/hr = $54 \times \frac{5}{8}\:m/s=15\:m/s$

Time = 20 sec

Let length of the train be x, then 100 + x = $15 \times 20=300$

So length of the train is = 200 m

Incorrect

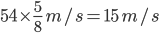
54 km/hr = $54 \times \frac{5}{8}\:m/s=15\:m/s$

Time = 20 sec

Let length of the train be x, then 100 + x = $15 \times 20=300$

So length of the train is = 200 m
Question 42 of 50

42. Question
A train 120 m long completely crosses a platform 55 m long in 10 seconds. Speed of the train in km/h is
- 50
- 90
- 63
- 75
Correct

Speed = 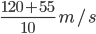$\frac{120+55}{10}\:m/s$ = 17.5 m/s = 63 km/hr

Incorrect

Speed = 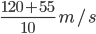$\frac{120+55}{10}\:m/s$ = 17.5 m/s = 63 km/hr
Question 43 of 50

43. Question
Two trains 101 m and 99 m long are running in opposite directions along parallel tracks at the speeds of 40 km/hr and 32 km/hr. The time taken by them is completely clear of each other in seconds is
- 9
- 12
- 20
- 10
Correct

Relative speed 40 + 32 = 72 km/hr = $72 \times \frac{5}{18}\:m/s=20\:m/s$

Sum of lengths = 200 m so time = $\frac{200}{20}\:sec=10\:sec$

Incorrect

Relative speed 40 + 32 = 72 km/hr = $72 \times \frac{5}{18}\:m/s=20\:m/s$

Sum of lengths = 200 m so time = $\frac{200}{20}\:sec=10\:sec$
Question 44 of 50

44. Question
Two trains are running in opposite directions along parallel tracks at the speeds of 50 km/hr and 40 km/hr take 8 seconds to completely clear off each other. If the faster train is 125 m long, the length of the shorter train in metres is
- 75
- 100
- 125
- 120
Correct

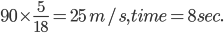
Relative speed = 50 + 40 = 90 km/hr = $90 \times \frac{5}{18}=25\:m/s,time = 8 sec.$

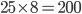
Let length of the first train be x m, then (125 + x) = $25 \times 8=200$

Hence length of the first train = 75 m

Incorrect

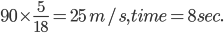
Relative speed = 50 + 40 = 90 km/hr = $90 \times \frac{5}{18}=25\:m/s,time = 8 sec.$

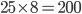
Let length of the first train be x m, then (125 + x) = $25 \times 8=200$

Hence length of the first train = 75 m
Question 45 of 50

45. Question
Two trains 120 m and 160 m long running in opposite direction along parallel tracks took 8 seconds to completely clear off each other. If the speed of one of the trains is 70 km/hr then the speed of the other train in km/hr is
- 60
- 56
- 63
- 65
Correct

Sum of lengths = 280 m

Time = 8 seconds

Relative speed = 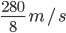$\frac{280}{8}\:m/s$ = 35 m/s = 126 km/hr

70 + x = 136

Or x = 56 km/hr

Incorrect

Sum of lengths = 280 m

Time = 8 seconds

Relative speed = 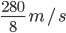$\frac{280}{8}\:m/s$ = 35 m/s = 126 km/hr

70 + x = 136

Or x = 56 km/hr
Question 46 of 50

46. Question
A steamer goes downstream and covers the distance between two towns in 20 hours. Coming back upstream it takes 5 hours more to do so. If speed of water is 4 km/hr, the distance between the two towns is
- 800 km
- 1600 km
- 1200 km
- 1000km
Correct

Distance downstream = distance upstream

$(x+40) \times 20= (x-4) \times 25$

$\Rightarrow$ x = 36

Distance = 800 km

Incorrect

Distance downstream = distance upstream

$(x+40) \times 20= (x-4) \times 25$

$\Rightarrow$ x = 36

Distance = 800 km
Question 47 of 50

47. Question
A race boat covers 33 km downstream in 55 minutes. To come back to the starting point it takes one hour. Speed of boat in still water is
- 40 km/hr
- 69 km/hr
- 34.5 km/hr
- 40.4 km/hr
Correct

Speed of downstream = 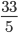$\frac{33}{5}$ km/min = 36 km/hr

Speed upstream = 33 km/hr

Speed of boat in still water = 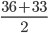$\frac{36+33}{2}$ km/hr = 34.5 km/hr

Incorrect

Speed of downstream = 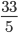$\frac{33}{5}$ km/min = 36 km/hr

Speed upstream = 33 km/hr

Speed of boat in still water = 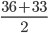$\frac{36+33}{2}$ km/hr = 34.5 km/hr
Question 48 of 50

48. Question
In one hour a boat goes 11 km along the stream or 5 km against the stream. The speed of the boat in still water (in km/hr) is
- 5
- 6
- 8
- 9
Correct

Let speed of boat in still water b x km/hr speed of stream by y km/hr.

Then x + y = 11

And x – y = 5

Solving x = 8

Hence speed of boat in still water = 8 km/hr

Incorrect

Let speed of boat in still water b x km/hr speed of stream by y km/hr.

Then x + y = 11

And x – y = 5

Solving x = 8

Hence speed of boat in still water = 8 km/hr
Question 49 of 50

49. Question
A boat goes 8 km in one hour along the stream and 2 km in one hour against the stream. The speed of the steam (in km/hr) is
- 2
- 3
- 4
- 5
Correct

Let speed of boat in still water be x km/hr and speed of stream by y km/hr

Then x + y = 8

And x – y =2

Solving y = 3

Hence speed of stream = 3 km/hr.

Incorrect

Let speed of boat in still water be x km/hr and speed of stream by y km/hr

Then x + y = 8

And x – y =2

Solving y = 3

Hence speed of stream = 3 km/hr.
Question 50 of 50

50. Question
A boat goes 6 km an hour in still water, but it takes thrice as much time in going the same distance against the current. The speed of the current (in km/hr) is
- 4
- 5
- 3
- 2
Correct

Let speed of boat in still water = 6 km/hr

Let speed of stream be x km/hr

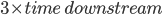
Time upstream = $3 \times time\:downstream$

$\Rightarrow Speed\:upstream= \frac{1}{3} \times speed \:downstream$

6 – x = $\frac{1}{3}\times (6+x) \Rightarrow 6-x=2+ \frac{x}{3}$

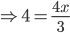
$\Rightarrow 4= \frac{4x}{3}$

$\Rightarrow$ x = 3

Hence speed of current is 3 km/hr.

Incorrect

Let speed of boat in still water = 6 km/hr

Let speed of stream be x km/hr

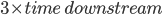
Time upstream = $3 \times time\:downstream$

$\Rightarrow Speed\:upstream= \frac{1}{3} \times speed \:downstream$

6 – x = $\frac{1}{3}\times (6+x) \Rightarrow 6-x=2+ \frac{x}{3}$

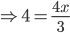
$\Rightarrow 4= \frac{4x}{3}$

$\Rightarrow$ x = 3

Hence speed of current is 3 km/hr.

Time and Work Video Lectures

Please comment on Time and Work Shortcuts, Formulas, Video

0 Comments

Submit a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Comment *

Name *

Email *

Website

Save my name, email, and website in this browser for the next time I comment.

Δ

Let’s Learn Together!

There’s no better way to see what we can offer to you than to actually use it. Tell us a bit about yourself so that we can set up your free personalized demo by simply filling out the form. Request a product tour to explore our online coaching system.

Designed by Softbranch | Managed by QuestionPaper