Important Formulas - Surds and Indices
- An integer is a whole number (positive, negative or zero). A rational number is one that can be expressed as a fraction
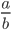 , where a and b are integers. All integers, fractions and terminating or recurring decimals are rational.
, where a and b are integers. All integers, fractions and terminating or recurring decimals are rational. - An irrational number cannot be expressed in the form
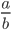 , where a and b are integers. Examples of irrational numbers are
, where a and b are integers. Examples of irrational numbers are  .
. - Real numbers are numbers that can be represented by points on the number line. Real numbers include both rational and irrational number.
- A surd is an irrational number involving a root. The numbers
![\sqrt{3},4\sqrt{5}\:and\:\sqrt[3]{7}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_b506921a60319f7695eed650b1cf9bda.gif) are examples of surds. Numbers such as
are examples of surds. Numbers such as ![\sqrt{16}and \sqrt[3]{8}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_9cfdf413b6dcb53345610bea2188ec2a.gif) are not surds because they are equal to rational numbers.
are not surds because they are equal to rational numbers.  =4 and root of ‘3’ or ‘root 3’. Note that we cannot take the square root of a negative number.
=4 and root of ‘3’ or ‘root 3’. Note that we cannot take the square root of a negative number. - Like surds involve the square root of the same number. Only like surds can be added or subtracted. For example,
 .
. - Surds of the form
 can be simplified if the number beneath the square root sign has a factor that is a perfect square. For example,
can be simplified if the number beneath the square root sign has a factor that is a perfect square. For example,  .
.
- The following rules can be used when multiplying or dividing surds.



- Rationalising the denominator of a surd means changing the denominator so that is a rational number. To rationalize the denominator of a surd such as
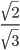 we use the result that
we use the result that so if we multiply the denominator by
so if we multiply the denominator by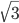 it will be rational. if we multiply the demoniator by
it will be rational. if we multiply the demoniator by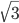 we must also multiply the numerators by
we must also multiply the numerators by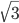 so that
so that
- Fractional indices may be used to express roots.
![x^{\frac{1}{n}}=\sqrt[n]{x}\:\:and\:\:x^{\frac{m}{n}}=(\sqrt[n]{x})^{m}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_5ef7209f3e2b6db6f5dc85d47769ca1f.gif)
- Make sure you can use your calculator to find powers and roots. The
 or
or ![\sqrt[x]{\:}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_e4f9329fefbc2a2a00d494554c49cb90.gif) button allows you to find roots.
button allows you to find roots.
For example:![\sqrt[5]{7776}=(7776)^{\frac{1}{5}}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_5425f3bfdda669025fcffce3f0418932.gif)
INDICES
- When the powers are fraction , then we can compare the indices in following manner.
for example :find which is greather or
or 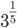
step-1 : find the L.C.M of the denominator of the fraction i.e 4,5 = 20
step-2 : find powers with the L.C.M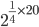 OR
OR  =
=  AND
AND 
step-3 : compare the result obtained in setp-2 : i.e as 32 < 81 we can say <
< 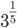
POINT TO REMEMBER
- Any none - zero real number raised to the power 0 equals 1
- I raised to any power is always 1.
 …….m times
…….m times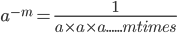
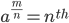 root of
root of 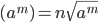
- If a
 1; A
1; A 0; a
0; a -1 and
-1 and  , then x = y
, then x = y - if
 then
then
- if x is odd, a=b
- if x is even, a=
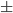 b
b




Important Examples - Surds and Indices
Question 1.What is the value of 
Solution: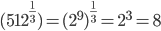


 The answer is 8+4+2=14
The answer is 8+4+2=14
Question 2.The product of  is equal to
is equal to
Solution: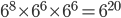
Question 3.The value of  is equal to
is equal to
Solution:
=
=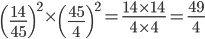
Question 4.If x=-5 and y=-6, then what is the value of  ?
?
Solution: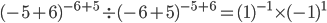
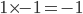
Question 5.In a cricket match, the number of runs scored by any team is equal to a power of the number of batsman playing in the team. Six batsman played in team A and eleven batsman played in team B. If team A won by 95 runs, then find the run scored by team A.
Solution: Let the power of the terms be x and y.
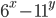 =95
=95
Put x =3, y= 2 (By trial and error)
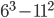 =95
=95
Hence satisfied
Score of team A= = 216
= 216
Note : These type of questions can be solved through answer choices.
POINTS TO REMEMBER
- The conjugate surd of

- To rationalize
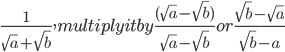
- If
 , then a=c and b=d
, then a=c and b=d - To find
 Write it in the form m+n+
Write it in the form m+n+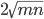 , such that m+n=a and 4mn=b, then
, such that m+n=a and 4mn=b, then 


- If
 =p, then p(p-1)=a
=p, then p(p-1)=a - The rationalizing factor of
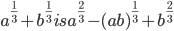
- The rationalize factor of

- The rationalize factor of

- The rationalize factor of

- The rationalize factor of
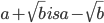
SOLVED EXAMPLES - Surds and Indices
Question 1.The value of  .
.
Solution : The given expression is in the form of

The exponent i.e.,  is in form of an infinite G.P
is in form of an infinite G.P
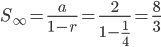
The given expression=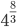
Question 2.Simplify 
Solution :By rationalizing 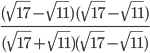
=
=
Question 3.If 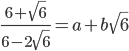 , then find the value of (a+2b)
, then find the value of (a+2b)
Solution : 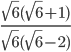
=
=
=


Question 4.What is the positive square root of 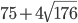 ?
?
Solution :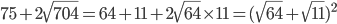
=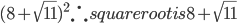
Question 5.Which of the following is the great ?

Solution :By squaring the values
=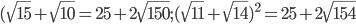
=
Since 25 is common to all the value, 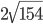 is the largest value.
is the largest value.
Hence 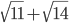 has the largest value.
has the largest value.
Surds and Indices Questions from Previous Year Exams
This test will cover Square, Cube, Indices and Surds syllabus of Bank Clerk Exam.


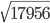


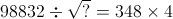
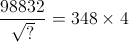
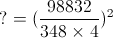
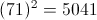
 = ?
= ?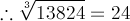
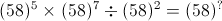
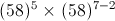
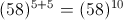



 is subtracted from the square of a number, the answer so obtained is 1893. What is the number?
is subtracted from the square of a number, the answer so obtained is 1893. What is the number?







 is subtracted from the square of a number, the answer so obtained is 10906. So that the number number is?
is subtracted from the square of a number, the answer so obtained is 10906. So that the number number is?







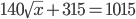
 +
+  = ?
= ?






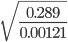
 is equal to ?
is equal to ?


 = 4040-559 = 3481
= 4040-559 = 3481



 Number =
Number =  - 7000
- 7000 is added to the square of a number, the answer so obtained is 28898. What is the number?
is added to the square of a number, the answer so obtained is 28898. What is the number?



















sqrt(2^5)=2*root(8)
sqrt(48)=2*root(12)
we get 2 as answer for question 10
option is not right selected to right answer because in question 10 option seceond 2 is right answer
Dear all, I really do like your little quiz, but unfortunately the answer you are suggesting to question #10 ("Bank PO 1990") is not correct. Instead of 4 - as suggested - the correct answer is 2. (Maybe you forgot to calculate SQRT(4) during simplification 🙂 )
Superb Knowledge is available with you but there are some blunders.Hope you will correct,Thank you so much.
nice pdf
help solve 5+2 root 6 all this into a square root =root2+root3