Square Root of a Number
The square root of a number is that number , the product of which by itself , is equal to the given number.
Important Example for Square Root and Cube Root
Example 1: The square root of x is denoted by 
Thus  etc.
etc.
Square Root of Factorization: When a given no is perfect square we resolve it in to prime factors and take the product of prime factors. choosing one out of every pair
Example 2: Given that  = 3.8729 evaluate
= 3.8729 evaluate 
Solution: 
= 
= =
= 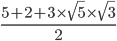
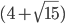 = 4+3.8729 = 7.8729
= 4+3.8729 = 7.8729
Example 3: if 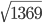 = 37 find the value of
= 37 find the value of 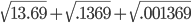
Solution: Given expression is , 
= = 3.7+0.37+0.037 = 4.107
= 3.7+0.37+0.037 = 4.107
Cube Root of a Number: The cube root of a number x is the number whose cube is x . we denote cube root of x by ![\sqrt[3]{x}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_6833f4eaccfb60d5c13fdf6b6cc30aef.gif)
Cube Root of Factorization: Resolve the given number in to prime factor and take the product of prime number .
thus ![\sqrt[3]{343}\; =\; \sqrt[3]{7\times 7\times 7}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_59640c60610a4d9996b8b64cf20190e8.gif) =7
=7
Square and Cube Root Previous Year Questions
Quiz-summary
0 of 28 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
Information
This test will cover Square, Cube, Indices and Surds syllabus of Bank Clerk Exam.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 28 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- Answered
- Review
-
Question 1 of 28
1. Question
1 points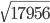 = ?Correct
= ?Correct
Given expression are :
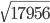 = ?
= ?=

=
 Incorrect
Incorrect
Given expression are :
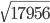 = ?
= ?=

=

-
Question 2 of 28
2. Question
1 points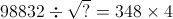 Correct
Correct
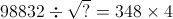
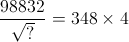
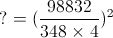
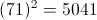 Incorrect
Incorrect
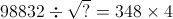
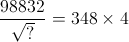
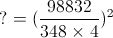
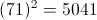
-
Question 3 of 28
3. Question
1 points = ?Correct
= ?Correct

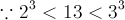 and last digit of number is 4
and last digit of number is 4
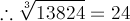 Incorrect
Incorrect

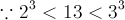 and last digit of number is 4
and last digit of number is 4
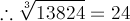
-
Question 4 of 28
4. Question
1 points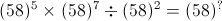 Correct
Correct
Incorrect
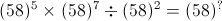
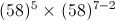
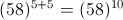
?=10 -
Question 5 of 28
5. Question
1 points Correct
Correct

 = 56 - 17 = 39Incorrect
= 56 - 17 = 39Incorrect

 = 56 - 17 = 39
= 56 - 17 = 39 -
Question 6 of 28
6. Question
1 pointsIf
 is subtracted from the square of a number, the answer so obtained is 1893. What is the number?Correct
is subtracted from the square of a number, the answer so obtained is 1893. What is the number?Correct
Incorrect

1893 + 29791 = 31684

-
Question 7 of 28
7. Question
1 points Correct
Correct


 Incorrect
Incorrect



-
Question 8 of 28
8. Question
1 points Correct
Correct
Incorrect

7 ( 625 + 450 + 324)
= 9793
-
Question 9 of 28
9. Question
1 pointsIf
 is subtracted from the square of a number, the answer so obtained is 10906. So that the number number is?Correct
is subtracted from the square of a number, the answer so obtained is 10906. So that the number number is?Correct


 Incorrect
Incorrect



-
Question 10 of 28
10. Question
1 points [Bank PO 1990]Correct
[Bank PO 1990]Correct
Incorrect
-
Question 11 of 28
11. Question
1 points Correct
Correct
Incorrect
-
Question 12 of 28
12. Question
1 points [Hotel Mgt 1993]Correct
[Hotel Mgt 1993]Correct
Incorrect
-
Question 13 of 28
13. Question
1 points Correct
Correct
Incorrect
-
Question 14 of 28
14. Question
1 points Correct
Correct
Incorrect
-
Question 15 of 28
15. Question
1 points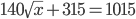 Correct
Correct
Incorrect
-
Question 16 of 28
16. Question
1 points +
+  = ?Correct
= ?Correct
 +
+  = ?
= ?
=>


56 + 64 = 120
Incorrect
 +
+  = ?
= ?
=>


56 + 64 = 120
-
Question 17 of 28
17. Question
1 points Correct
Correct


= 1000000 - 64000000 = 360000
 = 600Incorrect
= 600Incorrect


= 1000000 - 64000000 = 360000
 = 600
= 600 -
Question 18 of 28
18. Question
1 points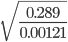 Correct
Correct
Incorrect
-
Question 19 of 28
19. Question
1 points is equal to ?Correct
is equal to ?Correct
Incorrect

-
Question 20 of 28
20. Question
1 points Correct
Correct
Incorrect

 = 4040-559 = 3481
= 4040-559 = 3481

-
Question 21 of 28
21. Question
1 points1617 + 2561 =
 Correct
Correct
Incorrect
4178 = 1369 +

 = 2089
= 2089

-
Question 22 of 28
22. Question
1 pointsWhat is the least number to be added to 7000 to make it a perfect square?
Correct
Incorrect

 Number =
Number =  - 7000
- 7000= 7056 - 7000 = 56
-
Question 23 of 28
23. Question
1 pointsIf
 is added to the square of a number, the answer so obtained is 28898. What is the number?Correct
is added to the square of a number, the answer so obtained is 28898. What is the number?Correct
Incorrect
Number =



-
Question 24 of 28
24. Question
1 pointsWhich number should replace both the questions marks (?) in the following equation?
 Correct
Correct
Incorrect
=>


=

-
Question 25 of 28
25. Question
1 points Correct
Correct
Incorrect


? = 9
-
Question 26 of 28
26. Question
1 points Correct
Correct
Incorrect

= 479.61
-
Question 27 of 28
27. Question
1 points Correct
Correct
Incorrect



? = 77
-
Question 28 of 28
28. Question
1 points Correct
Correct
Incorrect



Square and Cube Root Video Lecture

0 Comments