Sequences, following specific patterns are called progressions. Arithmetic progression (A.P). In this Chapter, besides discussing more about A.P.; arithmetic mean, geometric mean, relationship between A.M. and G.M., special series in forms of sum to n terms of consecutive natural numbers, sum to n terms of squares of natural numbers and sum to n terms of cubes of natural numbers will also be studied.
Sequences
Let the number of person’s ancestors for the first, second, third, ..., tenth generations are 2, 4, 8, 16, 32, ..., 1024. These numbers form what we call a sequence. Consider the successive quotients that we obtain in the division of 10 by 3 at different steps of division. In this process we get 3,3.3,3.33,3.333, ... and so on. These quotients also form a sequence. The various numbers occurring in a sequence are called its term . We denote the terms of a sequence by 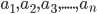 etc, the subscripts denote the position of the term. The
etc, the subscripts denote the position of the term. The  term is the number at the position of the sequence and is denoted by
term is the number at the position of the sequence and is denoted by  The
The  term is also called the general term of the sequence.
term is also called the general term of the sequence.
A sequence is called infinite, if it is not a finite sequence. For example, the sequence of successive quotients mentioned above is an infinite sequence, infinite in the sense that it never ends .Often, it is possible to express the rule, which yields the various terms of a sequencein terms of algebraic formula. Consider for instance, the sequence of even natural number 2, 4, 6,...
Here, 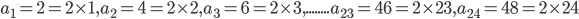 , and so on. In some cases, an arrangement of numbers such as 1, 1, 2, 3, 5, 8,.. has no visible pattern, but the sequence is generated by the recurrence relation given by.
, and so on. In some cases, an arrangement of numbers such as 1, 1, 2, 3, 5, 8,.. has no visible pattern, but the sequence is generated by the recurrence relation given by.

Above sequence is called Fibonacci sequence
Series
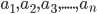 be a given sequence. Then, the expression
be a given sequence. Then, the expression s called the series associated with the given sequence. The series is finite or infinite according as the given sequence is finite or infinite. Series are often represented in compact form called sigma notation as means indicating the summation involved .Thus , the series
s called the series associated with the given sequence. The series is finite or infinite according as the given sequence is finite or infinite. Series are often represented in compact form called sigma notation as means indicating the summation involved .Thus , the series  is abbreviated . as
is abbreviated . as 
Note: When the series is used, it refers to the indicated sum not to the sum itself. For example, 1 + 3 + 5 + 7 is a finite series with four terms. When we use the phrase “ sum of a series,” we will mean the number that results from adding the terms, the
sum of the series is 16.
Arithmetic Progression (A.P)
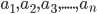 called arithmetic sequence or arithmetic progression if
called arithmetic sequence or arithmetic progression if  , where
, where is called the first term and the constant term d is called the common difference of the A.
is called the first term and the constant term d is called the common difference of the A.
Let us consider an A.P. (in its standard form) with first term a and common difference d , i.e., a , a + d, a+ 2d...,
Then the  term (general term) of the A.P. is
term (general term) of the A.P. is 
We can verify the following simple properties of an AP:
(i) If a constant is added to each term of an A.P., the resulting sequence is also an A.P.
(ii) If a constant is subtracted from each term of an A.P., the resulting sequence is also an A.P.
(iii) If each term of an A.P. is multiplied by a constant, then the resulting sequence is also an A.P.
(iv) If each term of an A.P. is divided by a non-zero constant then the resulting sequence is also an A.P.
Here, we shall use the following notations for an arithmetic progression :
a = the first term , l = the last term , d = common difference, n = the some of the series s _{n} = the sum to n terms of AP
Let a, a + d, a + 2d, ..., a + (n –1)dbe an A.P.
Then , l = a + (n– 1)d and ![s_{n}=\frac{n}{2}\left [2a+(n-1)d\right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f6eee7c90cd847518e47f38041472dcd.gif)
Arithmetic mean Given two numbers a and b. We can insert a number A between them so that a, A, bis an A.P. Such a number A is called the arithmetic mean (A.M.) of the numbers a and b. Note that, in this case, we have.
A – a = b – A , i.e  We may also interpret the A.M. between two numbers a and b as their average generally, given any two numbers a and b, we can insert as many numbers as we like between them such that the resulting sequence is an A.P. Let
We may also interpret the A.M. between two numbers a and b as their average generally, given any two numbers a and b, we can insert as many numbers as we like between them such that the resulting sequence is an A.P. Let 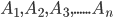 b is an A.P
b is an A.P
here, b is the  term , i.e, b = a+ [(n + 2) – 1] d = a+ (n + 1)d
term , i.e, b = a+ [(n + 2) – 1] d = a+ (n + 1)d
This gives 
Thus, n numbers between a and b are as follows:

Geometric Progression (G . P.)
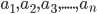 is called geometric progression , non zero and
is called geometric progression , non zero and 
By letting we obtain a geometric progression, a , ar ,
we obtain a geometric progression, a , ar , 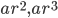 ........where a is called the first term and r is called the common ratio of the G.P.
........where a is called the first term and r is called the common ratio of the G.P.
As in case of arithmetic progression, the problem of finding the nth term or sum of n terms of a geometric progression containing a large number of terms would be difficult without the use of the formula which we shall develop in the next Section. We shall use the following notations with these formula: a = the first term, r = the common ratio, l = the last term
n = the numbers of terms, 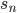 = the sum of last term
= the sum of last term
General term of a G .P. Let us consider a G.P. with first non-zero term ‘ a ’ and common ratio ‘ r.Write a few terms of it. The second term is obtained by multiplying a by r thus  = ar similarly, third term is obtained by multiplying
= ar similarly, third term is obtained by multiplying  by r thus
by r thus  , and so on
, and so on
Thus, a , G.P. can be written as 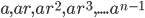 , according as G.P is finite or infinite , respectively . Thus the series
, according as G.P is finite or infinite , respectively . Thus the series  , are called finite or infinite geometric series , respectively.
, are called finite or infinite geometric series , respectively.
Sum to n terms of a G .P. Let the first term of a G.P. be a and the common ratio be r .
Let us denote by S the sum to first n terms of G.P.
Then
 , .............(1)
, .............(1)
Case 1: If r = 1, we have S n = a + a + a + ... + a (n terms) = na
case 2: If r ≠ 1, multiplying by r, we have
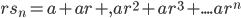 ,..............(2)
,..............(2)
Subtracting (1) and (2) , we get (1 - r) s_{n}=a-ar^{n}=a(1-r^{n}
This gives , 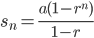
Geometric Mean (G .M)
The geometric mean of two positive numbers a and b is the number ab . Therefore, the geometric mean of 2 and 8 is 4. We observe that the three numbers 2,4,8 are consecutive terms of a G.P. This leads to a generalisation of the concept of geometric means of two numbers. Given any two positive numbers a and b , we can insert as many numbers as we like between them to make the resulting sequence in a G.P.
Let 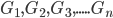 be n numbers between positive numbers a and b such that
be n numbers between positive numbers a and b such that  is a G.P . Thus b being
is a G.P . Thus b being  term , we have
term , we have

 ,
,  ,
,  ,
, 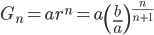
Relationship Between A.M. and G.M.: Let A and G be A.M. and G.M. of two given positive real numbers a
and b , respectively Thus we have A-G=
Thus we have

We obtain the relationship 
Sum to n Terms of Special Series
We shall now find the sum of first n terms of some special series, namely ;
1. 1 + 2 + 3 + ............+n (sum of first n natural numbers)
2. 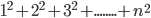 (sum of squares of the first n natural numbers)
(sum of squares of the first n natural numbers)
3.  (sum of cubes of the first n natural numbers).
(sum of cubes of the first n natural numbers).
Let us take them one by one:
(a). 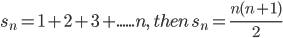
(b). 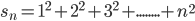
Point to be Remember
1. By a sequence , we mean an arrangement of number in definite order according to some rule. Also, we define a sequence as a function whose domain is the set of natural numbers or some subsets of the type {1, 2, 3, .... k}. A sequence containing a finite number of terms is called a finite sequence. A sequence is called infinite if it is not a finite sequence.2.
be the sequence, then the sum expressed as
is called series. A series is called finite series if it has got finite number of terms.
3. n arithmetic progression (A.P.) is a sequence in which terms increase or decrease regularly by the same constant. This constant is called common difference of the A.P. Usually, we denote the first term of A.P. by a , the common difference by d and the last term by l . The general term or the
term of the A.P. is given by
The sum Sn of the first n terms of an A.P. is given by
4. The arithmetic mean A of any two numbers a and b is given by
i.e the sequence a, A ,b is in A.P
5. A sequence is said to be a geometric progression or G. P., if the ratio of any term to its preceding term is same throughout. This constant factor is called the common ratio. Usually, we denote the first term of a G.P. by a and its common ratio by r. The general or the
term of G.P. is given by
.The sum
of the first n terms of G.P. is given by
6. The geometric mean (G.M.) of any two positive numbers a and bis given by
i.e the sequence a, G, b is GP .
Series Some Important Power
1.
2.
3.
4.
Progressions Questions from Previous Year Exams
progression

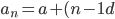
![s_{n}=\frac{n}{2}\left [ 2a+(n-1)d \right ]=\frac{n}{2}(a+l)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_7221e565a9a80f740f989d437852b8ad.gif)


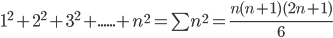








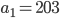
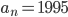


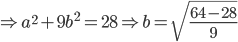



![s_{n}=\frac{n}{2}\left [ 2\times a_{x}+(n+1-2x)d \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_16c6c1433c7e00b61ff9cace6911bf6a.gif)


![s_{43}=\frac{43}{2}\left [ 2\times 2+(43-1)\times 4 \right ]=3698](https://questionpaper.org/wp-content/plugins/latex/cache/tex_574ab136d98f850ab3eefbd076466afb.gif)
![s_{n}=\frac{n}{2}\left [ 2a_{x}+(n-1)d\right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_05258bbb7b7faf5983abf6ec4d9d3ba3.gif)


![s_{10}=\frac{10}{2}\left [ 2\times 51+(10+1-20)\times3\right ]=375](https://questionpaper.org/wp-content/plugins/latex/cache/tex_6bd40b320b6083303f68f3f888294dc2.gif)

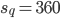


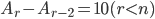



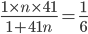
![s_{n}=\frac{n}{2}\left [ 1+97 \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_17ab3811d83c9433bcf39d2bbb5323cb.gif)
![s_{n}=\frac{n}{2}\left [ a+b \right ]\Rightarrow s_{7}=\frac{7}{2}\times 34\Rightarrow s_{7}=119](https://questionpaper.org/wp-content/plugins/latex/cache/tex_d82dc8e776ee0ed22693bebd8d4a2308.gif)
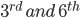



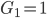


![s_{9}=\frac{1\times \left [ 1-(-3)^{9} \right]}{1-(-3)}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_c4cd0e83a641a4863e300faaa2ed6bae.gif)



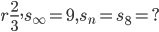
![s_{8}=9\times \left [ 1-(\frac{2}{3})^{8} \right ]=9\times \left [ 1-\frac{256}{6561} \right ]=\frac{6305}{729}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_72b75c8754d38a2444e51db590fad543.gif)



0 Comments