We studied about coordinate axes, coordinate plane, plotting of points in a plane, distance between two points, section formula, etc. All these concepts are the basics of coordinate geometry. Let us have a brief recall of coordinate geometry done in earlier classes. To recapitulate, the location of the points (6, – 4) and (3, 0) in the X-plane is shown in (Fig 10.1).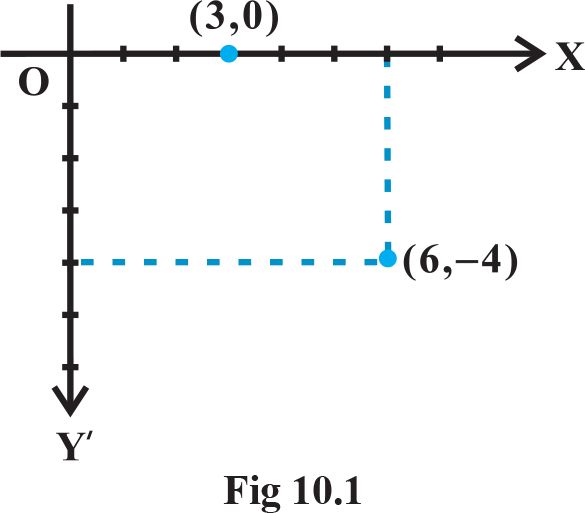
We may note that the point (6, – 4) is at 6 units distance from the y -axis measured along the positive x -axis and at 4 units distance from the X –axis measured along the negative Y-axis. Similarly, the point (3, 0) is at 3 units distance from the Y –axis measured along the positive X -axis and has zero distance from the X -axis. We also studied.
1. Distance between the points 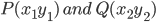

2. The coordinates of a point dividing the line segment joining the points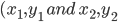 internally, in the ratio m: n are
internally, in the ratio m: n are 
Example: he coordinates of the point which divides the line segment joining A (1, –3) and B (–3, 9) internally, in the ratio 1: 3 are given by  and
and
3. In particular, if m=n ,the coordinate of the mid point of the line segment joining the point  . Are
. Are 
4. Area of the triangle whose vertices are 
Note : If the area of the triangle ABC is zero , then three point A,B and C lie on a line , i.e ,they are collinear .
We shall continue the study of coordinate geometry to study properties of the simplest geometry figure –straight line. Despite its simplicity , the line is a virtual concept of geometry. and enters into our daily experience in numerous interesting and useful ways. Main focus is on representing ,the slope is most essential.
Slope of a Line: A line in a coordinate plane forms two angles with the x-axis ,which are supplementary The angle (say)
Θ made by the line l with positive direction of x -axis and measured anti clockwise is called the inclination of the line. Obviously 0° ≤ θ ≤ 180° (Fig 10.2) .
We observe that lines parallel to x -axis, or coinciding with x -axis, have inclination of 0°. The inclination of a vertical line (parallel to or coinciding with y -axis) is 90°
Definition: If θ is the inclination of a line l , then tan θ is called the slope or gradient of the line l . The slope of a line those inclination is 90° is not defined. The slope of a line is denoted by m . Thus, m = tan θ, θ ≠ 90° It may be observed that the slope of x -axis is zero and slope of y -axis is not defined.
Slope of a Line when Coordinates of any two Points on the Line are given.
We know that a line is completely determined when we are given two points on it . Hence, we proceed to find the slope of a line in terms of the coordinates of two points on the line. Let 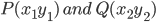 be two
be two
points on non-vertical line l whose inclination is θ . Obviously, x1 ≠x2 , otherwise the line will become perpendicular to
x -axis and its slope will not be defined. The inclination of the line l may be acute or obtuse. Let us take these two cases.
Draw perpendicular QR to x -axis and PM perpendicular to RQ as shown in Figs 10.3 (i) and (ii)
Case 1: When angle θ is acuten Fig 10.3 (i), ∠MPQ = θ. ... (1)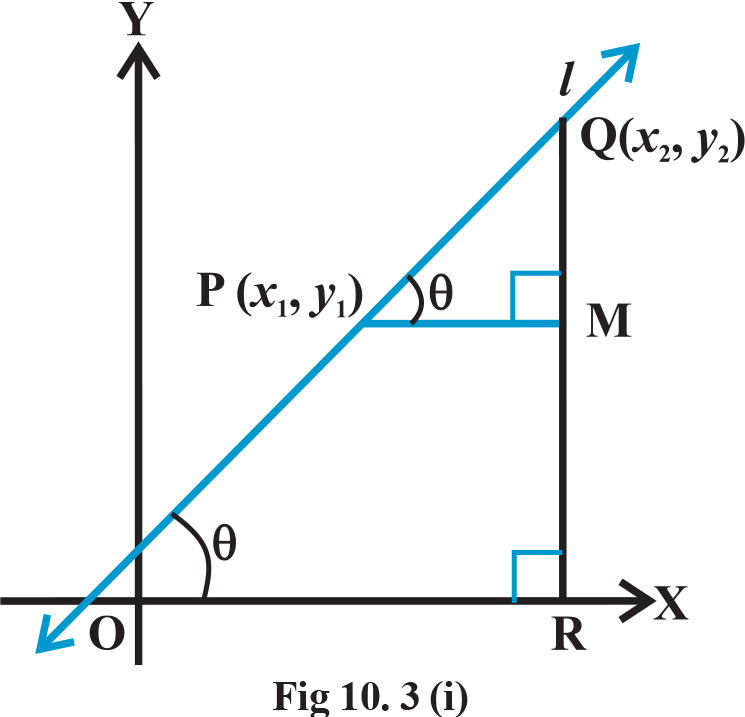
Therefore, slope of line l= m = tan θ.
But in ΔMPQ, we have tanθ = 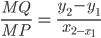 ..........(2)
..........(2)
From equations (1) and (2), we have,
When angle θ is obtuse: In Fig 10.3 (ii), we have ∠MPQ = 180° – θ.
Therefore, θ= 180° – ∠MPQ. Now, slope of the line l m= tan θ = tan ( 180° – ∠MPQ) = – tan ∠MPQ

Consequently, we see that in both the cases the slope m of the line through the points 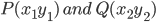 is given by
is given by 
Coordinate for Parallelism of Line in term of their Slope
In coordinate plane, suppose that non-vertical lines 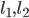 have slope
have slope 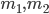
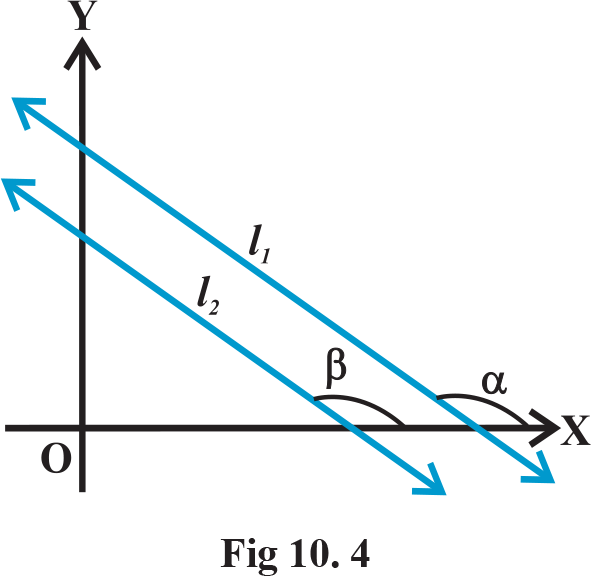 respectively. Let their inclinations be α and β , respectively
respectively. Let their inclinations be α and β , respectively
If the line 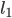 , (Fig 10.4) is parallel to
, (Fig 10.4) is parallel to  then their inclination are equal , i.e α = β , and hence, tan α= tan β
then their inclination are equal , i.e α = β , and hence, tan α= tan β
Therefore 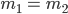 i.e., their slopes are equal. Conversely, if the slope of two lines
i.e., their slopes are equal. Conversely, if the slope of two lines 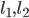 is same, i.e
is same, i.e 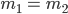 Then tan α = tan β.
Then tan α = tan β.
By the property of tangent function (between 0° and 180°), α = β.
Therefore, the lines are parallel. Hence, two non vertical lines 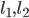 are parallel if and only if their slopes are equal.
are parallel if and only if their slopes are equal.
if the lines 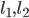 are perpendicular (Fig 10.5), then β = α + 90° . Therefore, tanβ= tan (α + 90°)
are perpendicular (Fig 10.5), then β = α + 90° . Therefore, tanβ= tan (α + 90°)
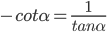 i.e
i.e 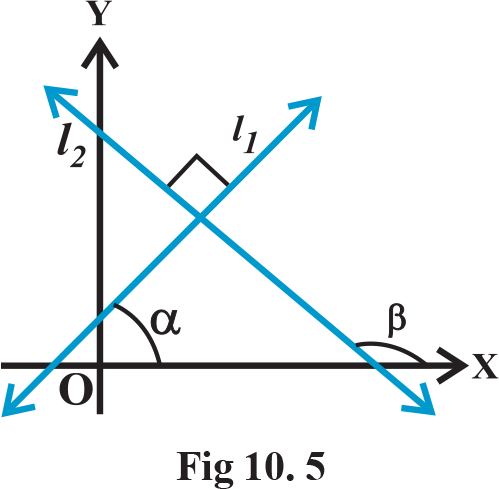
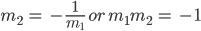 Conversely, if
Conversely, if  i.e., tan α tan β = – 1. Then tanα = – cot β = tan (β+ 90°) or tan (β– 90°)
i.e., tan α tan β = – 1. Then tanα = – cot β = tan (β+ 90°) or tan (β– 90°)
Therefore,α and β differ by 90°.Thus, lines 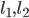 are perpendicular to each other.
are perpendicular to each other.
Hence, two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.
Angle between two Lines: When we think about more than one line in a
plane, then we find that these lines are either intersecting or parallel. Here we will 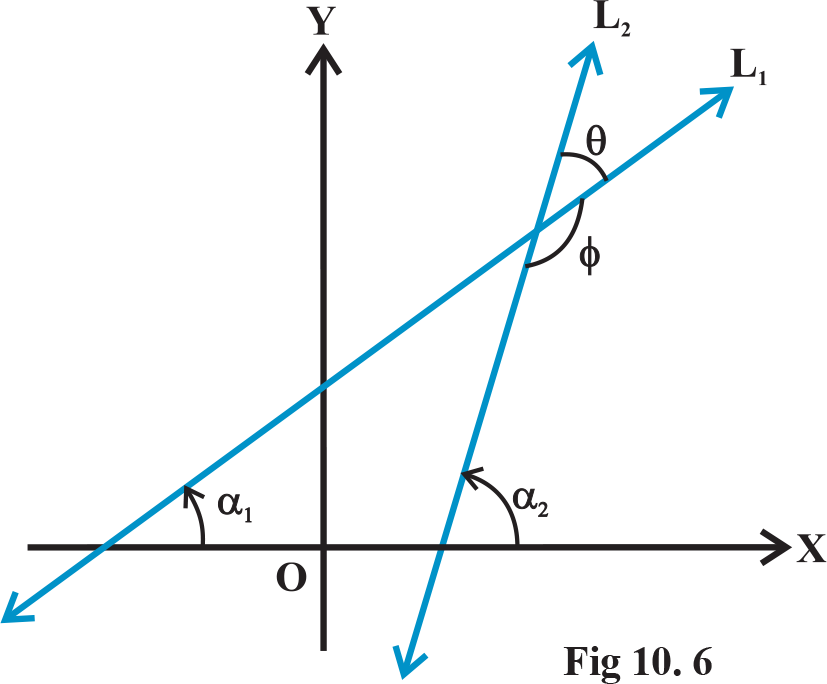
discuss the angle between two lines in terms of their slopes let , respectively.
respectively.
Then 
We know that when two lines intersect each other, they make two pairs of vertically opposite angles such that sum of any two adjacent angles is 180°. Let θ and φ be the adjacent angles between the lines
The 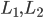 ,
,
Θ = α2– α1 and α1, α2 ≠ 90°.
Therefore 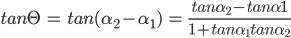 (as 1 + m1m2 ≠ 0) and φ = 180° – θ so that
(as 1 + m1m2 ≠ 0) and φ = 180° – θ so that 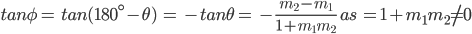
There Arise Two Cases :
case-1 : if 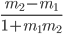 is positive, then tanθ will be positive and tan φ will be negative, which means θ will be acute and φ will be obtuse.
is positive, then tanθ will be positive and tan φ will be negative, which means θ will be acute and φ will be obtuse.
Case- 2: if 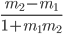 is negative, then tan θ will be negative and tan φwill be positive, which means that θ will be obtuse and φ will be acute.
is negative, then tan θ will be negative and tan φwill be positive, which means that θ will be obtuse and φ will be acute.
Thus, the acute angle (say θ) between lines . 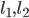 with slopes
with slopes 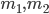 respectively, is given
respectively, is given 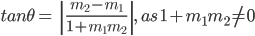 The obtuse angle (say φ) can be found by using φ=180 – θ
The obtuse angle (say φ) can be found by using φ=180 – θ
Various Forms of the Equation of a Line
We know that every line in a plane contains infinitely many points on it. This relationship between line and points leads us to find the solution of the following problem. How can we say that a given point lies on the given line? Its answer may be that or a given line we should have a definite condition on the points lying on the line. Suppose P (x, y) is an arbitrary point in the XY-plane and L is the given line. For the equation of L, we wish to construct a statement or condition for the point P that is true, when P is on L, otherwise false. Of course the statement is merely an algebraic equation involving the variables x and y. Now, we will discuss the equation of a line under different condition.
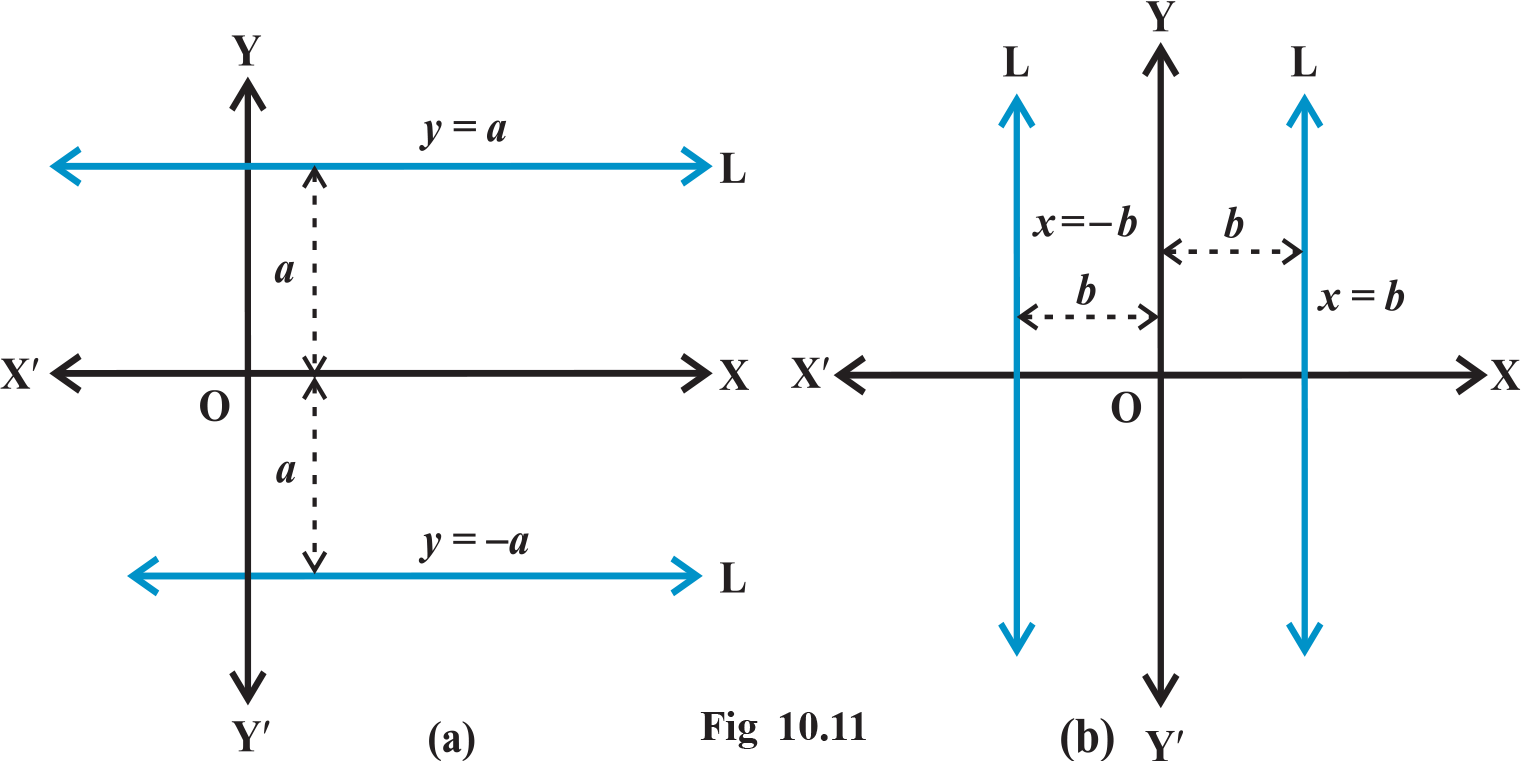
1. Horizontal and Vertical Lines If a horizontal line L is at a distance a from the x-axis then ordinate of every point lying on the line is either a or – a .Therefore, equation of the line L is either y = a or y = –a. Choice of sign will depend upon the position of the line according as the line is above or below the y-axis. Similarly ,the equation of a vertical line at a distance b from the y-axis is either x = b or x = -b (Fig 10.11)
2. Point-Slope Form Suppose that  is a fixed point on a non-vertical line L, whose slope is m . Let P (x, y) be an arbitrary point on L (Fig 10.13). Then, by the definition, the slope of L is given by
is a fixed point on a non-vertical line L, whose slope is m . Let P (x, y) be an arbitrary point on L (Fig 10.13). Then, by the definition, the slope of L is given by
 i.e
i.e 
Since the point  along with all point (x,y) on L satisfies 1) and no other point in the plane satisfies (1). Equation (1) is indeed the equation for the given line. Thus, the point (x, y) lies on the line with slope m through the fixed point if and only if, its coordinates satisfy the equation
along with all point (x,y) on L satisfies 1) and no other point in the plane satisfies (1). Equation (1) is indeed the equation for the given line. Thus, the point (x, y) lies on the line with slope m through the fixed point if and only if, its coordinates satisfy the equation 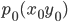

3. Two - Point Form : Let the line L passing through two given
points 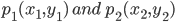 Let P ( x, y) be a general point on L (Fig 10.14) The three points
Let P ( x, y) be a general point on L (Fig 10.14) The three points  and P are collinear, therefore, we have slope of
and P are collinear, therefore, we have slope of  i.e ,
i.e , 
4. Slope Intersection Form : Sometimes a line is known to us with its slope and an intercept on one of the axes. We will now find equations of such lines.
Case I : Suppose a line L with slope m cuts the y-axis at a distance c from the origin (Fig 10.14). The distance c is called the y- intercept of the line L. Obviously, coordinates of the point where the line meet the y -axis are (0, c). Thus, L has slope m and passes through a fixed point (0, c ). Therefore, by point-slope form, the equation of L is.
Y –c = m(x-0) Thus, the point (x, y) on the line with slope m and y-intercept c lies on the line if and only if. y = mx + c
Case II: Suppose line L with slope m makes x- intercept d . Then equation of L is given y = m(x – d)
Students may derive this equation themselves by the same method as in Case .
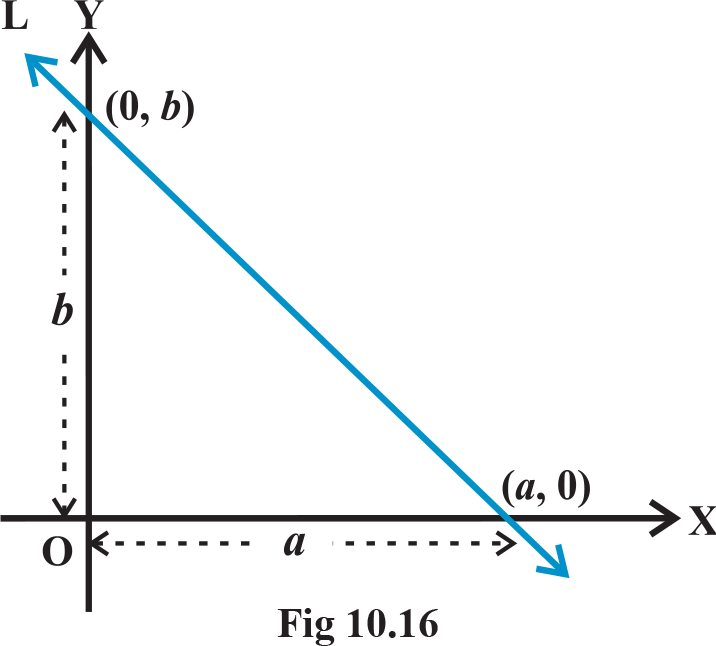
Intercept Form :Suppose a line L makes x -intercept a and y -intercept b on the axes. Obviously L meets x -axis at the point (a , 0) and y-axis at the point (0, b) (Fig 10.16). By two-point form of the equation of the line  or ay = -bx +ay i.e
or ay = -bx +ay i.e  Thus, equation of the line making intercepts a and b on x - and y -axis, respectively, is
Thus, equation of the line making intercepts a and b on x - and y -axis, respectively, is 
5. Normal Form: Suppose a non-vertical line is known to us with following data:(i) Length of the perpendicular (normal) from origin to the line.
(ii) Angle which normal makes with the positive direction of x-axis.
Let L be the line, whose perpendicular distance from origin O be OA = p and the angle between the positive x- axis and OA be ∠XOA = ω. The possible positions of line L in the Cartesian plane are shown in the Fig 10.17 . Now, our purpose is to find slope of L and a point on it. Draw perpendicular AM on the x -axis in each case. n each case, we have OM = p cosω and MA
= P sin ω , so that the coordinates of the point A are ( p cos ω, psin ω).
Further, line L is perpendicular to OA. Therefore

The slope of the line L = 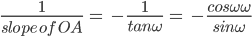
Thus, the line L has slope  and point
and point 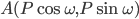 on it .Therefore, by point –slope form the equation of the line L is
on it .Therefore, by point –slope form the equation of the line L is

Hence, the equation of the line having normal distance p from the origin and angle ω which the normal makes with the positive direction of x –axis is given by x cos ω + y sinω = p
Note: We know, that the equation y = mx+ c, contains two constants, namely ,m and c. For finding these two constants, we need two conditions satisfied by the equation of line. In all the examples above, we are given two conditions to determine the equation of the line.
1. General Equation of a Line: n earlier classes, we have studied general equation of first degree in two variables
Ax + By + C = 0, where A, B and C are real constants such that A and B are not zero simultaneously. Graph of the equation Ax + By + C = 0 is always a straight line.
Therefore, any equation of the form A x + By + C = 0, where A and B are not zero simultaneously is called general linear equation or general equation of a line.
2. Different forms of Ax + By + C = 0The general equation of a line can be reduced into various forms of the equation of a line, by the following procedure.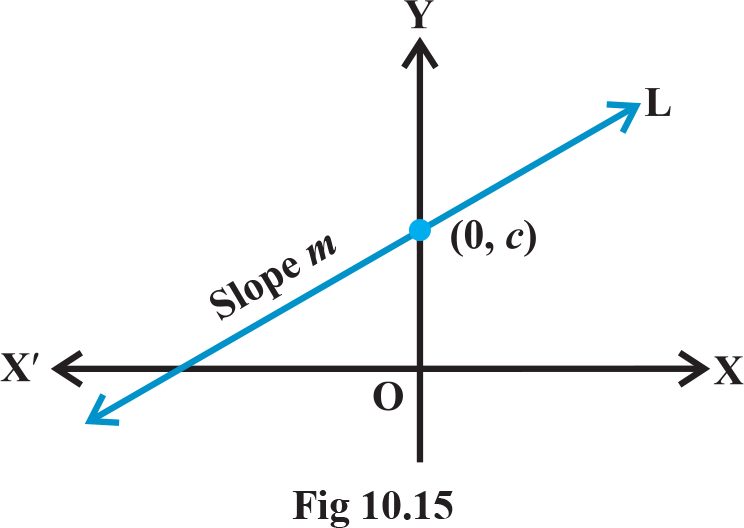
(a) Slope-Intercept Form If B ≠ 0, then Ax + By + C = 0 can be written as
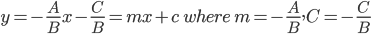
If B = 0 , then x =  ,which is a vertical line whose slope is undefined and x- intercept is
,which is a vertical line whose slope is undefined and x- intercept is
 ,
,
(b) Intercept Form: If C ≠0, then Ax +By + C = 0 can be written as .
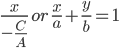
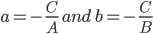
x -intercept is = and y- intercept is =
and y- intercept is =
If C = 0, then Ax + By + C = 0 can be written as Ax + By = 0, which is a line passing through the origin and, therefore, has zero intercepts on the axes
c. Normal form Let x cos ω+ y sin ω= p be the normal form of the line represented by the equation Ax + By + C = 0 or
Ax +By = – C. Thus, both the equations are same and therefore , 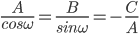
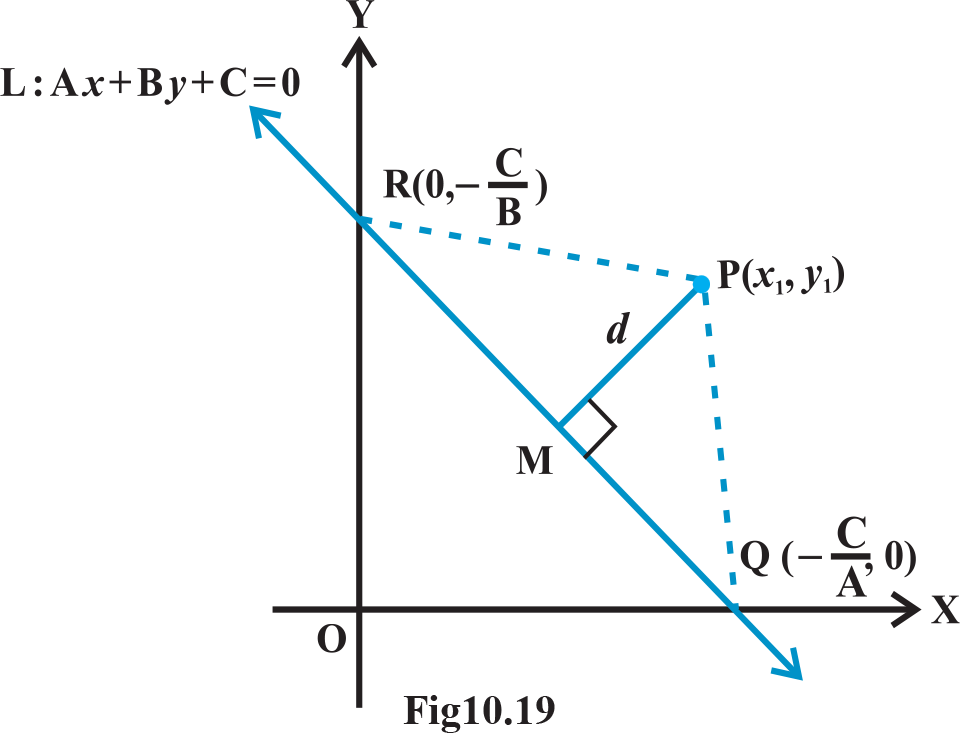
Distance of a Point From a Line: The distance of a point from a line is the length of the perpendicular drawn from the point to the line. Let L: Ax+ By + C = 0 be a line, whose distance from the point 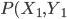 Draw a perpendicular PM from the point P to the line L (Fig 10.19)If the line meets the x- and y- axes at the points Q and R, respectively. Then, coordinates of the points are
Draw a perpendicular PM from the point P to the line L (Fig 10.19)If the line meets the x- and y- axes at the points Q and R, respectively. Then, coordinates of the points are 
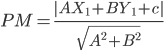
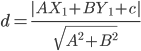
Points to Remember
1. Slope(m) of a non-vertical line passing through the points 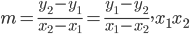
2. f a line makes an angle á with the positive direction of x -axis, then the slope of the line is given by m = tan α, α ≠ 90
3. Slope of horizontal line is zero and slope of vertical line is undefined
4. An acute angle (say θ) between lines 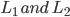 with slopes
with slopes given by
given by

5. wo lines are parallelif and only if their slopes are equal.
6. Two lines are perpendicular if and only if product of their slopes is –1.
7. Three points A, B and C are collinear, if and only if slope of AB = slope of BC.
8. Equation of the horizontal line having distance a from the x -axis is either y = a or y = – a.
9. Equation of the vertical line having distance b from the y -axis is either x = b or x = –b
10. The point (x, y ) lies on the line with slope m and through the fixed point 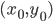 if and only if its coordinates satisfy the equation
if and only if its coordinates satisfy the equation 
11. Equation of the line passing through the point is given by
is given by

12. The point (x, y) on the line with slope m and y-intercept c lies on the line if and only if y = mx + c
13 . If a line with slope m makes x- intercept d. Then equation of the line is y = m(x– d).
14. Equation of a line making intercepts a and b on the x-and y-axis. respectively , is 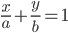
15. The equation of the line having normal distance from origin p and angle between normal and the positive x -axis 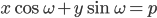
16. Any equation of the form Ax + By + C = 0, with A and B are not zero, simultaneously, is called the general linear equation or general equation of a line .
17 . The perpendicular distance (d) of a line Ax + By+ C = 0 from a point 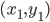 is given by
is given by 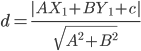
18. Distance between the parallel lines 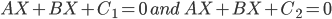 is given by d
is given by d
Then 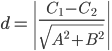
Coordinate Geometry Important Questions
co-ordinate geometry








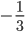


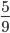
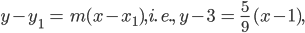
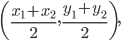
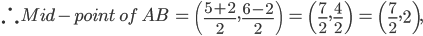




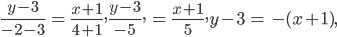




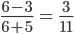


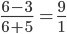








0 Comments