Calculus is that branch of mathematics which mainly deals with the study of change in the value of a function as the points in the domain change. First, we give an intuitive idea of derivative (without act actually defining it). Then we give a naive definition of limit and study some algebra of limits. Then we come back to a definition of derivative and study some algebra of derivatives. We also obtain derivatives of certain standard function.
Limits: The above discussion clearly points towards the fact that we need to understand limiting process in greater clarity. We study a few illustrative examples to gain some familiarity with the concept of limit . Consider the function f(x ) =  bserve that as x takes values very close to 0, the value of f ( x ) also moves towards 0.
bserve that as x takes values very close to 0, the value of f ( x ) also moves towards 0.
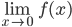
In genral as 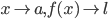 , then l is called limit of the function f(x) which is symbolically written as
, then l is called limit of the function f(x) which is symbolically written as 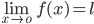 .
.
Consider the following function g(x) = |x| , x  . observer that g(0) is not defined. Computing the value of g(x) for the value of x very near to 0 we see that the value of g (x) moves towards zero .
. observer that g(0) is not defined. Computing the value of g(x) for the value of x very near to 0 we see that the value of g (x) moves towards zero .
So,  .
.
This intuitively clear from the graph of y = |x | for x ≠ 0
Note : we say 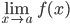 is the expected value of f at x = a given the values of f near x to the left of a. This value is called the left hand limit of f at a.
is the expected value of f at x = a given the values of f near x to the left of a. This value is called the left hand limit of f at a.
We say 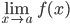 is the expected value of f at x = a given the values of f near x to the left of a. This value is called the right hand limit of of f(x) at a if the right and left limit coincide , we call common value as the limit of f(x) at x = a and denote it by
is the expected value of f at x = a given the values of f near x to the left of a. This value is called the right hand limit of of f(x) at a if the right and left limit coincide , we call common value as the limit of f(x) at x = a and denote it by 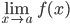
Algebra of limit
Theorem 1: Let f and g be two functions such that both  exist then.
exist then.
- Limit of sum of two functions is sum of the limits of the function :
![\lim_{x\rightarrow a}[f(x)+g(x)]=\lim_{x\rightarrow a}f(x)+\lim_{x\rightarrow 0}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_efbab1c105d8c7d9a2ab6f0cf2a55022.gif)
- Limit of difference of two functions is difference of the limits of the functions, i.e
![\lim_{x\rightarrow a}[f(x)-g(x)]=\lim_{x\rightarrow a}f(x)-\lim_{x\rightarrow 0}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_c8f2f47bb7eaa0567442cae8eaaec089.gif)
- Limit of product of two functions is product of the limits of the functions, i.e
![\lim_{x\rightarrow a}[f(x)\cdot g(x)]=\lim_{x\rightarrow a}f(x)\cdot\lim_{x\rightarrow 0}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_4699dade227ee1253ffcfb66224cd595.gif)
- Limit of quotient of two functions is quotient of the limits of the functions (whenever the denominator is non zero) , i .e

Note: In particular as case of (iii), when g is the constant function such that g(x) = λ , for some real number λ ,
we have
Limits of polynomials and rational function:
A function f is said to be a polynomial function if f(x) is zero function or if  , where
, where  are real numbers such that a n ≠ 0 for some natural numbers n.
are real numbers such that a n ≠ 0 for some natural numbers n.
We know that 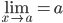 Hence
Hence 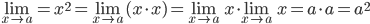
Or 
A function f is said to be a rational function if  are polynomial such that
are polynomial such that  Then ,
Then ,

Limit of trigonometric function : Let f and g be two real valued functions with the same domain such that f (x) ≤ g(x) for all x in the domain of definition, For some a, if both  . in fig 13.8
. in fig 13.8
Theorem:
The following are two important limits
Example: Evaluate 
Solution: ![\lim_{x\rightarrow 0}\frac{\sin4 x}{2x}=\lim_{x\rightarrow 0}\left [ \frac{sin4x}{4x}\cdot \frac{2x}{sin2x}\cdot 2 \right ]= 4\lim_{x\rightarrow 0}\left [ \frac{\sin4x}{4x}\right ]\div \left [ \frac{\sin 2x}{2x} \right ]= 2\lim_{4x\rightarrow 0}\left [ \frac{\sin4x}{4x}\right ]\div \lim_{2x\rightarrow 0}\left [ \frac{\sin 2x}{2x} \right ]=2\times 1\times 1=2\left (as\: x\rightarrow 0,4x\rightarrow 0,\: and\: 2x\rightarrow 0 \right )](https://questionpaper.org/wp-content/plugins/latex/cache/tex_6cf62df42b74d79f6bfb52cc45cc6cae.gif)
Derivatives: uppose f is a real valued function and a is a point in its domain of definition. The derivative of f at a is defined by 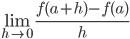
provided this limit exists. Derivative of f (x)at a is denoted by f ′(a). observe that f′ (a) quantifies the change in f(x) at a with respect to x.
Example: Find the derivative at x = 2 of the function f (x) = 3x.
Solution: 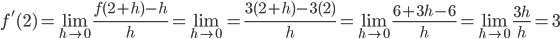 The derivative of the function 3x at x = 2 is 3 .
The derivative of the function 3x at x = 2 is 3 .
Algebra of derivative of functions: Since the very definition of derivatives involve limits in a rather direct fashion, we expect the rules for derivatives to follow closely that of limits. We collect these in the following theorem .
Theorem
- Derivative of sum of two functions is sum of the derivatives of the function.
![\frac{\mathrm{d} }{\mathrm{d}x}\left [ f(x)+g(x) \right ]=\frac{\mathrm{d} }{\mathrm{d} x}f(x)+\frac{\mathrm{d} }{\mathrm{d} x}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_fe6e46d1ce7a96da7a4855d2a21dc719.gif)
- Derivative of difference of two functions is difference of the derivatives of the function.
![\frac{\mathrm{d} }{\mathrm{d}x}\left [ f(x)-g(x) \right ]=\frac{\mathrm{d} }{\mathrm{d} x}f(x)-\frac{\mathrm{d} }{\mathrm{d} x}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f9ccde7c2bddb3ff69fb76dbdfe4e947.gif)
- Derivative of product of two functions is given by the following product rule.
![\frac{\mathrm{d} }{\mathrm{d}x}\left [ f(x).g(x) \right ]=\frac{\mathrm{d} }{\mathrm{d} x}f(x).\frac{\mathrm{d} }{\mathrm{d} x}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_90b8e1d9313cb085dcebe2d63a7798a3.gif) .
. - Derivatives of quotient of two function is given by the following rules (whenever the dimension is non -zero )
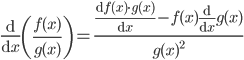
Derivatives of 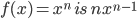 for any positive integer n . By definition we have
for any positive integer n . By definition we have

Derivatives of polynomial trigonometric functions : We start with the following theorem which tells us the derivative of a polynomial function .
Example: Let  We use the quotient rule on this function whereve.
We use the quotient rule on this function whereve.

Points to be Remember:
- The expected value of the function as dictated by the points to the left of a point defines the left hand limit of the function at that point. Similarly the right hand limit .
- Limit of a function at a point is the common value of the left and right hand limit if they coincide.
- For a function f and a real number a ,
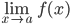 and f(a) may not be same (in fact , one may be define and not other one )
and f(a) may not be same (in fact , one may be define and not other one ) - For function f and g the following hold:
![\lim_{x\rightarrow a}[f(x)+g(x)]=\lim_{x\rightarrow a}f(x)+\lim_{x\rightarrow 0}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_efbab1c105d8c7d9a2ab6f0cf2a55022.gif)
![lim_{x\rightarrow a}[f(x)-g(x)]=\lim_{x\rightarrow a}f(x)-\lim_{x\rightarrow 0}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f77f70d14b5ac2bff90a51c5549e3ec8.gif)
![\lim_{x\rightarrow a}[f(x)\cdot g(x)]=\lim_{x\rightarrow a}f(x)\cdot\lim_{x\rightarrow 0}g(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_4699dade227ee1253ffcfb66224cd595.gif)

- Following are some of the standard limit



- The derivative of a function f at a is defined by
by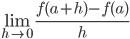
- Derivative of a function f at any point x is defined by
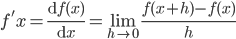
- For functions u and v the following holds
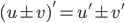
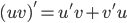
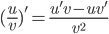 provided all are defined .
provided all are defined . - Following are the some of the standard derivatives .
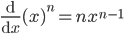


Differentiability
Derivatives of composite function:
Example: find the derivative of f, where
Solution: ![\frac{d}{dx}f(x)= \frac{d}{dx}\left [ (2x+1)^{3}\right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_361c081c89b802b79be8fc41b5aa1b17.gif)



Now, observe that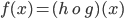
Where g(x) =2x+1 , and  .put t = g(x)=2x +1.Then f (x) = h(t) =
.put t = g(x)=2x +1.Then f (x) = h(t) =  .Thus
.Thus

Derivatives of Functions in Parametric Forms: Some times the relation between two variables is neither explicit nor implic, but some link of a third variable with each of the two variables, separately , establishes a relation between the first two variables. In such a situation, we say that the relation between them is expressed via a third variable. The third variable is called the parameter . More precisely, a relation expressed between two variables x and y in the form x = f(t), y= g(t) is said to be parametric form with t as a parameter.
In order to find derivative of function in s uch form, we have by chain rule:

Thus , 
Points to be Remember :
- A real valued function is continuous at a point in its domain if the limit of the function at that point equals the value of the function at that point. A function is continuous if it is continuous on the whole of its domain .
- Sum, difference, product and quotient of continuous functions are continuous. i.e., if f and g are continuous functions, then
 is continuous .
is continuous .
(f. g) (x) = f(x) . g(x) is continuous
 (where g(x) ≠ 0) is continuous ) .
(where g(x) ≠ 0) is continuous ) .- Every differentiable function is continuous, but the converse is not true.
- Chain rule is rule to differentiate composites of functions. If f = v o u , t = u(x) and if both
 exist then
exist then
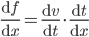
- Following are some of the standard derivatives (in appropriate domains):
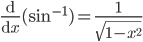




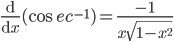


- Logarithmic differentiation is a powerful technique to differentiate functions of the form
![f(x)=\left [ u(x) \right ]^{v(x)}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_0396151e63e388a734879e11ee3f0c78.gif) Here both f (x) and u(x) need to be positive for this technique to make sense.
Here both f (x) and u(x) need to be positive for this technique to make sense. - Rolle’s Theorem : If f: [a, b] →R is continuous on [a, b] and differentiable on (a, b) such that f(a) = f(b), then There exists some c in (a, b) such that f′(c) = 0.
- Mean Value Theorem: If f: [a, b] →R is continuous on [a, b] and differentiable on (a, b). Then there exists some c in (a, b) such that

- Second derivatives test : Let f be a function defined on an intervalI and c ∈ I. Let f be twice differentiable at c. Then
(i) x = c is a point of local maxima if f′(c) = 0 and f′′(c) < 0The values f(c) is local maximum value of f . (ii) x = c is a point of local minima if f′(c) = 0 and f′′(c) > 0 In this case, f (c) is local minimum value of f .
(iii) The test fails if f′(c) = 0 and f′′(c) = 0.In this case, we go back to the first derivative test and find whether
C is a point of maxima, minima or a point of inflexion. - Working rule for finding absolute maxims and/or absolute minims
Step 1: Find all critical points of f in the interval, i.e., find points x where either f′(x) = 0 or f is not differentiable.
Step 2 : Take the end points of the interval.
Step 3 : At all these points (listed in Step 1 and 2), calculate the values of f.
Step 4 : Identify the maximum and minimum values of f out of the values calculated in Step 3. This maximum value will be the absolute maximum value of f and the minimum value will be the absolute minimum value of f .
Integration
- Let
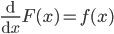 . Then we write
. Then we write These integrals are called indefinite integrals or general integrals, C is called constant of integration. All these integrals differ by a constant
These integrals are called indefinite integrals or general integrals, C is called constant of integration. All these integrals differ by a constant - From the geometric point of view , an indefinite integral is collection of family of curves, each of which is obtained by translating one of the curves parallel to itself upwards or downwards along the y -axis.
- Some properties of indefinite integrals are as follows
![\int \left [ f(x) +g(x)\right ]=\int f(x)dx+\int g(x)dx](https://questionpaper.org/wp-content/plugins/latex/cache/tex_6bdba617d378c690e23d9112e3fe3c9e.gif)
- For any real number k,

More generally if are function and
are function and 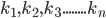 are real numbers .
are real numbers . ![\int \left [ k_{1}f_{1}(x) +k_{2}f_{2}(x)\right ]+.......+\int\left [ k_{n}f_{n}(x) \right ]dx=k_{1}\int f_{1}(x)dx+k_{2}\int f_{2}(x)dx+.....+k_{n}\int f_{n}xdx](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f0751b18ed60bbaec40402bf3e887829.gif)
Some Standard Integral:
 . Particularly
. Particularly 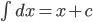
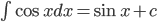


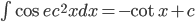





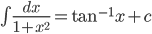


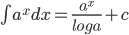
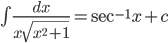
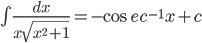
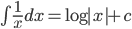
- Integration by partial fractions:
Recall that a rational function is ratio of two polynomials of the form , where P(x) and Q(x) are polynomials in
where P(x) and Q(x) are polynomials in
X and Q(x) ≠ 0. If degree of the polynomial P(x) is greater than the degree of the polynomial Q(x), then we may divide p(x) by q(x) so
that 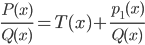 where T (x) is a polynomial in x and degree of P1(x) is less than the degree of Q(x). T(x) being polynomial can be easily integrated.
where T (x) is a polynomial in x and degree of P1(x) is less than the degree of Q(x). T(x) being polynomial can be easily integrated. 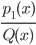 can be integrated by expression
can be integrated by expression 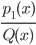 as the sum of partial fraction of the following type:
as the sum of partial fraction of the following type:
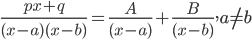



 ,
,
Where , x^{2}+bx+c can not be factorised further.- Integration by substitution:
A change in the variable of integration often reduces an integral to one of the fundamental integrals. The method in which we change the variable to some other variable is called the method of substitution. When the integrand involves some trigonometric functions, we use some well known identities to find the integrals. Using substitution technique, we obtain the following standard integrals. 



- Integrals of some special functions:




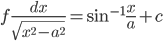
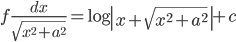
- Integration by parts:
For given function is we have
we have
![\int f_{1}(x)\cdot f_{2}(x)dx=f_{1}(x)\int f_{2}xdx-\int \left [ \frac{\mathrm{d} }{\mathrm{d} x}f_{1}(x)\cdot \int f_{2}(x)dx \right ]dx](https://questionpaper.org/wp-content/plugins/latex/cache/tex_dae9ddba31ce4602e9d591ef1490dd7e.gif) , i.e The integral of the product of two functions = first function × integral of the second function – integral of {differential coefficient of the first function × integral of the second function}. Care must be taken in choosing the first function and the second function. Obviously , we must take that function as the second function whose integral is well known to us.
, i.e The integral of the product of two functions = first function × integral of the second function – integral of {differential coefficient of the first function × integral of the second function}. Care must be taken in choosing the first function and the second function. Obviously , we must take that function as the second function whose integral is well known to us.
![\int \left [ e^{x}f(x)+f'(x)\right ]=\int e^{x}f(x)dx+c](https://questionpaper.org/wp-content/plugins/latex/cache/tex_c2fdaf1da6e0c24beb89361f7163be9b.gif)
- Integrals of the type
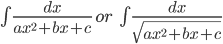 can be transformed in to standard form by expressing
can be transformed in to standard form by expressing
![ax^{2}+bx+c=a\left [ x^{2}+\frac{a}{b}x+\frac{c}{a}\right ]=a\left [ \left ( x+\frac{b}{2a} \right )^{2}+\left ( \frac{c}{a}-\frac{b^{2}}{4a^{2}} \right )\right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_7b6f0c3446123112b52e11ddf65a5817.gif)
- Integral of the type:
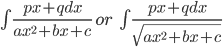 can be transformed in to standard form by expressing
can be transformed in to standard form by expressing

Where A and B are determined by comparing coefficients on both sides - First fundamental theorem of integral calculus: Let the area function be defined by A(x) =
 or all x ≥ a, where the function f is assumed to be continuous on [a, b]. Then A′(x) = f(x) for all x∈[a, b]
or all x ≥ a, where the function f is assumed to be continuous on [a, b]. Then A′(x) = f(x) for all x∈[a, b] - Second fundamental theorem of integral calculus Let f be a continuous function of x defined on the closed interval [a, b] and let F be the function such that
 for all x in the domain of f, then
for all x in the domain of f, then ![\int_{a}^{b}f(x)dx=[F(x)+c]_{a}^{b}=F(b)-F(a)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_09037694b7bf7d811f21f7807454fdf6.gif)
This is called the definite integral of f over the range [a, b], where a and bare called the limits of integration,
a being the lower limit and b the upper limit.
Calculus Important Questions
calculas
Calculus Important Videos - Must Watch

![\lim_{x\rightarrow a}[(\lambda ,f)(x)]=\lambda \lim_{x\rightarrow a}f(x)](https://questionpaper.org/wp-content/plugins/latex/cache/tex_3706e97a34ab2780117766a01264743d.gif)
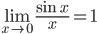




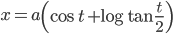

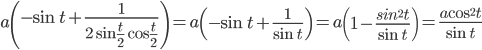

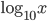




![\frac{\mathrm{d} y}{\mathrm{d} x}=f'\left ( \frac{2x-1}{x^{2}+1} \right )\cdot \left [ \frac{(x^{2}+1))2-(2x-1)\cdot 2x}{(x^{2}+1)^{2}} \right ]=\sin \left ( \frac{2x-1}{x^{2}+1} \right )^{2}\cdot \left [ \frac{2+2x-2x^{2}}{(x^{2}+1)^{2}} \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_39f8833b7aa5bfde210d296ce6bac146.gif)
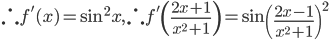


![\sum_{r=1}^{x}\left [ \tan^{-1}(r+1)-\tan^{-1}r\right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_6f8fa3e5053acc424212dd42d824ff3b.gif)
![\left [ \tan^{-1}2-\tan^{-1}1+\tan^{-1}3-\tan^{-1}2+..+\tan^{-1}x-\tan^{-1}(x-1)+\tan^{-1}(x+1)-\tan^{-1}x \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_0218ad005018cd0327e5bb4e671032dc.gif)
![\left [ \tan^{-1}(x+1)-\tanh^{-1}x \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f4ec9afa4c56bb206b0f1c6c5cad2d50.gif)



![\lim_{x\rightarrow 0}\left [n+ \frac{n(n-1)}{1.2}x+....+x^{^{n-1}} \right ]=n](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f70ccc2f5d04cc9d7d9643758d885627.gif)


![\lim_{x\rightarrow 0}\frac{\sqrt[5]{1+3x^{4}}-1}{x}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f363d0b057dbc8b291dca36ee0524d77.gif)
![\lim_{x\rightarrow 0}\frac{\sqrt[5]{1+3x^{4}}-1}{x}=\lim_{x\rightarrow 0}\frac{1+3x^{4}-1}{\left ( (\sqrt[5]{1+3x^{4})^{4}+(\sqrt[5]{1+3x^{4})^{3}+(\sqrt[5]{1+3x^{4})^{2}+\sqrt[5]{1+3x^{1})^{4}} \right )}=\frac{0}{5}=0](https://questionpaper.org/wp-content/plugins/latex/cache/tex_e1b3f5d7c1fabcd067a82de8d3a9d249.gif)
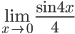
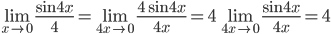



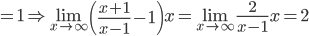


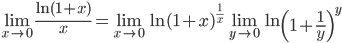

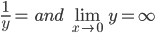



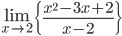





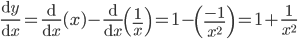

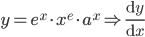







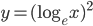
![\left [ Let\: u=\log_{e}x \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_6c63c8506f86852d901f4ce07fedcf63.gif)

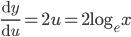
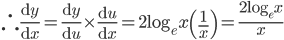


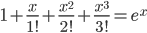
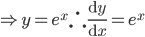

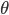
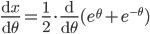

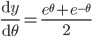









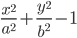


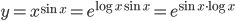
![\therefore \frac{\mathrm{d} y}{\mathrm{d} x}=e^{\sin x\cdot \log x}\left [\sin x\cdot \frac{1}{x} +\log x\cdot \cos x \right ]=x^{\sin x}\left ( \frac{\sin x}{x}+\log x\cos x \right )](https://questionpaper.org/wp-content/plugins/latex/cache/tex_15978369c73934b6500467ef444cbfb8.gif)

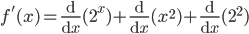
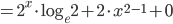
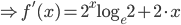
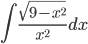
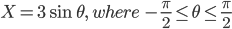



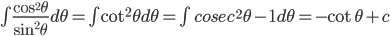




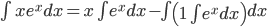
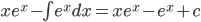




![\int \left [ \sin (\log x)+\cos (\log x) \right ]dx](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f64710a17b259efeef80dfc4f479c561.gif)
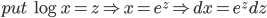
![\therefore \int \left [ \sin (\log x)+\cos (\log x) \right ]dx=\int e^{z}\left ( \sin z+\cos z\right )dz](https://questionpaper.org/wp-content/plugins/latex/cache/tex_a59f8ae676000f86955274cc9dae1c94.gif)


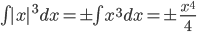

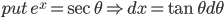
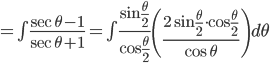






0 Comments