However, for higher powers like  , etc., the calculations become difficult by using repeated multiplication. This difficulty was overcome by a theorem known as binomial theorem. It gives an easier way to expand ,
, etc., the calculations become difficult by using repeated multiplication. This difficulty was overcome by a theorem known as binomial theorem. It gives an easier way to expand ,  where n is an integer o r a rational number.
where n is an integer o r a rational number.
Binomial Theorem for Positive Integral Indices
Let us have a look at the following identities done earlier
 a + b ≠ 0
a + b ≠ 0




In these expansions, we observe that
- The total number of terms in the expansion is one more than the index. For example, in the expansion of
 , number of terms is 3 whereas the index of
, number of terms is 3 whereas the index of  , is 2
, is 2 - Powers of the first quantity ‘ a ’ go on decreasing by 1 whereas the powers of the second quantity ‘ b ’ increase by 1, in the successive terms.
- In each term of the expansion, the sum of the indices of a and b is the same and is equal to the index of a + b
We now arrange the coefficients in these expansions as follows (Fig8.1):

Do we observe any pattern in this table that will help us to write the next row? Yes we do. It can be seen that the addition of 1’s in the row for index 1 gives rise to 2 in the row for index 2. The addition of 1, 2 and 2, 1 in the row for index 2, gives rise to 3 and 3 in the row for index 3 and so on. Also, 1 is present at the beginning and at the end of each row. This can be continued till any index of our interest.
We can extend the pattern given in Fig 8.2 by writing a few more rows.
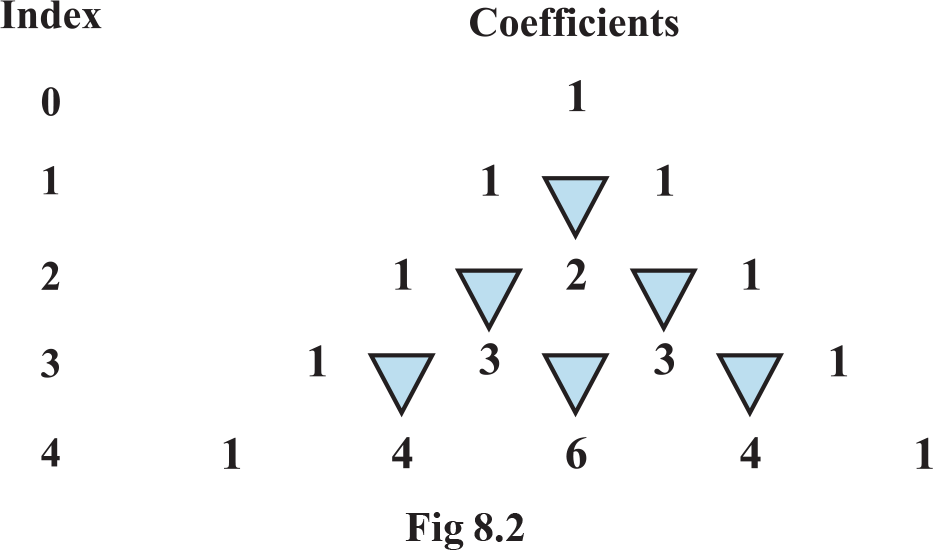
Pascal’s Triangle
The structure given in Fig 8.2 looks like a triangle with 1 at the top vertex and running down the two slanting sides. This array of numbers is known as Pascal’s triangle , after the name of French mathematician Blaise Pascal. It is also known as Meru Prastara by Pingla.
Expansions for the higher powers of a binomial are also possible by using Pascal triangle . let us expand
by using Pascal’s triangle. The row for index 5 is 1 5 10 10 5 1
Using this row and our observations (i), (ii) and (iii), we get

Now, if we want to find the expansion of  , we are first required to get the row for index 12. This can be done by writing all the rows of the Pascal’s triangle till index 12. This is a slightly lengthy process. The process, as you observe, will become more difficult, if we need the expansions involving still larger powers. We thus try to find a rule that will help us to find the expansion of the binomial for any power without writing all the rows of the Pascal’s triangle, that come before the row of the desired index.
, we are first required to get the row for index 12. This can be done by writing all the rows of the Pascal’s triangle till index 12. This is a slightly lengthy process. The process, as you observe, will become more difficult, if we need the expansions involving still larger powers. We thus try to find a rule that will help us to find the expansion of the binomial for any power without writing all the rows of the Pascal’s triangle, that come before the row of the desired index.
For this, we make use of the concept of combinations studied earlier to rewrite the numbers in the Pascal’s triangle. We know that  and is a non-negative integer .Also ,
and is a non-negative integer .Also , 
The Pascal’s triangle can now be rewritten as (Fig 8.3)

Observing this pattern, we can now write the row of the Pascal’s triangle for any index without writing the earlier rows. For Example, for the index 7 the row would be.
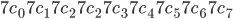
Thus, using this row and the observations (i), (ii) and (iii), we have

An expansion of a binomial to any positive integral index say n can now be visualised using these observations. We are now in a position to write the expansion of a binomial to any positive integral index.
- Binomial theorem for any positive integer n :

Observations:
- The notation
 stand for
stand for 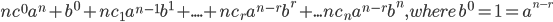
Hence the theorem can also be stated as
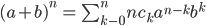
- The coefficients
 occuring in the binomial theorem are known as binomial coefficients.
occuring in the binomial theorem are known as binomial coefficients. - There are (n + 1) terms in the expansion of
 , i.e., one more than the index
, i.e., one more than the index - In the successive terms of the expansion the index of a goes on decreasing by unity. It is n in the first term, n –1) in the second term, and so on ending with zero in the last term. At the same time the index of b increases by unity , starting with zero in the first term, 1 in the second and so on ending with n in the last term
- In the expansion of
 , the sum of the indices of a and b is n + 0 = n in the first term, (n – 1) + 1 = n in the second term and so on 0 + n = n in the last term. Thus, it can be seen that the sum of the indices of a and b is n in very term of Thus, it can be seen that the sum of the indices of a and b is n in every term of the expansion.
, the sum of the indices of a and b is n + 0 = n in the first term, (n – 1) + 1 = n in the second term and so on 0 + n = n in the last term. Thus, it can be seen that the sum of the indices of a and b is n in very term of Thus, it can be seen that the sum of the indices of a and b is n in every term of the expansion. - Taking a = x and b = –y , we obtain
- Taking a = 1, b = x , we obtain
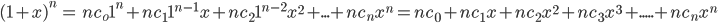
- Taking a = 1, b = – x, we obtain

NOTE : Some special cases: IN the expression of
"General-Terms" General and Middle Terms
- In the binomial expansion for
 we observe that the first term is
we observe that the first term is 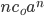 he second term is
he second term is 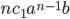 the third term is
the third term is , and so on. Looking at the pattern of the successive terms we can say that the
, and so on. Looking at the pattern of the successive terms we can say that the 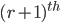 term is also called the general term of the expansion
term is also called the general term of the expansion  It is denoted by
It is denoted by 
- Regarding the middle term in the expansion
 , when be n + 1.since n is odd . Therefore the middle term is
, when be n + 1.since n is odd . Therefore the middle term is 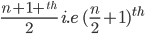 term
term
i) If n is odd, then n +1 is even, so there will be two middle terms in the expansion, namely,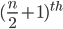 term and
term and  terms.
terms. - In the expansion of
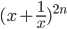 , where x ≠ 0, the middle term is
, where x ≠ 0, the middle term is  i.e.,
i.e.,
(n + 1)th term, as 2 n is even. It is given by (constant).
(constant).
This term is called the term independent of x or the constant term.
Point to be Remember:
- The expansion of a binomial for any positive integral n is given by Binomial

- The coefficients of the expansions are arranged in an array. This array is called Pascal’s triangle.
- The general term of an expansion

- In the expansion
 if n is even, then the middle term is the
if n is even, then the middle term is the
 terms.
terms.
Binomial Theorem Questions from previous year exams
Binomial theorem
Important Video - Binomial Theorem





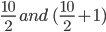





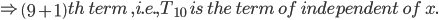
![T_{10}\: =\: ^{15}C_{9}\left ( x^{3} \right )^{15-9}\:\left [ \frac{2}{x^{2}} \right ]^{9}\: =\: ^{15}\: C_{6}.2^{9}.](https://questionpaper.org/wp-content/plugins/latex/cache/tex_524c8a440df50cbcb81ea46dd5d3a391.gif)






![\frac{(9+2x)^{\frac{1}{2}}(3+4x)}{\sqrt[5]{1-x}}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_a664a583f40ecd6d348a0d6b3a5fb7c8.gif)


![3\left [ 3+\frac{x}{3}+4x \right ]\left ( 1+\frac{x}{5} \right )](https://questionpaper.org/wp-content/plugins/latex/cache/tex_3c72ee9d74572a672de4f2ea31e0c1a8.gif)
![3\left [ 3+\frac{x}{3}+4x+\frac{3x}{5} \right ]\:=\:9+\frac{74x}{5}\: nearly](https://questionpaper.org/wp-content/plugins/latex/cache/tex_92ef0890a56f9eb6f2cf0d2713808fcb.gif)


![4^{\frac{-2}{5}}\left[\frac{\frac{-2}{5}(\frac{-2}{5}-1)(\frac{-2}{5}-2)....(\frac{-2}{5}-r+1)}{r!}\right]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_b8829c67a901046134e1df75b0bede96.gif)
![4^{\frac{-2}{5}}\left [\frac{ 2\times 7\times 12.....(5r-3)}{r!}\left ( \frac{7x}{20}^{r} \right ) \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_78cfb01d28c5a220d45f17363d0233c7.gif)


![(2-4x)(1-2x)^{2}\: =\:\left(2-4x\right)\times\left[1+2(2x)+3(2x)^{2}+n(2x) ^{n-1}+(n+1)(2x)^{a}+....\right]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_b0abf01f6c90c34453c1a95d35b180b2.gif)






![4\left [ 1+\frac{x^{2}}{8}+.... \right ]-3\left [ 1+\frac{2x^{2}}{9}+.... \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_c99476a21fb6c6f4f2b82e50012e24d0.gif)

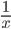

![2x\left [ 1+\frac{2}{x^{2}}-\left ( \frac{2}{x^{4}} \right )... \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_9b1f32ef194b91b045510043f837701d.gif)
![-2x\left [ 1+\frac{9}{8x^{2}}-\frac{81}{128x^{4}}+... \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_e466fb418dffc0639eeddf26b9ef159a.gif)





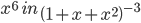



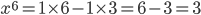
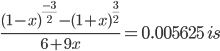

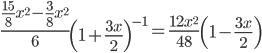



![\left ( \sqrt{2}+1 \right )^{6}+\left ( \sqrt{2}-1 \right )^{6}=\left [ ^{6}C_{0}\left ( \sqrt{2} \right )^{0}1^{6} +^{6}C_{1}(\sqrt{2})^{1}6^{1}+...^{6}C_{6}(\sqrt{2})^{6}1^{0}\right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_0fa29d1e13bc73dd054c5dfd3ff2dd2a.gif)
![+\left [ ^{6}C_{0}\left ( \sqrt{2} \right )^{0}1^{6}-^{6}C_{1}\left ( \sqrt{2} \right )^{1}6^{1}+^{6}C_{6}\left ( \sqrt{2} \right )^{6}1^{0} \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_556fb49f9f20946eb84794f6fe2db3ee.gif)
![2\left [ ^{6} C_{0}\left ( \sqrt{2} \right )^{0}1^{6}+^{6}C_{2}\left ( \sqrt{2} \right )^{2}1^{4}+...^{6}C_{6}\left ( \sqrt{2} \right )^{6}1^{0}\right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_38d1809a52695270b733d3cd08e3c516.gif)





0 Comments