Probability In an experiment if ‘ n ‘ is the number of exhaustive cases and ‘m’ is the number of favourable cases of an event A. Then the probability of event A is denoted by P(A).
P(A) = 
Probability Theory
- Random Experiment : An experiment in which all possible out comes are known and the exact output cannot be predicated in advance is called Random Experiment.
EXAMPLE :
(i) Tossing a fair coin
(ii) Rolling an unbiased dice
(iii) Drawing a card from a pack of well shuffled cards - Trail : Conducting a Random Experiment once is known as a Trail
- Outcome : The result of a Trail in the random experiment is called as Outcome
EXAMPLE : In tossing a single coin outcomes are H and T - Sample Space : A set of all possible outcomes of a random experiments is known as Sample Space
EXAMPLE :
( i ) In the experiment of tossing a coin the sample space S H,T
( ii ) If Two coins are tossed then S HH,HT,TH,TT
( iii ) In throwing a die S 1,2,3,4,5,6 - Event : Any non-empty subset of a Sample Space is called an Event
EXAMPLE :
( i ). in Tossing a single coin getting Head or Tail is an Event
( ii )Getting an Ace (or) Diamond from a pack of 52 cards is an event - Exhaustive Events : The total number of possible outcomes of an experiment is known as Exhaustive Events
EXAMPLE : In the experiment of throwing a die the total number of possible outcomes = 6 - Favourable Events : The number of event which favour the happing of the events are known as Favourable Cases (or) Events
EXAMPLE : In tossing two dice the number of cases favourable to getting the sum 3 is (2, 1), (1, 2) i.e., 2 - Mutually Exclusive Events : If two events have no common outcomes then they are called Mutually Exclusive
EXAMPLE: In tossing a coin the events Head & Tail are mutually exclusive because Head & Tail cannot happen at the same time. - Independent Events : Two events are said to be independent if the happening of one event does not affect the happening of the other.
- Dependent Events : Two events are said to be dependent if the happening of an event will affect the happening of the other event .
EXAMPLE: If we draw a card from a pack of 52 cards and replace it before we draw a second card. The second card is independent of first one. If we don’t replace the first card before the second draw. The second draw depends on the first one. - Axioms of Probability : Let S be the sample space and A be the event i.e.,
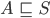
1.
2. P(S) = 1
3. If A and B are mutually exclusive ( Disjoint i.e., )
)
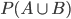 = P(A)+P(B)
= P(A)+P(B) - Results of Probability :
1. for any two events A & B ,
2. If denotes compliment of event A then ,
denotes compliment of event A then ,  = 1-P(A)
= 1-P(A)
3. For any two events A & B ,
4. For any three events A, B & C ,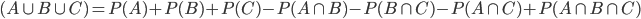
Probability Examples and Probability Solutions
Question 1: A die is rolled, find the probability that an even number is obtained.
Solution : Let us first write the sample space S of the experiment.
S = {1,2,3,4,5,6}
Let E be the event "an even number is obtained" and write it down.
E = {2,4,6}
We now use the formula of the classical probability.
P(E) = 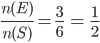
Question 2: Two coins are tossed, find the probability that two heads are obtained.
Note: Each coin has two possible outcomes H (heads) and T (Tails).
Solution: The sample space S is given by.
S = {(H,T),(H,H),(T,H),(T,T)}
Let E be the event "two heads are obtained".
E = {(H,H)}
We use the formula of the classical probability.
P(E) = 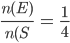
Question 3: You toss a coin AND roll a die. What is the probability of getting a tail and a on the die?
Solution 3: Probability of getting a tail when a single coin is tossed = 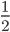
Probability of getting 4 when a die is thrown = 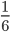
Required probability =
Question 4: A number is selected from the numbers 1, 2, 3 and then a second number y is randomly selected from the numbers 1, 4, 9. What is the probability that the product xy of the two numbers will be less than 9 ways
Solution 4: Number X can be selected in three ways and corresponding to each such way there are three ways of selecting number y.
Therefore, two numbers can be selected in 9 ways.
The favourable number of elementary events for which the product xy of the two numbers will less than 9 = (1,1),(1,4),(2,1),(2,4),(3,1) = 5
Hence the required probability =
Question 5: Find the probability of having 53 Sundays in
( i ) a leap year (ii) a non leap year
Solution 5: An ordinary year has 365 days i.e., 52 weeks and 1 odd day.
This day can be any one of the 7 days of the week,
 P(that this day is Sunday) =
P(that this day is Sunday) = 
Hence,  P(an Ordinary Year has 53 Sundays) =
P(an Ordinary Year has 53 Sundays) = 
A leap year has 366 days. i.e., 52 weeks and 2 odd days
This day can be any one of the 7 days of the week
 P(that this day is Sunday) =
P(that this day is Sunday) = 
Hence  P(a leap Year has 53 Sundays) =
P(a leap Year has 53 Sundays) = 
Question 6: Two cards are drawn at random from a pack of 52 cards. What is the probability that either both are black and both are queen.
Solution 6: Let S be the Sample space. Then
n(S) = Number of ways of drawing 2 balls out of (6+4) = 
Let E = Event of getting both balls of the same colour . Then
N(E) = Number of ways of drawing ( 2 balls out 6 )or ( 2 balls out of 4)
=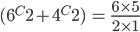
P(E) = 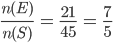
Probability Questions from Previous Year Exams
Probability Aptitude
Probability Video lectures




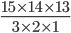
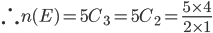

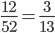



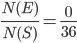








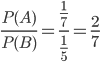


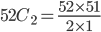


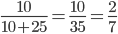


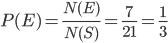
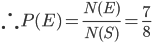
0 Comments