Trigonometry’ is derived from the Greek words ‘trigon’ and ‘metron’ and it means ‘measuring the sides of a triangle’. The subject was originally developed to solve geometric problems involving triangles. It was studied by sea captains for navigation, surveyor to map out the new lands, by engineers and others. Currently, trigonometry is used in many areas such as the science of seismology, designing electric circuits, describing the state of an atom, predicting the heights of tides in the ocean, analysing a musical tone and in many other areas. In earlier classes, we have studied the trigonometric ratios of acute angles as the ratio of the sides of a right angled triangle. We have also studied the trigonometric identities and application of trigonometric ratios in solving the problems related to heights and distances. In this Chapter, we will generalist the concept of trigonometric ratios to trigonometric function and study their properties.
Trigonometric Angles
Angle is a measure of rotation of a given ray about its initial point. The original ray is
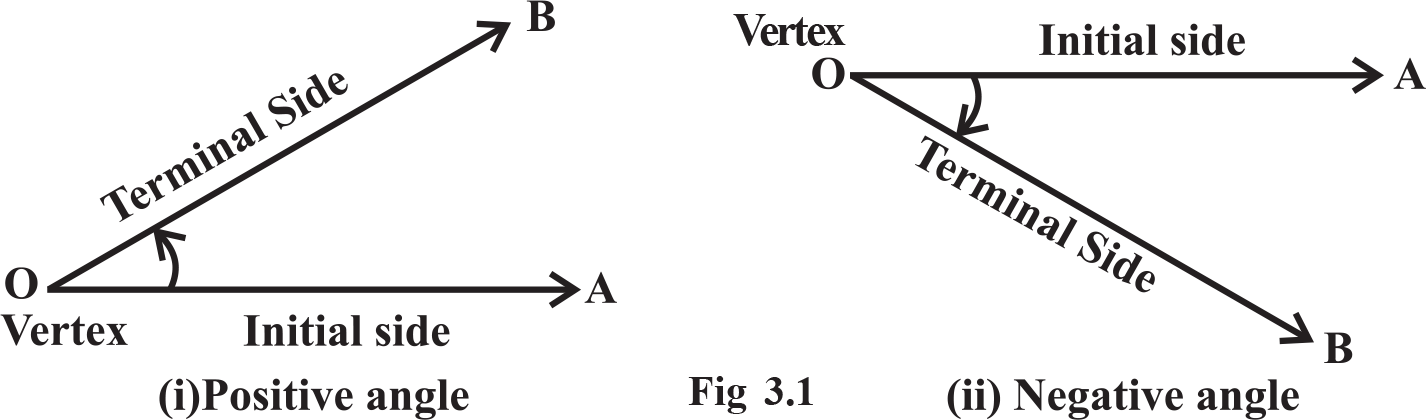
called the initial side and the final position of the ray after rotation is called the terminal side of the angle. The point of rotation is called the vertex. If the direction of rotation is anticlockwise, the angle is said to be positive and if the direction of rotation is clockwise, then the angle is negative (Fig 3.1)
The measure of an angle is the amount of rotation performed to get the terminal side from the initial side. There are several units for measuring angles. The definition of an angle suggests a unit, viz. one complete revolution from the position of the initial side as indicated in (Fig 3.2)
 This is often convenient for large angles. For example, we can say that a rapidly spinning wheel is making an angle of say 15 revolution per second. We shall describe two other units of measurement of an angle which are most commonly used, viz. degree measure and radian measure.
This is often convenient for large angles. For example, we can say that a rapidly spinning wheel is making an angle of say 15 revolution per second. We shall describe two other units of measurement of an angle which are most commonly used, viz. degree measure and radian measure.
Degree Measure: If a rotation from the initial side to terminal side is  of a revolution, the angle is said to have a measure of one degree, written as 1°. A degree is divided into 60 minutes, and a minute is divided into 60 seconds . One sixtieth of a degree is called a minute, written as 1′, and one sixtieth of a minute is called a second, written as 1″.
of a revolution, the angle is said to have a measure of one degree, written as 1°. A degree is divided into 60 minutes, and a minute is divided into 60 seconds . One sixtieth of a degree is called a minute, written as 1′, and one sixtieth of a minute is called a second, written as 1″.
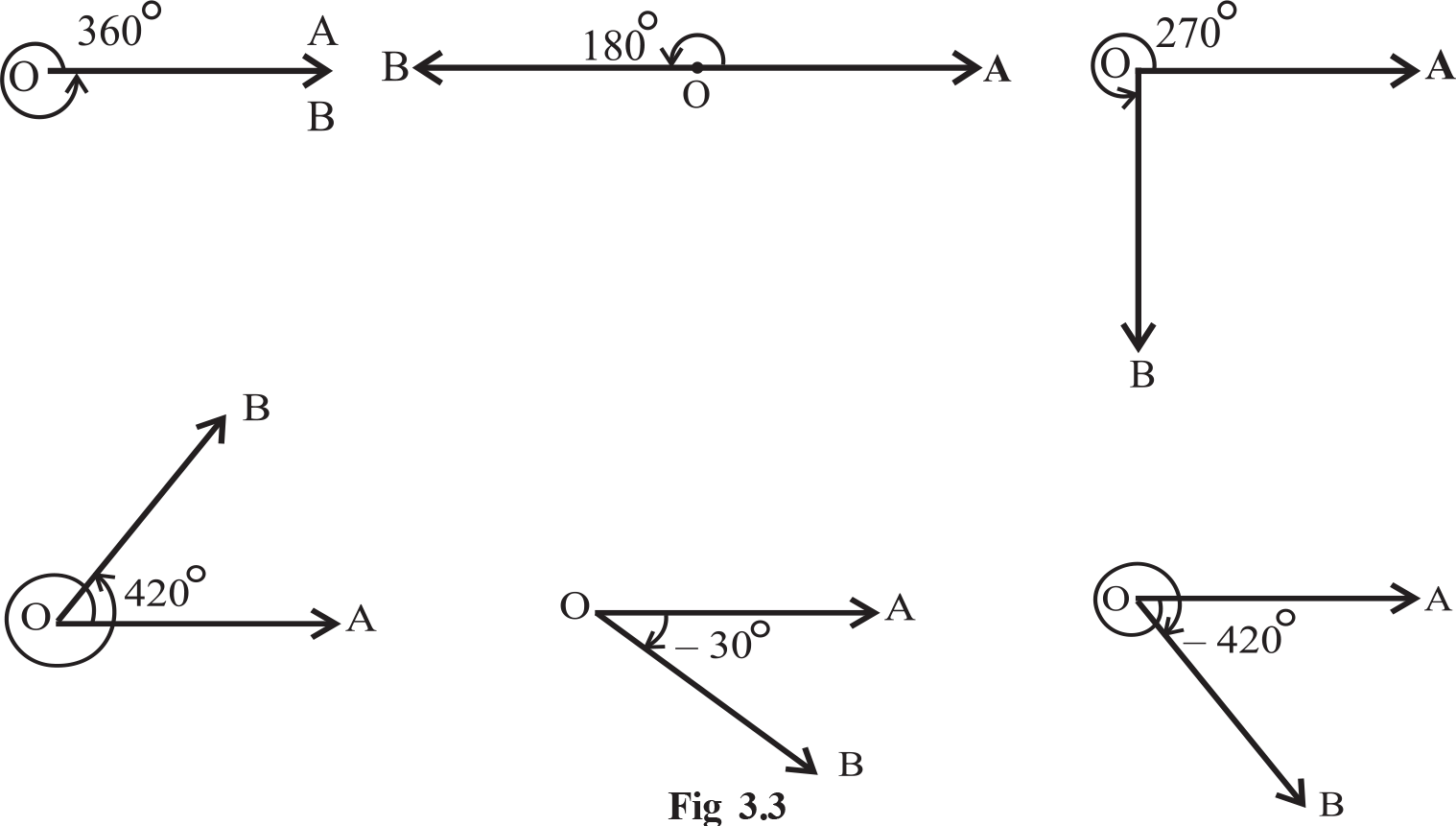
Thus, 1° = 60′, 1′ = 60″ Some of the angles whose measures are 360°,180°, 270°, 420°, – 30°, – 420° are shown in (Fig 3.3)
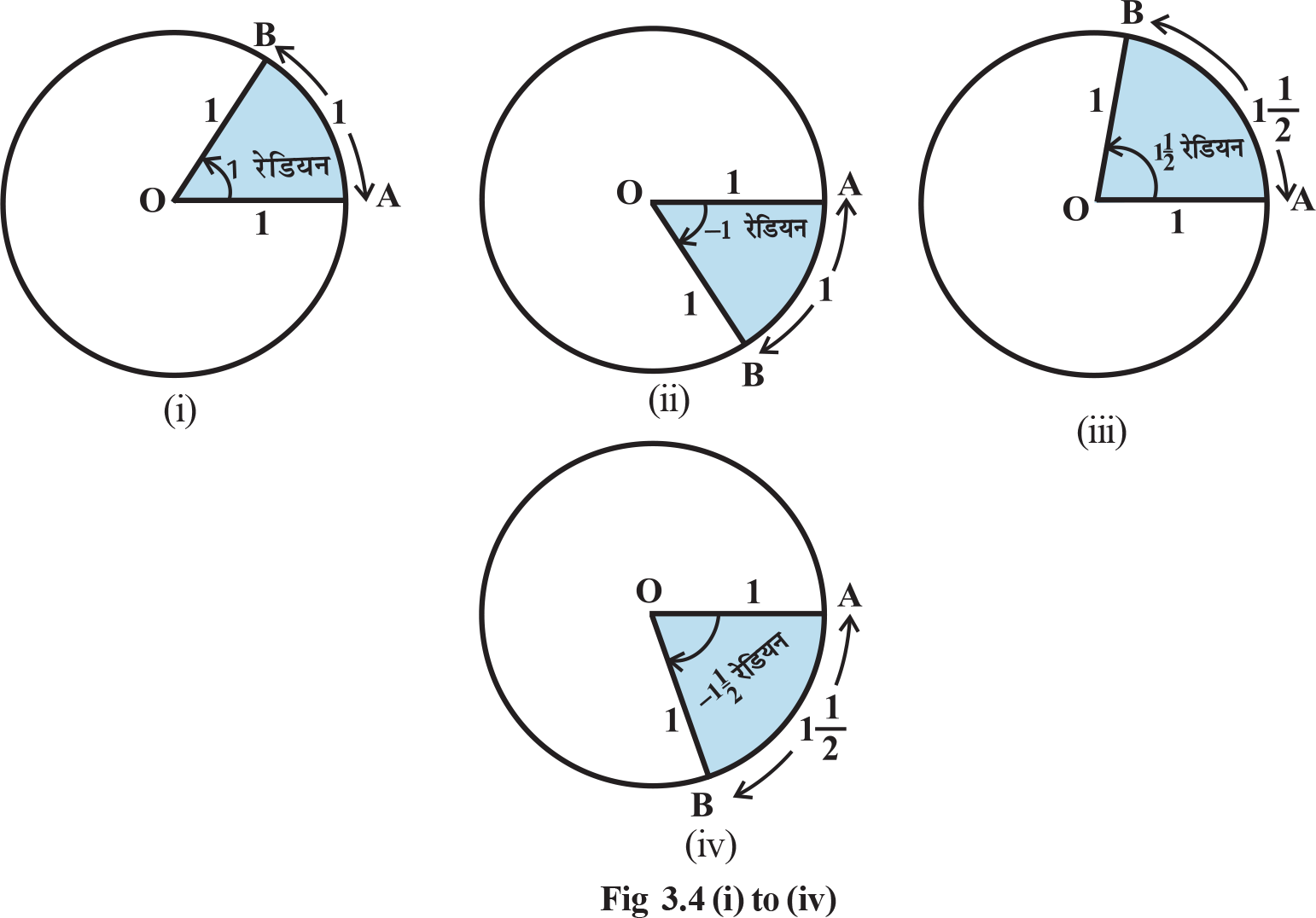
Radian Measure: There is another unit for measurement of an angle, called the radian measure. Angle subtended at the centre by an arc of length 1 unit in a unit circle (circle of radius 1 unit) is said to have a measure of 1 radian. In the Fig 3.4(i) to (iv), OA is the initial side and OB is the terminal side. The figures show the angles whose measures are 1 radian, –1 radian  radian and
radian and 
We know that the circumference of a circle of radius 1 unit is 2π. Thus, one complete revolution of the initial side subtends an angle of 2π radian. More generally, in a circle of radius r, an arc of length r will subtend an angle of 1 radian. It is well-known that equal arcs of a circle subtend equal angle at the centre. Since in a circle of radius r, an arc of length r subtends an angle whose measure is 1 radian, an arc of length l will subtend an angle whose measure is  radian. Thus, if in a circle of radius r, an arc of length l subtends an angle θ radian at the centre, we have
radian. Thus, if in a circle of radius r, an arc of length l subtends an angle θ radian at the centre, we have
 or l = r
or l = r
Relation Between Radian and Real Numbers

Consider the unit circle with centre O. Let A be any point on the circle. Consider OA as initial side of an angle. Then the length of an arc of the circle will give the radian measure of the angle which the arc will subtend at the centre of the circle. Consider the line PAQ which is tangent to the circle at A. Let the point A represent the real number zero, AP represents positive real number and AQ represents negative real numbers (Fig 3.5). If we rope the line AP in the anticlockwise direction along the circle, and AQ in the clockwise direction, then every real number will correspond to a radian measure and conversely. Thus, radian measures and real numbers can be considered as one and the same.
Relation between Degree and Radian:
Since a circle subtends at the centre an angle whose radian measure is 2π and its degree measure is 360°, it follows that 2π radian = 360° or π radian = 180° The above relation enables us to express a radian measure in terms of degree measure and a degree measure in terms of radian measure. Using approximate value of π as  , we have
, we have
1 radian = 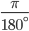 = 0.01746 radian approximately. The relation between degree measures and radian measure of some common angles are given in the following table:
= 0.01746 radian approximately. The relation between degree measures and radian measure of some common angles are given in the following table:

Example : 1 Convert 40° 20′ into radian measure.
Solution : We know that 180° = π radian.
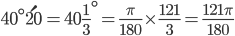 radian
radian
Trigonometric Functions
In earlier classes, we have studied trigonometric ratios for acute angles as the ratio of sides of a right angled triangle. We will now extend the definition of trigonometric ratios to any angle in terms of radian measure and study them as trigonometric functions. Consider a unit circle with centre at origin of the coordinate axes. Let P (a, b) be any point on the circle with angle AOP = x radian, i.e., length of arc AP = X IN (3.6)
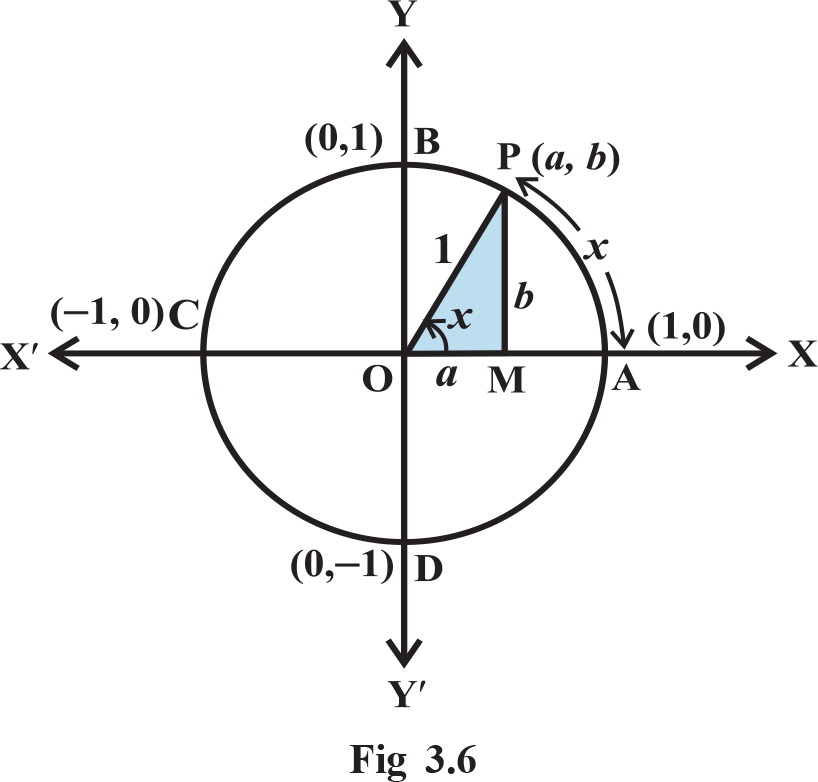
We define cos x = a and sin x = b Since ΔOMP is a right triangle, we have 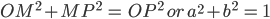 Thus, for every point on the unit circle we have
Thus, for every point on the unit circle we have  Since one complete revolution subtends an angle of 2π radian at the centre of the circle, ∠AOB =
Since one complete revolution subtends an angle of 2π radian at the centre of the circle, ∠AOB = 
∠AOC = π and ∠AOD =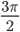 . All angles which are integral multiples of
. All angles which are integral multiples of  are called quadrantal angles. The coordinates of the points A, B, C and D are, respectively, (1, 0), (0, 1), (–1, 0) and (0, –1). Therefore, for quadrantal angles, we have.
are called quadrantal angles. The coordinates of the points A, B, C and D are, respectively, (1, 0), (0, 1), (–1, 0) and (0, –1). Therefore, for quadrantal angles, we have.
| cos 0° = 1 | sin 0° = 0, |
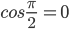 |
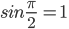 |
| cosπ = − 1 | sinπ = 0 |
 |
 |
| cos 2π = 1 | sin 2π = 0 |
Note:
1. sin x = 0 implies x = nπ, where n is any integer
2. cos x = 0 implies x =, where n is any integer.
We now define other trigonometric functions in terms of sine and cosine functions:
 , x ≠ nπ, where n is any integer.
, x ≠ nπ, where n is any integer. , , x ≠ =
, , x ≠ =  , where n is any integer.
, where n is any integer.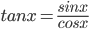 , x ≠ =
, x ≠ =  , where n is any integer
, where n is any integer , x ≠ n π, where n is any integer.
, x ≠ n π, where n is any integer.
We have shown that for all real x, 
It follows that ,
In earlier classes, we have discussed the values of trigonometric ratios for 0°, 30°, 45°, 60° and 90°. The values of trigonometric functions for these angles are same as that of trigonometric ratios studied in earlier classes. Thus, we have the following Table

The values of cosec x, sec x and cot x are the reciprocal of the values of sin x, cos x and tan x, respectively.
Sign of Trigonometric Functions: Let P (a, b) be a point on the unit circle with centre at the origin such that ∠AOP = x. If ∠AOQ = – x, then the coordinates of the point Q will be (a, –b)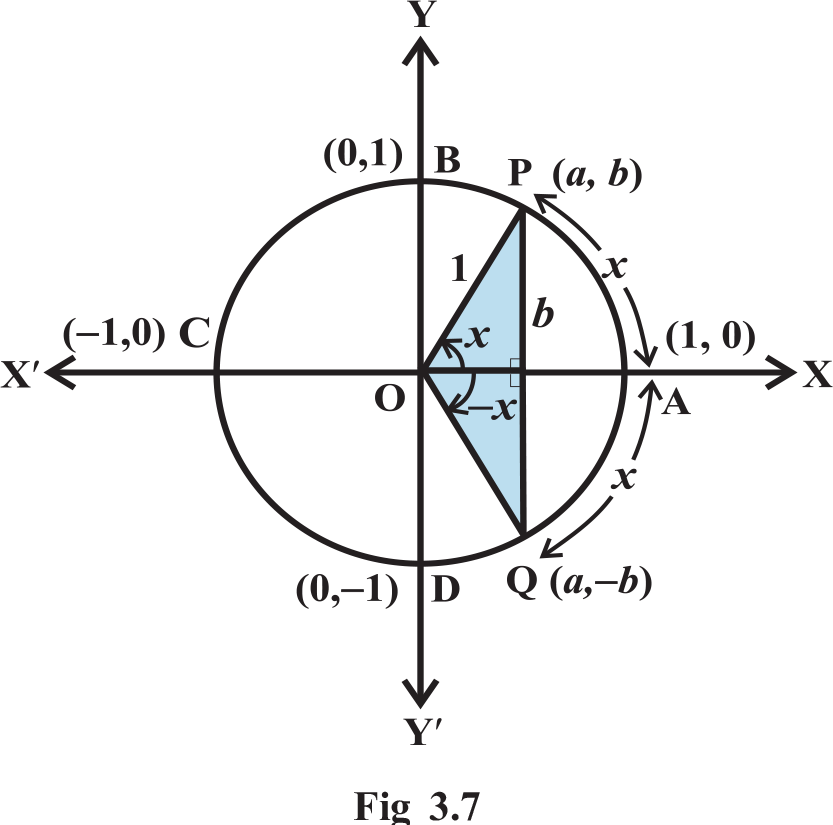 (Fig 3.7). Therefore
(Fig 3.7). Therefore
cos (– x) = cos x and sin (– x) = – sin x Since for every point P (a, b) on the unit circle, – 1 ≤ a ≤ 1 and
– 1 ≤ b ≤ 1, we have – 1 ≤ cos x ≤ 1 and –1 ≤ sin x ≤ 1 for all x. We have learnt in previous classes that in the first quadrant 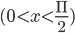 a and b are both positive, in the second quadrant
a and b are both positive, in the second quadrant  a is negative and b is positive, in the third quadrant
a is negative and b is positive, in the third quadrant
We can find the signs of other trigonometric functions in different quadrants. In fact, we have the following table.

Domain and Range of Trigonometric Functions: From the definition of sine and cosine functions, we observe that they are defined for all real numbers. Further, we observe that for each real number x,
– 1 ≤ sin x ≤ 1 and – 1 ≤ cos x ≤ 1 Thus, domain of y = sin x and y = cos x is the set of all real numbers and range is the interval [–1, 1], i.e., – 1 ≤ y ≤ Since cosec x = 1 sin x , the domain of y = cosec x is the set { x : x ∈ R and x ≠ n π, n ∈ Z} and range is the set {y : y ∈ R, y ≥ 1 or y ≤ – 1}. Similarly, the domain of y = sec x is the set {x : x ∈ R and x ≠ (2n + 1) π\2 , n ∈ Z} and range is the set {y : y ∈ R, y ≤ – 1or y ≥ 1}. The domain of y = tan x is the set {x : x ∈ R and x ≠ (2n + 1) /2 , n ∈ Z} and range is the set of all real numbers. The domain of y = cot x is the set {x : x ∈ R and x ≠ n π, n ∈ Z} and the range is the set of all real numbers.

Trigonometric Functions of Sum and Difference of Two Angles In this Section, we shall derive expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions. The basic results in this connection are called trigonometric identities. We have seen that
- sin (– x) = – sin x
- cos (– x) = cos x
- cos (x + y) = cos x cos y – sin x sin y
- cos (x – y) = cos x cos y + sin x sin y
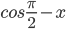 = sinx
= sinx = cosx
= cosx- sin (x + y) = sin x cos y + cos x sin y
- sin (x – y) = sin x cos y – cos x sin y
 = -sinx
= -sinx = cosx
= cosx- cos (π – x) = – cos x s
- sin (π – x) = sin x
- cos (π + x) = – cos x
- sin (π + x) = – sin x
- cos (2π – x) = cos x
- sin (2π – x) = – sin x
Trigonometric Important Formula


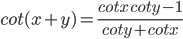
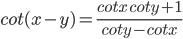
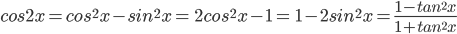
- sin 2x = 2 sinx cos x ==
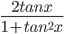
- tan2x = ==

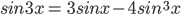
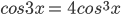 -3cosx
-3cosx

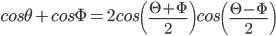
- 2 cos x cos y = cos (x + y) + cos (x – y)
- –2 sin x sin y = cos (x + y) – cos (x – y)
- 2 sin x cos y = sin (x + y) + sin (x – y)
- 2 cos x sin y = sin (x + y) – sin (x – y).
Trigonometric Point to be Remember
If in a circle of radius r, an arc of length l subtends an angle of θ radians, then
- l = r θ
- Radian measure = π/180 Degree measure* Degree measure
- Degree measure = 180/π *Radian measure

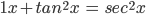
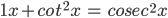
- cos (2nπ + x) = cos x
- sin (2nπ + x) = sin x
- sin (– x) = – sin x
- cos (– x) = cos x
Trigonometric Questions from Previous Year Exams
Trigonometry
Trigonometric Video Lectures




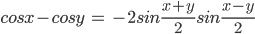
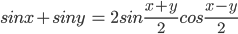
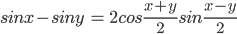
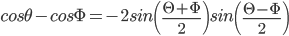

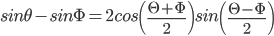
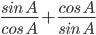

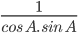
![\left [ sin^{2}\:A+cos^{2}\:A\:=\:1 \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_b15fda56a0f573279bc1149873aad790.gif)
![sec^{2}\theta\:cosec^{2}\theta -\left [ tan^{2}\theta +cot^{2}\theta \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_4c36e7a7a8138ef1f381ffd30363bc28.gif)
![\left ( 1+tan^{2}\theta \right )\left ( 1+cot^{2}\theta \right )-\left [ tan^{2}\theta +cot^{2} \theta \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_edc93749297fe7af6912691f873cee55.gif)






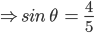

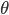
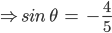



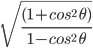


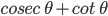

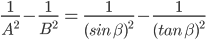
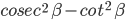


![\left [ Since\:sin^{2}\:\theta +cos^{2}\theta \:=\:1 \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_56051e3b1acf4cf09f0319ba4f20279a.gif)

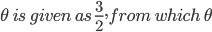

![\left [ sec\:\theta +(tan\:\theta -1) \right ]\left [ sec\:\theta -(tan\:\theta -1) \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_ae24bf68e19755461c7bfaf3210979d5.gif)


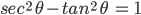


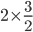




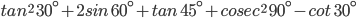


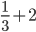
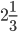


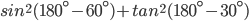


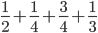




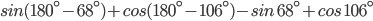
![sin\:68^{\circ}+\left [ -cos\:106^{\circ} \right ]-sin\:68^{\circ}+cos\:106^{\circ}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_f6f44e6296790e59314f4a7ba5845400.gif)
![\left [ Since,cos(180-\theta ) \right ]\:=\:-\:cos\:\theta](https://questionpaper.org/wp-content/plugins/latex/cache/tex_7774707681d9dac6a0d9dc5497c6b5bf.gif)


![\frac{\sqrt{3}}{2}+1+\left [ -cos\:60^{\circ} \right ]-sin\:30^{\circ}+\left [ -tan\:45^{\circ} \right ]+cos\:30^{\circ}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_fea400aec885162fce04f1dde3646677.gif)
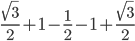


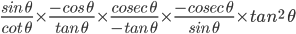


![sin(360^{\circ}+60^{\circ})\:cos\:(360^{\circ}+30^{\circ})+cos\left [ -360^{\circ}+60^{\circ} \right ]sin\left [ -360^{\circ}+30^{\circ} \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_1172137d21accce72ce33c2ce2d2cca0.gif)
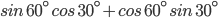

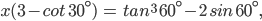

![\Rightarrow x\left [ 3-\sqrt{3} \right ]\:=\:(\sqrt{3})^{3}-2\times \frac{\sqrt{3}}{2}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_5a43f97b52764567ad382e86c1486bd8.gif)
![\Rightarrow x\times \sqrt{3}\:[\sqrt{3}-1]\:=\:3\sqrt{3}-\sqrt{3}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_c7d8a69957e4b33aac1f5ec5d9250349.gif)

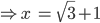
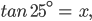
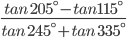
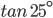
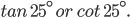
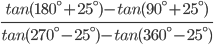
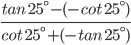

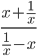
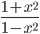





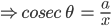




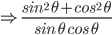
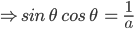
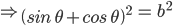

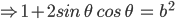
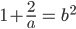


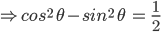


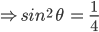
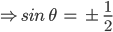
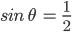


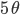
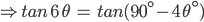
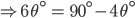

![sin\:5\: \theta ^{\circ}\: =\: sin\:45^{\circ}\: \: \left [ Since\:\theta \: =\: 9^{\circ} \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_a71e73d687d470bef2f003e00430af2f.gif)
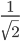
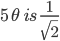
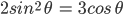

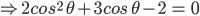
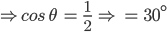

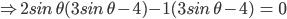
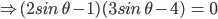
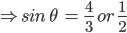
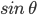








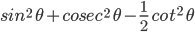

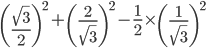



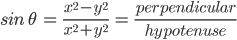
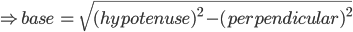



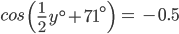



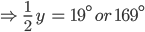
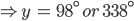

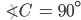

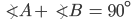
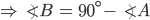
![sin\:90^{\circ}\left [ sec\: A.\: cosec(90^{\circ}-A)-tan\:A.\:cot\:(90^{\circ}-A)\right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_0e63e8e265a3d816772276de7eccb197.gif)
0 Comments