Consider the two sets P = {a,b,c} and Q = {Ali, Bhanu, Binoy, Chandra, Divya}.
The cartesian product of P and Q has 15 ordered pairs which can be listed as P × Q = {(a, Ali),(a,Bhanu), (a, Binoy), ...,
(c, Divya)}. We can now obtain a subset of P × Q by introducing a relation R between the first element x and the
second element y of each ordered pair ( x , y) as R= { (x,y) : x is the first letter of the name  .Then R = {(a, Ali), (b, Bhanu), (b, Binoy), (c, Chandra)}A visual representation of this relation R (called an arrow diagram) is shown in Fig 2.4
.Then R = {(a, Ali), (b, Bhanu), (b, Binoy), (c, Chandra)}A visual representation of this relation R (called an arrow diagram) is shown in Fig 2.4
Definition: A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product A×B. The subset is derived by describing a relationship between the first element and the second element of the ordered pairs in A×B. The second element is called the image of the first element. or
The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain
of the relation R.. or
Definition: The set of all second elements in a relation R from a set A to a set B is called the range of the relation R. The whole set B is called the codomain of the relation R. Note that range ⊆ co-domain.
Note:
- A relation may be represented algebraically either by the Roster method or by the Set-builder method.
- An arrow diagram is a visual representation of a relation.
Important Point: The total number of relations can be define from a set A to a set B is the number of possible subset of a A*B. If n(A) = P and n (B) = q , then n(A*B) = pq and the total number of relation is 2pq
Relations and Functions Examples
Example: Let A = {1,2,3,4,5,6}.Define a relation R from A to A by R = {(x,y): y = x+1}
- Depict the relation using an arrow diagram.
- Write down the domain , codomain and range of R
Solution:
- By the definition of the relation R{(1,2),(2,3),(3,4),(4,5),(5,6)}.
The corresponding arrow diagram is shown in Fig 2.5. - We can see that the
domain ={1, 2, 3, 4, 5,} Similarly, the range = {2, 3, 4, 5, 6} and the codomain = {1, 2, 3, 4, 5, 6}
Functions
In this Section, we study a special type of relation called function. It is one of the most important concepts in mathematics. We can, visualise a function as a rule, which produces new elements out of some given elements. There are many terms such as ‘map’ or ‘mapping’ used to denote a function.
Definition: A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B. In other words, a function f is a relation from a non-empty set A to a non- empty set B such that the domain of f is A and no two distinct ordered pairs in f have the same first element.
If f is a function from A to B and (a, b) ∈ f, then f (a) = b, where b is called the image of a under f and a is called the preimage of b under f. The function f from A to B is denoted by f: A B.
Points to be Remember
- Ordered pair A pair of elements grouped together in a particular order .
- Cartesian product A × B of two sets A and B is given by A × B = {(a,b): a∈A, b ∈ B} in In particular
R× R= {(x,y): x,y ∈R}and R× R× R= (x, y, z): x, y, z∈ R} and R× R× R= (x, y, z): x, y, z∈ R}- If (a, b) = (x, y), then a = x and b = y .
- If n(A) = p and n(B) = q , then n (A × B) = pq
- A × φ = φ
- In general, A × B ≠ B × A.
- Relation A relation R from a set A to a set B is a subset of the Cartesian product A × B obtained by describing a relationship between the first element x and the second element y of the ordered pairs in A × B.
- The image of an element x under a relation R is given by y, where (x, y) ∈ R,
- The domain of R is the set of all first elements of the ordered pairs in a relation R.
- The range of the relation R is the set of all second elements of the ordered pairs in a relation R.
- Function: A function f from a set A to a set B is a specific type of relation for which every element x of set A has one d 0nly one image y in set B. write f: A→B, where f(x) = y.
- A is the domain and B is the co domain of f.
(f +g) (x) = f (x) +g(x), x ∈X
(f –g) (x) = f (x) – g(x), x ∈X
(f.g) (x) = f (x) .g (x), x ∈X
(kf) (x) =kf (x) ), x ∈ X, where kis a real number.
Relations and Functions Questions from Previous Year Exams
Relation and function
Relations and Functions Video Lecture






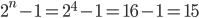


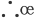
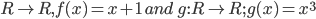



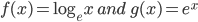

![\log_{e}e^{x}=x\log_{e}e=x\: \left [\because \log_{e}e=1 \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_eda6a5f727a64801d6e98d24cb45f08b.gif)
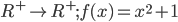


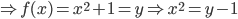
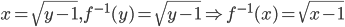




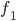




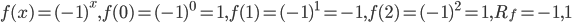


![D_{f}=\left [ 4,\infty \right]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_34adeda029f5eb9a4804b6271ad90b5f.gif)




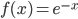

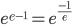
0 Comments