In mensuration we shall study about some other curves, viz., circles, ellipses, parabolas and hyperbolas. The names parabola and hyperbola are given by Apollonius. These curves are in fact, known as conic sections or more commonly conics because they can be obtained as intersections of a plane with a double napped right circular cone. These curves have a very wide range of  applications in fields such as planetary motion, design of telescopes and antennas, reflectors in flashlights and automobile headlights, etc. Now, in the subsequent sections we will see how the intersection of a plane with a double napped right circular cone results in different types of curves.
applications in fields such as planetary motion, design of telescopes and antennas, reflectors in flashlights and automobile headlights, etc. Now, in the subsequent sections we will see how the intersection of a plane with a double napped right circular cone results in different types of curves.
Sections of a Cone
Let l be a fixed vertical line and m be another line intersecting it at a fixed point V and inclined to it at an angle α (Fig 11.1). Suppose we rotate the line m around the line l in such a way that the angle α remains constant. Then the surface generated is a double-napped right circular hollow cone herein after referred as cone and extending indefinitely far in both directions (Fig.11.2)

The point V is called the vertex; the line l is the axis of the cone. The rotating line m is called a generator of the cone. The vertex separates the cone into two parts called nappes. If we take the intersection of a plane with a cone, the section so obtained is called a conic section. Thus, conic sections are the curves obtained by intersecting a right circular cone by a plane.
We obtain different kinds of conic sections depending on the position of the intersecting plane with respect to the cone and by the angle made by it with the vertical axis of the cone. Let β be the angle made by the intersecting plane with the vertical axis of the cone (Fig11.3). The intersection of the plane with the cone can take place either at the vertex of the cone or at any other part of the nappe either below or above the vertex.
Introduction to Conic Sections
Circle, Ellipse, Parabola and Hyperbola
When the plane cuts the nappe (other than the vertex) of the cone, we have the following situations:
(a) When β = 90o , the section is a circle (Fig 11.4)
(b) When α < β < 90o , the section is an ellipse (Fig 11.5)
(c) When β = α; the section is a parabola (Fig 11.6)
(In each of the above three situations, the plane cuts entirely across one nappe of the cone).
(d) When 0 ≤ β < α; the plane cuts through both the nappes and the curves of intersection is a hyperbola (Fig11.7)

Conic Sections: Intro to Circles
Conic Sections: Intro to Ellipses
Conic Sections: Intro to Hyperbolas
Degenerated conic sections
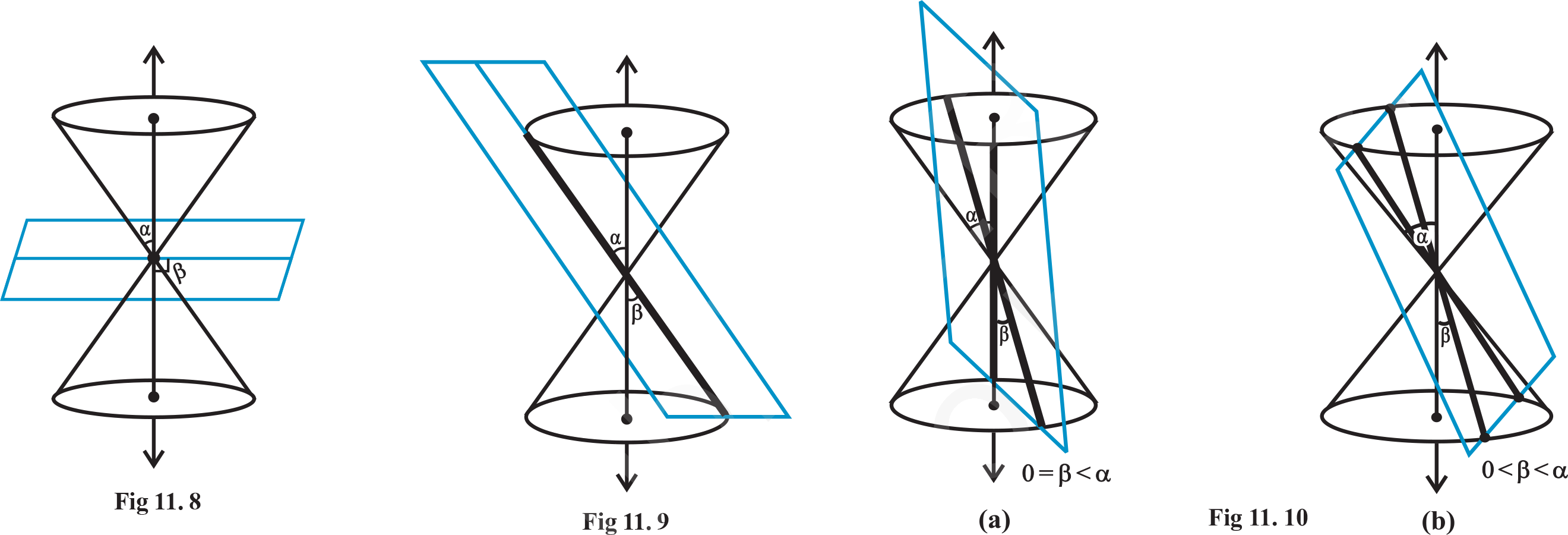
When the plane cuts at the vertex of the cone, we have the following different cases:
(a) When α < β ≤ 90o , then the section is a point (Fig 11.8)
(b) When β = α, the plane contains a generator of the cone and the section is a straight line (Fig 11.9)
It is the degenerated case of a parabola.
(c) When 0 ≤ β < α, the section is a pair of intersecting straight lines (Fig 11.10) It is the degenerated case of a hyperbola.
In the following sections, we shall obtain the equations of each of these conic sections in standard form by defining them based on geometric properties.
Circle 1: A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
The fixed point is called the centre of the circle and the distance from the centre to a point on the circle is called the radius of the circle (Fig 11.11)

The equation of the circle is simplest if the centre of the circle is at the origin. However, we derive below the equation of the circle with a given centre and radius (Fig 11.12)
Given C (h, k) be the centre and r the radius of circle. Let P(x, y) be any point on the circle .Then, by the definition, | CP | = r . By the distance formula, we have
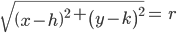
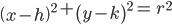
This is the required equation of the circle with centre at (h,k) and radius r .
Example: Find the equation of the circle with centre (–3, 2) and radius 4.
Solution: Here h = –3, k = 2 and r = 4. Therefore, the equation of the required circle is

= 
Example 2: Find the centre and the radius of the circle
Solution: The given equation is
Now, completing the squares within the parenthesis, we get
= $
$
=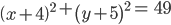
=
therefore, the given circle has centre at (– 4, –5) and radius 7
Parabola
2 A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line) in the plane. The fixed line is called the directrix of the parabola and the fixed point F is called the focus (Fig 11.13) ‘Para’ means ‘for’ and ‘bola’ means ‘throwing’, i.e., the shape described when you throw a ball in the air).
Note: If the fixed point lies on the fixed line, then the set of points in the plane, which are equidistant from the fixed point and the fixed line is the straight line through the fixed point and perpendicular to the fixed line. We call this straight line as degenerate case of the parabola.
A line through the focus and perpendicular to the directrix is called the axis of the parabola. The point of intersection of parabola with the axis is called the vertex of the parabola (Fig 11.14)
Standard Equations of Parabola: The equation of a parabola is simplest if the vertex is at the origin and the axis of symmetry is along the x-axis or y-axis. The four possible such orientations of parabola are shown below in (Fig 11.15)

where PB is perpendicular to l. The coordinates of B are (– a, y). By the distance formula, we have
 and
and 
since PF = PB we get ,

 or
or 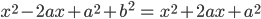
or  (a > 0)
(a > 0)
Hence, any point on the parabola satisfies or 
Note: The standard equations of parabolas have focus on one of the coordinate axis; vertex at the origin and thereby the directrix is parallel to the other coordinate axis. However, the study of the equations of parabolas with focus at any point and any line as directrix is beyond the scope here.
From the standard equations of the parabolas, we have the following observations:
1. Parabola is symmetric with respect to the axis of the parabola.If the equation has a  term, then the axis of symmetry is along the x-axis and if the equation has an
term, then the axis of symmetry is along the x-axis and if the equation has an  term, then the axis of symmetry is along the y-axis.
term, then the axis of symmetry is along the y-axis.
2. When the axis of symmetry is along the x-axis the parabola opens to the
(a) right if the coefficient of x is positive,
(b) left if the coefficient of x is negative.
3. When the axis of symmetry is along the y-axis the parabola opens
(c) upwards if the coefficient of y is positive.
(d) downwards if the coefficient of y is negative.
Latus Rectum
Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose end points lie on the parabola (Fig 11.17)
To find the Length of the latus rectum of the parabola  = 4ax (Fig 11.18)
= 4ax (Fig 11.18)
By the definition of the parabola, AF = AC.
But AC = FM = 2a
Hence AF = 2a.
And since the parabola is symmetric with respect to x-axis AF = FB and so AB = Length of the latus rectum = 4a.

Example: Find the coordinates of the focus, axis, the equation of the directrix and latus rectum of
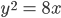
Solution: The given equation involves  , so the axis of symmetry is along the x-axis.
, so the axis of symmetry is along the x-axis.
The coefficient of x is positive so the parabola opens to the right. Comparing with the given equation  , we find that a = 2.
, we find that a = 2.
Thus, the focus of the parabola is (2, 0) and the equation of the directrix of the parabola is x = – 2 (Fig 11.19)
Length of the latus rectum is 4a = 4 × 2 = 8.
Ellipse
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant. The two fixed points are called the foci (plural of ‘focus’) of the ellipse (Fig 11.10)
Note : The constant which is the sum of the distances of a point on the ellipse from the two fixed points is always greater than the distance between the two fixed points.
The mid point of the line segment joining the foci is called the centre of the ellipse. The line segment through the foci of the ellipse is called the major axis and the line segment through the centre and perpendicular to the major axis is called the minor axis. The end points of the major axis are called the vertices of the ellipse.(Fig 11.21)

We denote the length of the major axis by 2a, the length of the minor axis by 2b and the distance between the foci by 2c. Thus, the length of the semi major axis is a and semi-minor axis is b
Relationship between semi-major axis, semi-minor axis and the distance of the focus from the centre of the ellipse
Relationship between semi-major axis, semi-minor axis and the distance of the focus from the centre of the ellipse (Fig 11.23). [/su_heading]
Take a point P at one end of the major axis. Sum of the distances of the point P to the foci is
F1 P + F2 P = F1 O + OP + F2 P (Since, F1 P = F1 O + OP) = c + a + a – c = 2a 
Take a point Q at one end of the minor axis. Sum of the distances from the point Q to the foci is ![2F_{1}Q\:\:F_{2}Q=\sqrt{a^{2}+c^{2}}+\sqrt{b^{2}+c^{2}}=\sqrt[2]{b^{2}+a^{2}}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_4740bd46ec7f21072157792dd5367a7b.gif)
Since both P and Q lies on the ellipse. By the definition of ellipse, we get,
![\sqrt[2]{b^{2}+c^{2}}=2a](https://questionpaper.org/wp-content/plugins/latex/cache/tex_51d7f2bbb23043ad32c342d72d52294e.gif) i.e
i.e![\sqrt[a]{b^{2}+c^{2}}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_4c1df30d2fdf7b9ffc8c1f88640dc254.gif)
 i.e
i.e
Special Cases of an Ellipse In the equation 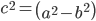 obtained above, if we keep a fixed and vary c from 0 to a, the resulting ellipses will vary in shape.
obtained above, if we keep a fixed and vary c from 0 to a, the resulting ellipses will vary in shape.
Case (i) When c = 0, both foci merge together with the centre of the ellipse and 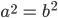 , i.e., a = b, and so the ellipse becomes circle (Fig 11.24 )Thus, circle is a special case of an ellipse .
, i.e., a = b, and so the ellipse becomes circle (Fig 11.24 )Thus, circle is a special case of an ellipse . 
Case (ii) When c = a, then b = 0. The ellipse reduces to the line segment F1F2 joining the two foci (Fig 11.25)
Eccentricity The eccentricity of an ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse (eccentricity is denoted by e i.e 
Then since the focus is at a distance of c from the centre, in terms of the eccentricity the focus is at a distance of ae from the centre.
Standard Equations of an Ellipse: The equation of an ellipse is simplest if the centre of the ellipse is at the origin and the foci are on the x-axis or y-axis. The two such possible orientations are shown in Fig 11.26

Note: From the equation of the ellipse obtained above, it follows that for every point P (x, y) on the ellipse, we get
Therefore, the ellipse lies between the lines x = – a and x = a and touches these lines. Similarly, the ellipse lies between the lines y = – b and y = b and touches these lines
we can also derive the equation of the ellipse as 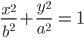
These two equations are known as standard equations of the ellipses.
Note : The standard equations of ellipses have centre at the origin and the major and minor axis are coordinate axes. However, the study of the ellipses with centre at any other point, and any line through the centre as major and the minor axes passing through the centre and perpendicular to major axis are beyond the scope here.
From the Standard Equations of the Ellipses we have the following Observations:
1. Ellipse is symmetric with respect to both the coordinate axes since if (x, y) is a point on the ellipse, then (– x, y), (x, –y) and (– x, –y) are also points on the ellipse.
2. The foci always lie on the major axis. The major axis can be determined by finding the intercepts on the axes of symmetry. That is, major axis is along the x-axis if the coefficient of  has the larger denominator and it is along the y-axis if the coefficient of
has the larger denominator and it is along the y-axis if the coefficient of  has the larger denominator.
has the larger denominator.
Latus Rectum: Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose end points lie on the ellipse Fig 11.28.
To Find the Length of the Latus Rectum of the Ellipse: 
Let the length of 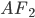 be l. Then the coordinates of A are (c, l ),i.e.,(ae,l)
be l. Then the coordinates of A are (c, l ),i.e.,(ae,l)
Since the ellipse is symmetric with respect to y-axis (of course, it is symmetric w.r.t. both the coordinate axes),  and so length of the latus rectum is
and so length of the latus rectum is
Example: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the latus rectum of the ellipse . 
Since denominator of  is larger than the denominator of
is larger than the denominator of  ,the major axis is along the x-axis. Comparing the given equation with
,the major axis is along the x-axis. Comparing the given equation with  , we get a = 5 and b = 3. Also
, we get a = 5 and b = 3. Also
 = 4
= 4
Hyperbola
Hyperbola: A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant. The term “difference” that is used in the definition means the distance to the farther point minus the distance to the closer point. The two fixed points are Called the Foci of the Hyperbola.
The mid-point of the line segment joining the foci is called the centre of the hyperbola. The line through the foci is called the transverse axis and the line through the centre and perpendicular to the transverse axis is called the conjugate axis. The points at which the hyperbola intersects the transverse axis are called the vertices of the hyperbola (Fig 11.29).
We denote the distance between the two foci by 2c, the distance between two vertices (the length of the transv

erse axis) by 2a and we define the quantity b as
 also 2b is the length of the conjugate axis (Fig 11.30)
also 2b is the length of the conjugate axis (Fig 11.30)
Eccentricity: Just like an ellipse, the ratio e = c/a is called the eccentricity of the hyperbola. Since c ≥ a, the eccentricity is never less than one. In terms of the eccentricity, the foci are at a distance of ae from the centre.
Standard Equation of Hyperbola: The equation of a hyperbola is simplest if the centre of the hyperbola is at the origin and the foci are on the x-axis or y-axis. The two such possible orientations are shown in Fig 11.31

The Equation of Hyperbola with Origin (0,0) and Transverse Axis :

These two equations are known as the standard equations of hyperbolas.
Note: A hyperbola in which a = b is called an equilateral hyperbola.
The standard equations of hyperbolas have transverse and conjugate axes as the coordinate axes and the centre at the origin. However, there are hyperbolas with any two perpendicular lines as transverse and conjugate axes, but the study of such cases will be dealt in higher classes.
From the standard equation of hyperbola ,we have find observations :
- Hyperbola is symmetric with respect to both the axes, since if (x, y) is a point on the hyperbola, then (– x, y), (x, – y) and (– x, – y) are also points on the hyperbola.
- The foci are always on the transverse axis. It is the positive term whose denominator gives the transverse axis.
For example,  has transverse axis along x-axis of length 6, while
has transverse axis along x-axis of length 6, while  has transverse axis along y-axis of length 10.
has transverse axis along y-axis of length 10.
Mensuration Questions from Previous Year Exam
Quiz-summary
0 of 50 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
Information
Mensuration
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 50 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Answered
- Review
-
Question 1 of 50
1. Question
1 pointsThe number of revolutions made by a bicycle wheel 56 cm in diameter in covering a distance of 1.1 km is
Correct
Number of revolutions =

Circumstance of wheel =
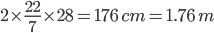
No. of revolutions =
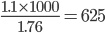 Incorrect
Incorrect
Number of revolutions =

Circumstance of wheel =
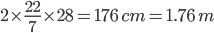
No. of revolutions =
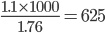
-
Question 2 of 50
2. Question
1 pointsThe area of a circular field is 13.86 hectare. The cost of fencing it @ Rs. 0.60/m is
Correct
A =
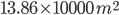
=

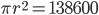

R = 210
Length of fence =
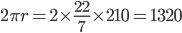
Cost =
 Incorrect
Incorrect
A =
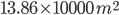
=

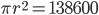

R = 210
Length of fence =
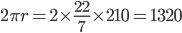
Cost =

-
Question 3 of 50
3. Question
1 pointsThe base of an isosceles triangle is 8 cm and its perimeter is 18 cm. The area of triangle is
Correct
a + a + 8 = 18
 a = 5
a = 5
DC =
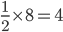
 is a right triangle. Hence
is a right triangle. Hence
 h = 3
h = 3Area of
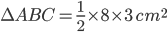
=
 Incorrect
Incorrect
a + a + 8 = 18
 a = 5
a = 5
DC =
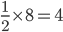
 is a right triangle. Hence
is a right triangle. Hence
 h = 3
h = 3Area of
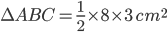
=

-
Question 4 of 50
4. Question
1 pointsEach square of a chess board has an area of
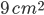 . Also the chess board has a margin of 3 cm around it. The side of the chess board isCorrect
. Also the chess board has a margin of 3 cm around it. The side of the chess board isCorrect
Side of each square of chess board =
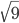
= 3 cm
Side of board =
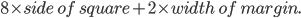
Side of board =

= 24 + 6 = 30 cm
Incorrect
Side of each square of chess board =
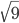
= 3 cm
Side of board =
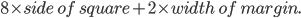
Side of board =

= 24 + 6 = 30 cm
-
Question 5 of 50
5. Question
1 pointsThe area of the quadratic of a circle whose circumference is 22 cm is
Correct


Area quadrant =
 Incorrect
Incorrect


Area quadrant =

-
Question 6 of 50
6. Question
1 pointsIf AB = 12 cm and BC = 5 cm the area of the shaded portion is (use
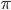 = 3.14)
= 3.14) Correct
Correct
BD =
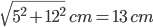
Also BD is diameter
 r = 6.5 cm
r = 6.5 cmRequired = Area of circle – area of rectangle
=
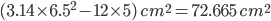 Incorrect
Incorrect
BD =
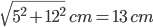
Also BD is diameter
 r = 6.5 cm
r = 6.5 cmRequired = Area of circle – area of rectangle
=
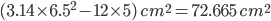
-
Question 7 of 50
7. Question
1 pointsPQRS is diameter of a circle of radius 6 cm such that PQ = OR = RS. Semicircles are drawn on PQ and QS as diameter as shown in figure. Area of the shaded region is
 Correct
Correct
Required area = area semicircle PS + area semicircle PQ – area semicircle QS
=
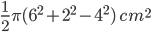
=
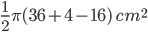
=
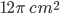 Incorrect
Incorrect
Required area = area semicircle PS + area semicircle PQ – area semicircle QS
=
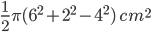
=
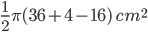
=
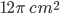
-
Question 8 of 50
8. Question
1 pointsA rectangular field has area equal to
 and perimeter 50 m. Its length and breadth respectively must beCorrect
and perimeter 50 m. Its length and breadth respectively must beCorrect
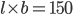
And 2(l + b) = 50
 l + b = 25
l + b = 25Clearly l = 15, b = 10
Incorrect
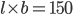
And 2(l + b) = 50
 l + b = 25
l + b = 25Clearly l = 15, b = 10
-
Question 9 of 50
9. Question
1 pointsA rectangular park is 46 m by 36 m. A path 2 m wide is built all around outside it. The cost of constructing these paths @ Rs. 50 per
 isCorrect
isCorrect
Area of path =
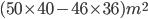
=

Cost = Rs.

= Rs. 17,200
Incorrect
Area of path =
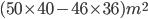
=

Cost = Rs.

= Rs. 17,200
-
Question 10 of 50
10. Question
1 pointsThe length of hypotenuse of a right angled triangle is 5 cm and its area is 6
 . The lengths of the remaining sides areCorrect
. The lengths of the remaining sides areCorrect
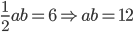

Use a + b =
 Incorrect
Incorrect
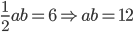

Use a + b =

-
Question 11 of 50
11. Question
1 pointsThe perimeter of a triangle is 450 m and its sides are in the ratio 13 : 12 : 5. The area of the triangle is
Correct
13x + 12 x + 5x = 450
X = 15
A = 195
B = 180
C = 75
Area =
 Incorrect
Incorrect
13x + 12 x + 5x = 450
X = 15
A = 195
B = 180
C = 75
Area =

-
Question 12 of 50
12. Question
1 pointsA circle has area which is 100 times the area of another circle. The ratio of their circumferences is
Correct

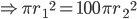

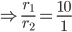

 Incorrect
Incorrect

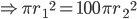

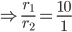


-
Question 13 of 50
13. Question
1 pointsFour equal circles of radius 7 cm touch each other as shown in figure. The area of the shaded part is
 Correct
Correct
Join centres to obtain a square of side 14 cm.
Incorrect
Join centres to obtain a square of side 14 cm.
-
Question 14 of 50
14. Question
1 pointsThe number of square tiles of side 20 cm are required to pave a footpath 1 m wide around a rectangular plot
 isCorrect
isCorrect
Area of foot path =
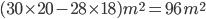

Number of tiles =
 Incorrect
Incorrect
Area of foot path =
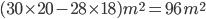

Number of tiles =

-
Question 15 of 50
15. Question
1 pointsIf each side of a rectangle is increased by 50%, its area will increase by
Correct
Original area =

New area =
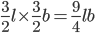
Increase % =

= 125%
Incorrect
Original area =

New area =
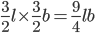
Increase % =

= 125%
-
Question 16 of 50
16. Question
1 pointsCircular disc of area
 is given. With its radius as diameter a circular disc of area
is given. With its radius as diameter a circular disc of area  is cut out of it. The area of the remaining disc is denoted by
is cut out of it. The area of the remaining disc is denoted by  . ThenCorrect
. ThenCorrect
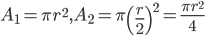
 Incorrect
Incorrect
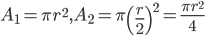

-
Question 17 of 50
17. Question
1 pointsA circular ground has a radius of 26 m. A 4 m wide road runs on the outside around it. The area of the road is (use
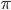 = 3.14)Correct
= 3.14)Correct
Area of road = 3.14
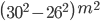
= 3.14 (30 + 26) (30 – 26)

= 703.36

 Incorrect
Incorrect
Area of road = 3.14
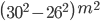
= 3.14 (30 + 26) (30 – 26)

= 703.36


-
Question 18 of 50
18. Question
1 pointsDiagonals of a rhombus are in the ratio 3 : 4 and its area is 2400
 . Side of the rhombus isCorrect
. Side of the rhombus isCorrect

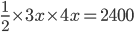

Use : side =
 Incorrect
Incorrect

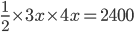

Use : side =

-
Question 19 of 50
19. Question
1 pointsAC is a diameter of circle with centre O. If BD
 at O and OA = 7 cm. Area of shaded region is
at O and OA = 7 cm. Area of shaded region is Correct
Correct
Required area = Area of smaller circle +

=

=
 Incorrect
Incorrect
Required area = Area of smaller circle +

=

=

-
Question 20 of 50
20. Question
1 pointsO is the centre of bigger circle and AC its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm, find area of shaded region.
 Correct
Correct
AC = 54 cm; BC = 10 cm
 AB = (54 – 10) cm = 44 cm
AB = (54 – 10) cm = 44 cmRadius of larger circle = 27 cm
Radius of smaller circle = 22 cm
Required area =

=
 Incorrect
Incorrect
AC = 54 cm; BC = 10 cm
 AB = (54 – 10) cm = 44 cm
AB = (54 – 10) cm = 44 cmRadius of larger circle = 27 cm
Radius of smaller circle = 22 cm
Required area =

=

-
Question 21 of 50
21. Question
1 pointsTwo card boards pieces in form of equilateral triangles having a side of 3 cm each are symmetrically glued to form a regular star as shown in the figure. The area of the star is
 Correct
Correct
Area of star =

is an equilateral triangle with each side equal to 1 cm.
 Incorrect
Incorrect
Area of star =

is an equilateral triangle with each side equal to 1 cm.

-
Question 22 of 50
22. Question
1 pointsABC is an equilateral
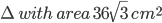 . The area of the inscribed circle isCorrect
. The area of the inscribed circle isCorrect
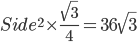
 side = 12 cm
side = 12 cmSemi-Perimeter =
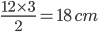
Use r =
 Incorrect
Incorrect
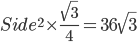
 side = 12 cm
side = 12 cmSemi-Perimeter =
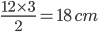
Use r =

-
Question 23 of 50
23. Question
1 pointsThe length of one diagonal of a rhombus is 80% of the other diagonal. The area of the rhombus is how many times the square of the length of the longer diagonal?
Correct
Let the length of the longer diagonal be L.
 Length of shorter diagonal = 80% of L =
Length of shorter diagonal = 80% of L = 
Area of rhombus =

 Incorrect
Incorrect
Let the length of the longer diagonal be L.
 Length of shorter diagonal = 80% of L =
Length of shorter diagonal = 80% of L = 
Area of rhombus =


-
Question 24 of 50
24. Question
1 pointsOABC is a rhombus whose vertices A, B and C lie on a circle with centre at O. If radius of circle is 10 cm then area of the rhombus
Correct
OA = OB = OC = AB = BC = 10 cm
Clearly
 are both equilateral and also congruent.
are both equilateral and also congruent.
Then area Rhombus =

=
 Incorrect
Incorrect
OA = OB = OC = AB = BC = 10 cm
Clearly
 are both equilateral and also congruent.
are both equilateral and also congruent.
Then area Rhombus =

=

-
Question 25 of 50
25. Question
1 points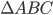 is an equilateral triangle with area
is an equilateral triangle with area  . With each vertex as centre a circle is described with radius equal to half the length of the said of the triangle. [Use
. With each vertex as centre a circle is described with radius equal to half the length of the said of the triangle. [Use 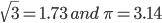 ] The area of the shaded part is
] The area of the shaded part is Correct
Correct
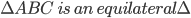
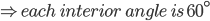
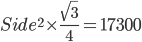
Side = 200 m
Radius of each circle = 100 m
Shaded area = area of
 - 3(area of any sector).Incorrect
- 3(area of any sector).Incorrect
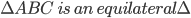
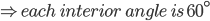
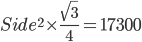
Side = 200 m
Radius of each circle = 100 m
Shaded area = area of
 - 3(area of any sector).
- 3(area of any sector). -
Question 26 of 50
26. Question
1 pointsIf both radius and heights of a cone are increased by 50%, then the volume of the cone will increase by
Correct


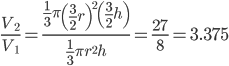
Volume increasing by
 Incorrect
Incorrect


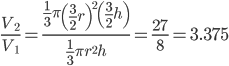
Volume increasing by

-
Question 27 of 50
27. Question
1 pointsIf both the height and the radius of the cone are doubled, then the ratio of volume of the bigger cone to that of the smaller cone will be
Correct

 Incorrect
Incorrect


-
Question 28 of 50
28. Question
1 pointsA cylindrical tub of radius 12 cm contains water to the height of 20 cm. A spherical iron ball is dropped into the tub. The ball gets completely immersed and the level of water is raised by 6.75 cm. The radius of the ball is
Correct
Radius of ball : r = ?; Radius of tube : R = 12 cm
H = 6.75 cm
Volume of ball = Volume of cylinder ABCD


 r= 9 cmIncorrect
r= 9 cmIncorrect
Radius of ball : r = ?; Radius of tube : R = 12 cm
H = 6.75 cm
Volume of ball = Volume of cylinder ABCD


 r= 9 cm
r= 9 cm -
Question 29 of 50
29. Question
1 pointsDiameter of a roller 60 m long is 42 cm. If it takes 700 complete revolutions to level a pay ground, the cost of leveling the play ground @ 45 p per square m is nearly
Correct
h = 42 cm; r = 30 cm, n = 700
Area leveled =

=
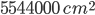
=
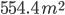
Cost = Rs.
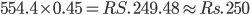 Incorrect
Incorrect
h = 42 cm; r = 30 cm, n = 700
Area leveled =

=
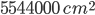
=
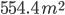
Cost = Rs.
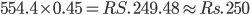
-
Question 30 of 50
30. Question
1 points2 cubes of each of side 12 cm are joined end to end. Volume of the resulting cuboid is
Correct

L = 24 cm, B = 12 cm, H = 12 cmV =
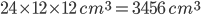 Incorrect
Incorrect

L = 24 cm, B = 12 cm, H = 12 cmV =
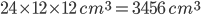
-
Question 31 of 50
31. Question
1 pointsA circus tent is cylindrical up to a height of 5 m and conical above it. If its diameter is 105 m and slant height of the conical portion is 53 m. The area of the canvas used to build the tent is
Correct
r =
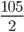 m; l = 53 m
m; l = 53 mH = 3 m

Area of canvas= C.S.A. cone + C.S.A. of cylindrical
=

=

=

=
 Incorrect
Incorrect
r =
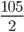 m; l = 53 m
m; l = 53 mH = 3 m

Area of canvas= C.S.A. cone + C.S.A. of cylindrical
=

=

=

=

-
Question 32 of 50
32. Question
1 pointsA solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and diameter of the cylinder is 7 cm. The S.A. of the solid is
Correct
r =

H + 2r = 19 cm
 h = 12 cm
h = 12 cm

Surface area =
=

=

=
 Incorrect
Incorrect
r =

H + 2r = 19 cm
 h = 12 cm
h = 12 cm

Surface area =
=

=

=

-
Question 33 of 50
33. Question
1 pointsThe radius of a sphere is increased by 100%, then the increase in surface area of the sphere will be
Correct
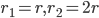

Increase in area = 300%
Incorrect
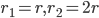

Increase in area = 300%
-
Question 34 of 50
34. Question
1 pointsDiameter of a cooper sphere is 6 cm. The sphere is melted and drawn into a wire of uniform circular cross section which is 72 cm long. The diameter of the wire is nearly
Correct
Volume of wire (cylinder) = Volume of sphere
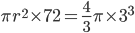


=

 Incorrect
Incorrect
Volume of wire (cylinder) = Volume of sphere
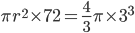


=


-
Question 35 of 50
35. Question
1 pointsThree cubes of edges 12 cm, 16 cm and 20 cm are melted and a new cube is made. The side of the new cube is
Correct

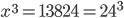
Side of new cube =24 cm
Incorrect

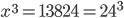
Side of new cube =24 cm
-
Question 36 of 50
36. Question
1 pointsThe cost of white washing the four walls of a room is Rs. 100. The cost of white washing a room twice in length and breadth but one fourth in height is
Correct
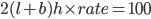

 required cost = Rs. 50Incorrect
required cost = Rs. 50Incorrect
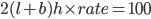

 required cost = Rs. 50
required cost = Rs. 50 -
Question 37 of 50
37. Question
1 pointsThe volume of a cylinder is
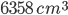 and its height is 28 cm. Its curved surface area isCorrect
and its height is 28 cm. Its curved surface area isCorrect


C.S.A. =
 Incorrect
Incorrect


C.S.A. =

-
Question 38 of 50
38. Question
1 pointsA hemispherical bowl is made of steel 12.1 cm thick. The inside radius of the bowl is 5 cm. The volume of steel used in making the bowl is nearly
Correct
r = 5 cm
R = (5 + 2.1) cm = 7.1
Volume of material =

=

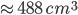 Incorrect
Incorrect
r = 5 cm
R = (5 + 2.1) cm = 7.1
Volume of material =

=

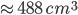
-
Question 39 of 50
39. Question
1 pointsA spherical balloon was deflated till its radius was halved. If its volume becomes n times its original volume then value of n is
Correct

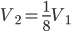 Incorrect
Incorrect

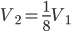
-
Question 40 of 50
40. Question
1 pointsThree cubes of edges 12 cm, 16 cm and 20 cm are melted and a new cube is made. The diagonal of the new cube is
Correct

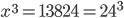
 Side of new cube = 24 cm
Side of new cube = 24 cm Incorrect
Incorrect

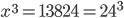
 Side of new cube = 24 cm
Side of new cube = 24 cm
-
Question 41 of 50
41. Question
1 pointsA rectangular sheet of area
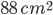 and length 8 cm is rolled along its breadth to make a hollow cylinder. The volume of this cylinder isCorrect
and length 8 cm is rolled along its breadth to make a hollow cylinder. The volume of this cylinder isCorrect
Circumference of cylinder = 88 cm
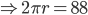

Also h = 8
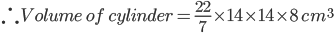
=
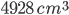 Incorrect
Incorrect
Circumference of cylinder = 88 cm
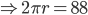

Also h = 8
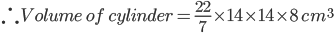
=
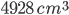
-
Question 42 of 50
42. Question
1 pointsCurved surface area of a cone whose volume is
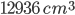 and the diameter of base is 42 cm, isCorrect
and the diameter of base is 42 cm, isCorrect
r =



L =

C.S.A. =

=
 Incorrect
Incorrect
r =



L =

C.S.A. =

=

-
Question 43 of 50
43. Question
1 pointsIf each side of a cube is tripped then its volume increases by
Correct
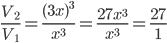
Increse in vol =
 = 27 -1 = 26
= 27 -1 = 26 increase % = 2600%Incorrect
increase % = 2600%Incorrect
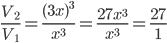
Increse in vol =
 = 27 -1 = 26
= 27 -1 = 26 increase % = 2600%
increase % = 2600% -
Question 44 of 50
44. Question
1 pointsA spherical ball was melted and made into smaller balls of half the radius of the original. The ratio of the sum total of the surface of all the smaller balls to that of the original ball is
Correct
Number of small balls =
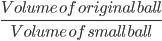
=

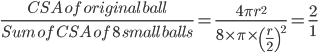
Or 2 : 1
Incorrect
Number of small balls =
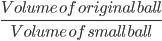
=

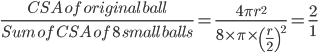
Or 2 : 1
-
Question 45 of 50
45. Question
1 pointsA cooper sphere of diameter 6 cm is drawn into a wire of diameter 0.4 cm. The length of the wire is
Correct
Volume wire (cyl) =Vol. of sphere
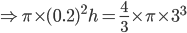
 Incorrect
Incorrect
Volume wire (cyl) =Vol. of sphere
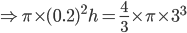

-
Question 46 of 50
46. Question
1 pointsRadii of two cylinder are in ratio 4 : 3 and their heights are in ratio 3 : 4. Ratio of their volumes is
Correct
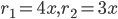

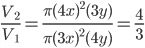 Incorrect
Incorrect
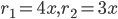

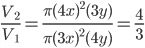
-
Question 47 of 50
47. Question
1 pointsThe curved surface area of a cylinder is
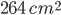 and its volume is
and its volume is 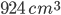 . The height of the cylinder isCorrect
. The height of the cylinder isCorrect

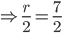


 Incorrect
Incorrect

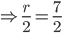



-
Question 48 of 50
48. Question
1 pointsThe circumference of edge of a hemispherical bowl is 132 cm. Its capacity is
Correct


Volume =
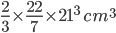
=
 Incorrect
Incorrect


Volume =
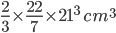
=

-
Question 49 of 50
49. Question
1 pointsThe radii of two right circular cylinder are in ratio 2 : 3 and their heights are in ratio 5 : 4. The ratio of their curved surface areas is
Correct
 Incorrect
Incorrect

-
Question 50 of 50
50. Question
1 pointsA vessel is in form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the base of the hemispherical bowl is 6 cm and the total height of the vessel is 11 cm. The capacity of the vessel is (Use
 = 3.14)Correct
= 3.14)Correct
r = 3 cm
H = (11 – 3) cm = 8 cm
Capacity of vessel =
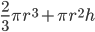
=

=

=

=
 Incorrect
Incorrect
r = 3 cm
H = (11 – 3) cm = 8 cm
Capacity of vessel =
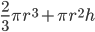
=

=

=

=







0 Comments