Logarithm Solved Examples - Page 3
Logarithm Important Questions - Page 4
Logarithm Video Lecture - Page 5
Logarithm, in mathematics is the exponent or power to which a stated number called base , is raised to yield a specific number. For example on the expression  , the Logarithm of 100 to the base 10 is 2. This is written as
, the Logarithm of 100 to the base 10 is 2. This is written as 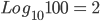 Logarithms were originally invented to help simplify the arithmetical processes of multiplication, division, expansion to a power and extraction of a 'root', but they are now a days used for variety of purposes in pure and applied mathematics.
Logarithms were originally invented to help simplify the arithmetical processes of multiplication, division, expansion to a power and extraction of a 'root', but they are now a days used for variety of purposes in pure and applied mathematics.
If for a positive real number (a ≠ 1) , 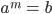 , then the index m is called the Logarithm of b to the base a.
, then the index m is called the Logarithm of b to the base a.
We write this as: 
Log begins the abbreviation of the word ‘Logarithm’. Thus 
Where  = b is called the exponential form and
= b is called the exponential form and 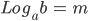 is called the Logarithmic form.
is called the Logarithmic form.
Exponential Form
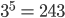


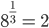
Logarithmic Form
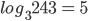
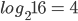
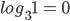

Logarithm Shortcut Method and Formulas
- Product Formula: The Logarithm of the product of two numbers is equal to the sum of their Logarithms.
i.e.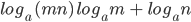
Generalisation: In general, we have
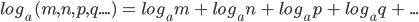
- Quotient formula: The Logarithm of the quotient of two numbers is equal of their Logarithm.
i.e. . Where a, m, n are positive and a ≠ 1
. Where a, m, n are positive and a ≠ 1 - Power formula: The Logarithm of a number raised to a power is equal to the power multiplied by Logarithm of the number.
i.e. . Where a, m are positive and a ≠ 1
. Where a, m are positive and a ≠ 1 - Base changing formula:
 Where m, n, a are positive and n ≠ 1, a ≠ 1.
Where m, n, a are positive and n ≠ 1, a ≠ 1. - Reciprocal Relation:
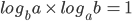 , where a, b are positive and not equal to 1
, where a, b are positive and not equal to 1 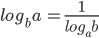
 , where a and x are positive and a ≠ 1
, where a and x are positive and a ≠ 1- If a > 1 and x > 1, then
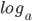 x > 0.
x > 0. - If 0 < a < 1 and 0 < x < 1, then
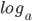 x > 0.
x > 0. - If 0 < a < 1 and x > 1, then then
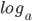 x > 0.
x > 0. - if a > 1 and 0 < x < 1, then then
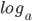 x < 0.
x < 0. - Logarithm of 1 to any base is equal to zero. i.e.
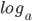 1 = 0, where a > 0, a ≠ 1
1 = 0, where a > 0, a ≠ 1 - Logarithm of any number to the same base is 1. i.e.
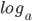 a = 1, where a > 0, a ≠ 1
a = 1, where a > 0, a ≠ 1 - Common logarithms: There are two base of logarithms that are extensively used these days. One is base e(e=2.71828 approx) and the other is base 10. The logarithms to base 10 are called the common logarithms.
AND
Logarithm Solved Questions
Example 1: 
Answer: 3
Solution: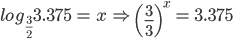

Example 2: If  find yz(2 - x).
find yz(2 - x).
Answer: 1
Solution: yz(2 - x) = 2yz - xyz = 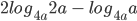
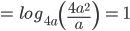
Example 3: 
Answer: 1
Solution: Each is equal to k
 log x = k(l + m - 2n),
log x = k(l + m - 2n),
log y = k(m + n - 2l), log z = k(n + l - 2m),
 log xyz = k(0)
log xyz = k(0)  xyz =
xyz =  = 1 =
= 1 =  = 1
= 1
Example 4: If log 
Answer: 23
Solution: ![log\left ( \frac{x + y}{5} \right )\, =\, \, \frac{1}{2}\left [ log\, x + log\, y \right ]](https://questionpaper.org/wp-content/plugins/latex/cache/tex_3f47be09d4ad61a6b6f567dcc5caec7e.gif)
x + y = ![\sqrt[5]{xy}\Rightarrow x^{2}\, +\, y^{2}\, =\, 23xy](https://questionpaper.org/wp-content/plugins/latex/cache/tex_a87b947d865e56e0a446ff06623e0a72.gif)
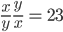
Example 5: If log (x + y) = log  , then log x - log y =
, then log x - log y =
Answer: Log 5
Solution: x + y = 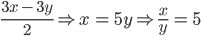
log x - log y = log 5
Logarithm Questions from Previous Year Exams.
- Logarithm Aptitude
Logarithm Online Study Material - Video Tutorial





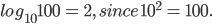

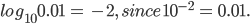
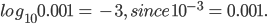

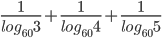

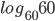



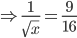
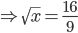

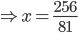


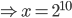





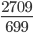







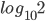
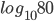

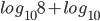








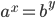

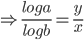

0 Comments