When quantities of different kinds are connected to one another so that we know how much of one quantity is equivalent to a given quantity of a second, etc. We can determine how much of the last kind is equivalent to a given of first kind by the chain rule.
Proportion and Indirect Proportion
If increase or decrease of a quantity 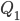 causes increase or decrease of another quantity
causes increase or decrease of another quantity  in the same extent then,
in the same extent then, 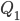 is directly proportional to
is directly proportional to 
1) Number of persons  Amount of work done, i.e. more persons, more work
Amount of work done, i.e. more persons, more work
2) Number of days  Amount of work, i.e. more days, more work
Amount of work, i.e. more days, more work
3) Working rate 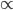 Amount of work, i.e. more working rate, more work
Amount of work, i.e. more working rate, more work
4) Efficiency of man 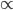 Amount of work, i.e. more efficiency of man, more work
Amount of work, i.e. more efficiency of man, more work
Combining I,II,III,and IV,  Amount of work. If increase of a quantity
Amount of work. If increase of a quantity 
5) Number of men  , i.e. more the men, less the no. of days required
, i.e. more the men, less the no. of days required
Chain Rule Important Formulas
1) 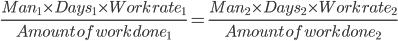
Remember, “Man days” required per unit work is always same. In fact,  specify the volume of job or work.
specify the volume of job or work.
2) If in place of men there are engines burning coal for certain number of hours, then, the above equation changes to

Because, here the job of engine is to burn the coal.
3) If number of examiners examining a number of answer books in number of days by working a number of hours or day, since the job of examiner is to check the answer books,
then, 
Chain Rule Solved Examples and Solutions
Question 1) A garrison of 3000 men has provisions for 25 days, when given at the rate of 900 g per head. At the end of 11 days, a reinforcement arrives and it was found that now the provision will last 10 days more, when given at the rate of 840 g per head. What is the strength of reinforcement ? (MBA, ’82)
Solution : Let strength of reinforcement be x
Remaining food provisions after 11 days =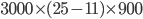
Total men after 11 days=(3000+x)
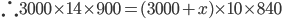
 x=1,500.
x=1,500.
 The reinforcement had 1,500 men.
The reinforcement had 1,500 men.
Question 2) Six diesel engines consume 900 litres of diesel, when each one is running for 5 h a day. How much diesel will be required by 9 engines, each running 8 h a day when 5 diesel engines of former type consume as much diesel as 8 diesel engines of the latter type.
Solution : Using the formula,

Since 5 diesel engines of I type=8 diesel engines of II type

 = ?
= ?
(Since Amount of work = Diesel consumption)

 =1,350 litres.
=1,350 litres.
 The diesel required is 1,350 litres
The diesel required is 1,350 litres
Question 3) Two coal loading machines each working 12 hours per day for 8 days handles 9,000 tonnes of coal with an efficiency of 90%. While 3 other coal loading machines at an efficiency of 80% set to handle 12,000 tonnes of coal in 6 days. Find how many hours per day each should work.
Solution: Here 
=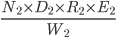


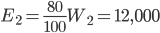
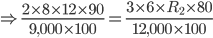
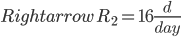
 Each machine should work
Each machine should work 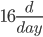
Question 4) ’A’ can do a piece of work in 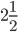 days which ‘B’ can do in
days which ‘B’ can do in  days. If ‘A’ wages are Rs.50 per week and ‘B’ wages are Rs.42.50 per week, what ‘A’ would have charged for doing a piece of work for which B received Rs 340? (ITI, ’90)
days. If ‘A’ wages are Rs.50 per week and ‘B’ wages are Rs.42.50 per week, what ‘A’ would have charged for doing a piece of work for which B received Rs 340? (ITI, ’90)
Solution : Total wage = Total Amount of work; Wage rate = work Rate
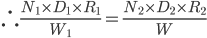

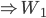 = 300
= 300
 ‘A’ should charge Rs 300 for the job.
‘A’ should charge Rs 300 for the job.
Question 5) Four lorries carrying 4 tons each move 128 tons in 8 days. In how many days will 6 tons in 8 days. In how many days will 6 lorries carrying 3 tons each move 540 tons ?
Solution : 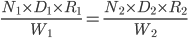
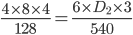
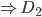 = 30 days.
= 30 days.
Chain Rule Questions from previous year exams
Quiz-summary
0 of 18 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
Information
chain rule aptitude
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 18 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- Answered
- Review
-
Question 1 of 18
1. Question
1 pointsIf 6 women can reap 60 hectares in 24 days, then how many hectares can 36 women reap in 30 days ?
Correct
More women, More hectares
More days, More hectaresWomen 6 : 36 } :: 60 : z
Days 24 : 30z =
 = 450
= 450450 hectares
Incorrect
More women, More hectares
More days, More hectaresWomen 6 : 36 } :: 60 : z
Days 24 : 30z =
 = 450
= 450450 hectares
-
Question 2 of 18
2. Question
1 pointsIf the price of 8 toys is Rs. 288.64, what will be the approximate price of 7 toys?
Correct
Let the required price be Rs. z . Then, Less cost
Therefore, 8 : 7 :: 288.64 : z
8z = 7
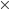 288.64
288.64 ⇒ z = 252.56
Incorrect
Let the required price be Rs. z . Then, Less cost
Therefore, 8 : 7 :: 288.64 : z
8z = 7
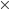 288.64
288.64 ⇒ z = 252.56
-
Question 3 of 18
3. Question
1 pointsA certain number of persons can dig a trench 150 m long, 60 m broad and 15 m deep in 20 days. The same number of persons can dig another trench 25 m broad and 20 m deep in 30 days. The length of the second trench is :
Correct
More broad, Less length [Indirect proportion]
More deep, Less length [Indirect proportion]
More days, More length [Direct proportion]
Broad 25 : 60 } :: 150 : z
Deep 20 : 15
Days 20 : 30z =
 = 405 mIncorrect
= 405 mIncorrect
More broad, Less length [Indirect proportion]
More deep, Less length [Indirect proportion]
More days, More length [Direct proportion]
Broad 25 : 60 } :: 150 : z
Deep 20 : 15
Days 20 : 30z =
 = 405 m
= 405 m -
Question 4 of 18
4. Question
1 pointsIf 90 lamps can be lighted, 8 hours per day for 20 days for Rs. 19.5, then the number of lamps, which can be lighted 6 hours daily for 25 days, for Rs. 58.5, is:
Correct
Let the required number of lamps be z.
Less hours per day, More lamps
More money, More lamps
More days, Less lamps
Rs. 19.5 : 58.5 } :: 90 : z
Days 25 : 20z =
 = 288 lampsIncorrect
= 288 lampsIncorrect
Let the required number of lamps be z.
Less hours per day, More lamps
More money, More lamps
More days, Less lamps
Rs. 19.5 : 58.5 } :: 90 : z
Days 25 : 20z =
 = 288 lamps
= 288 lamps -
Question 5 of 18
5. Question
1 pointsA machine weaves 0.75 m of cloth every second. Approximately, how many seconds will it take for the weave 20 m of cloth?
Correct
Let the required time be z seconds. Then,
More meters, More time (Direct proportion)
Therefore, 0.75 : 20 : : 1 : z
0.75z = 20 × 1 ⇒ z = 26.6
So. the approx time is 26 sec.
Incorrect
Let the required time be z seconds. Then,
More meters, More time (Direct proportion)
Therefore, 0.75 : 20 : : 1 : z
0.75z = 20 × 1 ⇒ z = 26.6
So. the approx time is 26 sec.
-
Question 6 of 18
6. Question
1 pointsThe cost of 15 Bags of salt, each weighing 915 grams is Rs. 18. What will be the cost of 25 Bags, if each bag weight is 1 kg?
Correct
More bags, More cost
More weight, More cost
Bags 15 : 25 } :: 18 : z
Weighing 915 : 1000
Therefore, (15 x 915 x z) = (25 x 1000 x 18) So, the Rs. is 32.78.
Incorrect
More bags, More cost
More weight, More cost
Bags 15 : 25 } :: 18 : z
Weighing 915 : 1000
Therefore, (15 x 915 x z) = (25 x 1000 x 18) So, the Rs. is 32.78.
-
Question 7 of 18
7. Question
1 pointsOn a scale of map, 0.5 cm represents 5.5 km. If the distance between the points on the map is 25.5 cm, the actual distance between these points is :
Correct
Let the actual distance be z km. Then,
More distance on the map, More is the actual distance (Direct proportion)Therefore, 0.5 : 25.5 : 5.5 : z
0.5 z = 25.5 × 5.5 ⇒ z =
 ⇒ z = 280.5 kgIncorrect
⇒ z = 280.5 kgIncorrect
Let the actual distance be z km. Then,
More distance on the map, More is the actual distance (Direct proportion)Therefore, 0.5 : 25.5 : 5.5 : z
0.5 z = 25.5 × 5.5 ⇒ z =
 ⇒ z = 280.5 kg
⇒ z = 280.5 kg -
Question 8 of 18
8. Question
1 pointsA flagstaff 12.5 m high casts a shadow of length 36.5 m. The height of the building, which casts a shadow of length 18.75 m under similar conditions will be:
Correct
Let the height of the building be z meters. Then,
Less lengthy shadow, Less is the height (direct proportion)Therefore, 36.5 : 18.75 :: 12.5 : z
36.5 z = 18.75 x 12.5 ⇒ z = 6.42 m
Incorrect
Let the height of the building be z meters. Then,
Less lengthy shadow, Less is the height (direct proportion)Therefore, 36.5 : 18.75 :: 12.5 : z
36.5 z = 18.75 x 12.5 ⇒ z = 6.42 m
-
Question 9 of 18
9. Question
1 points30 men can complete a piece of work in 15 days. In how many days will 25 men complete the same work?
Correct
Let the required number of days be z . Then,
Less men , More days (Indirect proportion)Therefore, 25 : 30 :: 15 : z
25 z = 30 x 15 ⇒ z = 18 days
Incorrect
Let the required number of days be z . Then,
Less men , More days (Indirect proportion)Therefore, 25 : 30 :: 15 : z
25 z = 30 x 15 ⇒ z = 18 days
-
Question 10 of 18
10. Question
1 pointsRunning at the same constant rate, 5 identical machines can produce a total of 250 mugs per minute. At this rate, how many mugs could 10 such machines produce in 5 minutes?
Correct
Let the required number of mugs be z. Then,
More machine, More mugs
More minutes, more mugs
Machines 5 : 10 } :: 250 : z
Minute 1 : 5
So, 5 x 1 x z = 250 x 10 x 5 ⇒ z = 2500.Incorrect
Let the required number of mugs be z. Then,
More machine, More mugs
More minutes, more mugs
Machines 5 : 10 } :: 250 : z
Minute 1 : 5
So, 5 x 1 x z = 250 x 10 x 5 ⇒ z = 2500. -
Question 11 of 18
11. Question
1 points15 boys working 9 hours per day complete a piece of work in 12 days. To complete the same work in 5 days, working 18 hours a day, the number of boys required, is :
Correct
Let the required number of men be z.
Less days, More boys
More working hrs per day, Less boysDays 5 : 12 } :: 15 : z
Hours 18 : 9
= 18 Boys.Incorrect
Let the required number of men be z.
Less days, More boys
More working hrs per day, Less boysDays 5 : 12 } :: 15 : z
Hours 18 : 9
= 18 Boys. -
Question 12 of 18
12. Question
1 points12 boys, working 3 hours a day can complete a work in 20 days. How many hours a day must 18 boys work to complete the same work in 10 days?
Correct
More boys, Less hours per day
Less days, More hours per dayBoys 18 : 12 } :: 3 : z
Days 10 : 20so z = 4 hrs
Incorrect
More boys, Less hours per day
Less days, More hours per dayBoys 18 : 12 } :: 3 : z
Days 10 : 20so z = 4 hrs
-
Question 13 of 18
13. Question
1 points27 people can repair a building in 15 days, working 4 hours a day. In how many days will 20 people, working 9 hours a day, complete the work?
Correct
Let the required number of days be z. Then,
Less people, More days
More working hours per day, Less daysPeople 20 : 27 } :: 15 : z
Hours 9 : 4 z = 9daysIncorrect
Let the required number of days be z. Then,
Less people, More days
More working hours per day, Less daysPeople 20 : 27 } :: 15 : z
Hours 9 : 4 z = 9days -
Question 14 of 18
14. Question
1 points5 Taps, working 8 hours a day, can empty a water tank in 3 days. How many hours a day must 6 taps work to empty the tank in 1 day?
Correct
More Taps, Less working hours per day
Less days, More working hours per dayTaps 6 : 36 } :: 8 : z
Days 1 : 3z z = 20 hrs.Incorrect
More Taps, Less working hours per day
Less days, More working hours per dayTaps 6 : 36 } :: 8 : z
Days 1 : 3z z = 20 hrs. -
Question 15 of 18
15. Question
1 pointsIf 8 boys or 12 girls can do a piece of work in 28 days, then in how many days will 4 boys and 8 girls do the same work?
Correct
Let required number of days be z. Then,
Since, 8 boys = 12 girls, therefore,
(4 boys & 8 girls) = (6 girls + 8 boys) = 14 girls
⇒ 14 : 12 :: 28 : z
z =
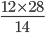 = = 24daysIncorrect
= = 24daysIncorrect
Let required number of days be z. Then,
Since, 8 boys = 12 girls, therefore,
(4 boys & 8 girls) = (6 girls + 8 boys) = 14 girls
⇒ 14 : 12 :: 28 : z
z =
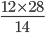 = = 24days
= = 24days -
Question 16 of 18
16. Question
1 points54 pumps can empty a reservoir in 21/3 days, working 5 hours a day. If 216 pumps are used for 3 hours each day, then the same work will be completed in :
Correct
Let the required number of days be z. Then,
More pumps, Less days
Less working hours/day, More days
Pumps 216 : 54
Hours 3 : 5z = 3.67 days
Incorrect
Let the required number of days be z. Then,
More pumps, Less days
Less working hours/day, More days
Pumps 216 : 54
Hours 3 : 5z = 3.67 days
-
Question 17 of 18
17. Question
1 points20 laborers, working 7 hours a day can finish a piece of work in 30 days. If the laborers work 5 hours a day, then the number of labourers to finish the same piece of work in 40 days, will be :
Correct
Let the required number of laborers be x. then,
Less working hrs/ Day, More laborers
More days, Less laborers
Hours 5 : 7 } :: 20 : z
Days 40 : 30z =
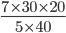 = 21 daysIncorrect
= 21 daysIncorrect
Let the required number of laborers be x. then,
Less working hrs/ Day, More laborers
More days, Less laborers
Hours 5 : 7 } :: 20 : z
Days 40 : 30z =
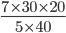 = 21 days
= 21 days -
Question 18 of 18
18. Question
1 pointsIf 8 carpenters, working 5 hours a day, can make 350 chairs in 24 days. How many chairs will 12 carpenters make in 36 days, each working 8 hours a day?
Correct
Let required number of be z. Then,
More carpenters, More chairs
More hours per day, More chairs
More days, More chairs
Carpenters 8 : 12 } :: 350 : z
Hours 5 : 8
Days 24 : 36z =
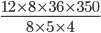 = 1260 chairsIncorrect
= 1260 chairsIncorrect
Let required number of be z. Then,
More carpenters, More chairs
More hours per day, More chairs
More days, More chairs
Carpenters 8 : 12 } :: 350 : z
Hours 5 : 8
Days 24 : 36z =
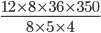 = 1260 chairs
= 1260 chairs
Chain Rule Important Videos - Must Watch




0 Comments