Least Common Multiple (LCM) & Highest Common Factor(H.C.F)
Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of all the numbers.
Example: LCM of 3 and 4 = 12 because 12 is the smallest multiple which is common to 3 and 4 (In other words, 12 is the smallest number which is divisible by both 3 and 4)
LCM Example and Shortcuts
How to find out LCM using prime factorization method
We can find LCM using prime factorization method in the following steps
Step1 : Express each number as a product of prime factors.
Step2 : LCM = The product of highest powers of all prime factors
Example 1 : Find out LCM of 8 and 14
Step1 : Express each number as a product of prime factors. (Reference: Prime Factorization and how to find out Prime Factorization)

14 = 2 χ 7
Step2 : LCM = The product of highest powers of all prime factors
Here the prime factors are 2 and 7
The highest power of 2 here = 
The highest power of 7 here = 7
Hence LCM =  χ 7
χ 7
Example 2 : Find out LCM of 18, 24, 9, 36 and 90
Step1 : Express each number as a product of prime factors (Reference: Prime Factorization and how to find out Prime Factorization).
18 = 2 χ 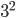
24 =  χ 3
χ 3
9 = 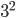
36 =  χ
χ 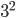
90 = 2 χ 5 χ 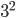
Step2 : LCM = The product of highest powers of all prime factors
Here the prime factors are 2, 3 and 5
The highest power of 2 here = 
The highest power of 3 here = 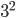
The highest power of 5 here = 5
Hence LCM =  χ
χ 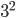 χ 5 = 360
χ 5 = 360
Hence Least common multiple (L.C.M) of 18, 24, 9, 36 and 90 = 2 × 2 × 3 × 3 × 2 × 5 = 360
How to find out LCM using Division Method (shortcut)
Step 1 : Write the given numbers in a horizontal line separated by commas.
Step 2 : Divide the given numbers by the smallest prime number which can exactly divide at least two of the given numbers.
Step 3 : Write the quotients and undivided numbers in a line below the first.
Step 4 : Repeat the process until we reach a stage where no prime factor is common to any two numbers in the row.
Step 5 : LCM = The product of all the divisors and the numbers in the last line.
Example 1 : Find out LCM of 8 and 14
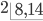

Example 2 : Find out LCM of 18, 24, 9, 36 and 90


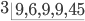


Hence Least common multiple (L.C.M) of 8 and 14 = 2 × 4 × 7 = 56
HCF Example and Shortcuts Tricks
Highest Common Factor (H.C.F) or Greatest Common Measure(G.C.M) or Greatest Common Divisor (G.C.D) of two or more numbers is the greatest number which divides each of them exactly.
Example : HCF or GCM or GCD of 60 and 75 = 15 because 15 is the highest number which divides both 60 and 75 exactly.
How to find out HCF using prime factorization method
Step1 : Express each number as a product of prime factors. (Reference: Prime Factorization and how to find out Prime Factorization)
Step2 : HCF is the product of all common prime factors using the least power of each common prime factor.
Example 1 : Find out HCF of 60 and 75 (Reference: Prime Factorization and how to find out Prime Factorization)
Step1: Express each number as a product of prime factors.


Step2: HCF is the product of all common prime factors using the least power of each common prime factor.
Here, common prime factors are 3 and 5
The least power of 3 here = 3
The least power of 5 here = 5
Hence, HCF = 3 × 5 = 15
Example 2 : Find out HCF of 36, 24 and 12
Step1 : Express each number as a product of prime factors. (Reference: Prime Factorization and how to find out Prime Factorization)
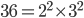


Step2 : HCF is the product of all common prime factors using the least power of each common prime factor.
Here 2 and 3 are common prime factors.
The least power of 2 here = 
The least power of 3 here = 3
Hence, HCF = 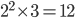
Example 3 : Find out HCF of 36, 27 and 80
Step1 : Express each number as a product of prime factors. (Reference: Prime Factorization and how to find out Prime Factorization)
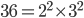


Step2 : HCF = HCF is the product of all common prime factors using the least power of each common prime factor.
Here you can see that there are no common prime factors.
Hence, HCF = 1
How to find out HCF using prime factorization method - By dividing the numbers (shortcut)
Step 1 : Write the given numbers in a horizontal line separated by commas.
Step 2 : Divide the given numbers by the smallest prime number which can exactly divide all of the given numbers.
Step 3 : Write the quotients in a line below the first.
Step 4 : Repeat the process until we reach a stage where no common prime factor exists for all of the numbers.
Step 5 :We can see that the factors mentioned in the left side clearly divides all the numbers exactly and they are common prime factors. Their product is the HCF
Example 1 : Find out HCF of 60 and 75



We can see that the prime factors mentioned in the left side clearly divides all the numbers exactly and they are common prime factors. no common prime factor is exists for the numbers came at the bottom.
Hence HCF = 3 χ 5 = 15
Example 2 : Find out HCF of 36, 24 and 12




We can see that the prime factors mentioned in the left side clearly divides all the numbers exactly and they are common prime factors. no common prime factor is exists for the numbers came at the bottom.
Hence HCF = 2 × 2 × 3 = 12.
How to calculate LCM and HCF for fractions
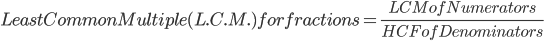
Example 1: Find out LCM of 
LCM = 
Example 2: Find out LCM of 
LCM =  =
= 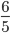
Highest Common Multiple (H.C.F) for fractions
HCF for fractions = 
Example 1: Find out HCF of 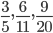
HCF =  =
= 
Example 2: Find out HCF of  ,
, 
HCF =  =
= 
How to calculate LCM and HCF for Decimals
Step 1 : Make the same number of decimal places in all the given numbers by suffixing zero(s) in required numbers as needed.
Step 2 : Now find the LCM/HCF of these numbers without decimal.
Step 3 : Put the decimal point in the result obtained in step 2 leaving as many digits on its right as there are in each of the numbers.
Example1 : Find the LCM and HCF of .63, 1.05, 2.1
Step 1 : Make the same number of decimal places in all the given numbers by suffixing zero(s) in required numbers as needed.
i.e., the numbers can be writtten as .63, 1.05, 2.10
Step 2 : Now find the LCM/HCF of these numbers without decimal.
Without decimal, the numbers can be written as 63, 105 and 210 .
LCM (63, 105 and 210) = 630
HCF (63, 105 and 210) = 21
Step 3 : Put the decimal point in the result obtained in step 2 leaving as many digits on its right as there are in each of the numbers.
i.e., here, we need to put decimal point in the result obtained in step 2 leaving two digits on its right.
i.e., the LCM (.63, 1.05, 2.1) = 6.30
HCF (.63, 1.05, 2.1) = .21
LCM and HCF Problems from Previous Year Questions
Quiz-summary
0 of 38 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
Information
This chapter realated to LCM and HCF.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 38 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- Answered
- Review
-
Question 1 of 38
1. Question
1 pointsTwo numbers are in the ratio 3 : 4 and the product of their LCM and HCF is 10800. What will be the sum of the numbers?
Correct
Let the numbers be 3x and 4x respectively.
10800 = 3x
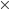 4x
4x x2 = 900
x2 = 900 x = 30
x = 30Sum of the numbers = 3x + 4x = 7x
= 7
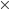 30 = 210Incorrect
30 = 210Incorrect
Let the numbers be 3x and 4x respectively.
10800 = 3x
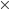 4x
4x x2 = 900
x2 = 900 x = 30
x = 30Sum of the numbers = 3x + 4x = 7x
= 7
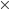 30 = 210
30 = 210 -
Question 2 of 38
2. Question
1 pointsThe LCM of two numbers is 2079 and their HCF is 27. If one of the numbers is 189, find the other.
Correct
Let the x = The other number:
HCF =

27 =

189X =
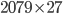
 X =
X = 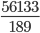
 X = 297
X = 297Hence theother number is 297
Incorrect
Let the x = The other number:
HCF =

27 =

189X =
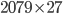
 X =
X = 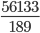
 X = 297
X = 297Hence theother number is 297
-
Question 3 of 38
3. Question
1 pointsThe greatest number of six digits which when divided by 6, 7, 8, 9 and 10 gives 4, 5, 6, 7 and 8 respectively as remainder, is
Correct
Greatest number of six digits = 999999
LCM of 6, 7, 8, 9 and 10 = 2520
On dividing 999999 by 2520, remainder - 2079
Since,6 - 4 = 7 - 5 = 8 - 6 = 9 - 7 = 10 - 8 = 2
therefore, The greatest number = (999999 - 2079) - 2 = 997918
Incorrect
Greatest number of six digits = 999999
LCM of 6, 7, 8, 9 and 10 = 2520
On dividing 999999 by 2520, remainder - 2079
Since,6 - 4 = 7 - 5 = 8 - 6 = 9 - 7 = 10 - 8 = 2
therefore, The greatest number = (999999 - 2079) - 2 = 997918
-
Question 4 of 38
4. Question
1 pointsThe smallest number of five digits which on being divided by 4, 5, 6 and 7 leaves 3, 4, 5 and 6 respectively as remainder, is.
Correct
Smallest number of five digits = 10000
LCM of 4, 5, 6 and 7 = 420
On dividing 10000 by 420, remainder = 340
Since, 4 - 3 = 5 - 4 = 6 - 5 = 7 - 6 = 1
Therefore, The smallest number = (10000 + 420) - 340 - 1 = 10079
Incorrect
Smallest number of five digits = 10000
LCM of 4, 5, 6 and 7 = 420
On dividing 10000 by 420, remainder = 340
Since, 4 - 3 = 5 - 4 = 6 - 5 = 7 - 6 = 1
Therefore, The smallest number = (10000 + 420) - 340 - 1 = 10079
-
Question 5 of 38
5. Question
1 points when expressed in lowest terms isCorrect
when expressed in lowest terms isCorrect
H.C.F. of 444 and 629 is 37.
On dividing Numerator and Denominator by 37, we get =
 Incorrect
Incorrect
H.C.F. of 444 and 629 is 37.
On dividing Numerator and Denominator by 37, we get =

-
Question 6 of 38
6. Question
1 pointsThe smallest number which when diminished by 3 is divisible by 21, 28, 36 and 45 is
Correct
Number =(L.c.m. of 21, 28, 36, 45) + 3 = 1260 + 3 = 1263
Incorrect
Number =(L.c.m. of 21, 28, 36, 45) + 3 = 1260 + 3 = 1263
-
Question 7 of 38
7. Question
1 pointsWhat is the least number which when divided by 8,9,12 and 15 leaves the same remainder 1 in each case .[C.B.l. 1993]
Correct
Required number = (L.C.M. of 8, 9, 12, 15) + 1 = 360 + 1 = 361.
Incorrect
Required number = (L.C.M. of 8, 9, 12, 15) + 1 = 360 + 1 = 361.
-
Question 8 of 38
8. Question
1 pointsThe traffic lights at three different road crossings change after every 48 sec, 72 sec and 108 sec respectively. If they all change simultaneously at 8 : 20 : 00 hours, then they will again change simultaneously at (C.D.T. 1992)
Correct
Interval of change = (L.C.M of 48,72,108)sec = 432sec.
So, the lights will agin change simultaneously after every 432 seconds i.e,7 min.12sec
Hence , next simultaneous change will take place at 8:27:12 hrs.
Incorrect
Interval of change = (L.C.M of 48,72,108)sec = 432sec.
So, the lights will agin change simultaneously after every 432 seconds i.e,7 min.12sec
Hence , next simultaneous change will take place at 8:27:12 hrs.
-
Question 9 of 38
9. Question
1 pointsFind the greatest number which on dividing 1657 and 2037 leaves remainders 6 and 5 respectively.
Correct
Required number = H.C.F of (1657 - 6) and (2037 - 5) = H.C.F of 1661 and 2032.
1651 ) 2032 ( 1 1651 381 ) 1651 ( 4 1524 127) 381 ( 3 381 x Incorrect
Required number = H.C.F of (1657 - 6) and (2037 - 5) = H.C.F of 1661 and 2032.
1651 ) 2032 ( 1 1651 381 ) 1651 ( 4 1524 127) 381 ( 3 381 x -
Question 10 of 38
10. Question
1 pointsFind the largest number of four digits exactly divisible by 12. 15, 18, 27.(SBI 2000)
Correct
The largest number of four digits is 9999.
Required number must be divisible by L.C.M of 12, 15, 18, 27 i.e, 540.
On dividing 9999 by 540, we get 279 as remainder .
∴ Required number = (9999 - 279) = 9720.
Incorrect
The largest number of four digits is 9999.
Required number must be divisible by L.C.M of 12, 15, 18, 27 i.e, 540.
On dividing 9999 by 540, we get 279 as remainder .
∴ Required number = (9999 - 279) = 9720.
-
Question 11 of 38
11. Question
1 pointsFind the H.C.F and L.C.M of 2, 8, 16 and 10 .398127
Correct
H.C.F of given fractions =
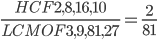
LCM of given fractions =
 Incorrect
Incorrect
H.C.F of given fractions =
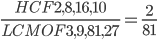
LCM of given fractions =

-
Question 12 of 38
12. Question
1 pointsThe H.C.F of two number is 11 . and their L.C.M is 693. If one of the numbers is 77, find the other.
Correct
In this type of problems ,remembered
Product of two numbers = Product of their HCF and LCM
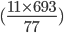 = 99Incorrect
= 99Incorrect
In this type of problems ,remembered
Product of two numbers = Product of their HCF and LCM
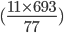 = 99
= 99 -
Question 13 of 38
13. Question
1 pointsFind the L.C.M of 72, 108 and 2100.
Correct

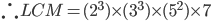 = 37800Incorrect
= 37800Incorrect

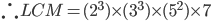 = 37800
= 37800 -
Question 14 of 38
14. Question
1 pointsFind the least number which when divided by 20, 25, 35 and 40 leaves remainders 14, 19, 29 and 34 respectively.
Correct
Here, (20 – 14) = 6, (25 – 19) = 6, (35 – 29) = 6 and (40 – 34) = 6.
∴ Required number = (L.C.M. of 20, 25, 35, 40) – 6 = 1394.
Incorrect
Here, (20 – 14) = 6, (25 – 19) = 6, (35 – 29) = 6 and (40 – 34) = 6.
∴ Required number = (L.C.M. of 20, 25, 35, 40) – 6 = 1394.
-
Question 15 of 38
15. Question
1 pointsFind the largest number which divides 62, 132 and 237 to leave the same remainder in each case .
Correct
Required number = H.C.F. of (132 – 62), (237 – 132) and (237 – 62)
HC.F. = 70, 105 and 175 = 35.
Incorrect
Required number = H.C.F. of (132 – 62), (237 – 132) and (237 – 62)
HC.F. = 70, 105 and 175 = 35.
-
Question 16 of 38
16. Question
1 pointsFind the least number which when divided by 5, 6, 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder.(IBPS 2001)
Correct
L.C.M. of 5, 6, 7, 8 = 840.
∴ Required number is of the form 840k + 3.
Least value of k for which (840k + 3) is divisible by 9 is k = 2.
∴ Required number = (840 × 2 + 3) = 1683.
Incorrect
L.C.M. of 5, 6, 7, 8 = 840.
∴ Required number is of the form 840k + 3.
Least value of k for which (840k + 3) is divisible by 9 is k = 2.
∴ Required number = (840 × 2 + 3) = 1683.
-
Question 17 of 38
17. Question
1 pointsFind the greatest possible length which can be used to measure exactly the lengths 4m 95cm, 9m and 16m 65cm.
Correct
Required length = H.C.F. of 495 cm, 900 cm, and 1655 cm.
495=

 = 45Incorrect
= 45Incorrect
Required length = H.C.F. of 495 cm, 900 cm, and 1655 cm.
495=

 = 45
= 45 -
Question 18 of 38
18. Question
1 pointsFind the least number which when divided by 6,7,8,9 and 12 leaves the same remainder 1 in each case.
Correct
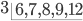



∴ L.C.M. = 3 × 2 × 2 × 7 × 2 × 3 = 504.
Incorrect
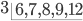



∴ L.C.M. = 3 × 2 × 2 × 7 × 2 × 3 = 504.
-
Question 19 of 38
19. Question
1 pointsThe HCF of the following fractions is
 ,
,  and
and 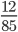 Correct
Correct
HCF of the fractions =
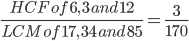 Incorrect
Incorrect
HCF of the fractions =
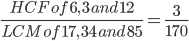
-
Question 20 of 38
20. Question
1 pointsSamantha, Jessica and Roseline begin to jog around a circular stadium. They complete their revolutions in 84 s, 56 s and 63 s , respectively. After how many seconds will they be together at the starting point?
Correct
Incorrect
LCM of 84 s, 56 s and 63 s = 504 s
therefore, After 504 s, they will be together at the starting point.
-
Question 21 of 38
21. Question
1 pointsThree rods of lengths 15 m, 42 m and 39 m are to be cut into pieces of equal length. What is the greatest possible length of each pieces?
Correct
Incorrect
The greatest possible length of
each pieces = HCF of 15 m, 42 m and 39 m
= 3 m -
Question 22 of 38
22. Question
1 pointsFour drums containing water have capacities 135 L, 205 L, l-65 L and 240 L. The greatest capacity measure which can be used to measure the capacities of the drums is.
Correct
Incorrect
The greatest capacity measure = HCF of 135 L, 205 L, 165 L and 240 L
= 5 L
-
Question 23 of 38
23. Question
1 pointsThe least number of square bricks required to make the floor of 150 cm leneth and 125 cm width is.
Correct
Incorrect
Maximum length of the brick = HCF of 150 cm, 125 cm
= 25 cm
 The least number of square bricks =
The least number of square bricks = 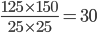
-
Question 24 of 38
24. Question
1 pointsFour bells ring at intervals of 30 min, 1 h, 1
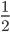 h and 1 h 45 min respectively. AII the bells ring simultaneously at 12 noon. They will again ring simultaneously at..Correct
h and 1 h 45 min respectively. AII the bells ring simultaneously at 12 noon. They will again ring simultaneously at..Correct
Incorrect
LCM of 30 min, 1 h, 1
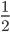 , and 1 h 45 min = 1260 min
, and 1 h 45 min = 1260 min
= 21 h
So, they will again ring simultaneously at 21h i.e., 9 am. -
Question 25 of 38
25. Question
1 pointsA man wants to plant trees in a garden. If the number of trees in each row is the same and there are 35 or 14 or 21 rows, then no tree is left. The least number of trees, the man has, is
Correct
Incorrect
The least number of trees = LCM of 35, 14 and 21
= 210
-
Question 26 of 38
26. Question
1 pointsWhich is the greatest number which will divide 1600 and 1420 exactly?
Correct
Incorrect
The greatest number = HCF of 1600 and 1420
= 20 -
Question 27 of 38
27. Question
1 pointsThe greatest number which on dividing 42, 49 and 56 will leave 6,7 and 8 respectively as remainder, is.
Correct
Incorrect
The greatest number
= HCF of (42 - 6), (49 - 7) and (56 - 8)
= HCF of 36, 42 and,48
= 6 -
Question 28 of 38
28. Question
1 pointsThe greatest number which on dividing 152, 277 and 427 leaves equal remainder, is
Correct
Incorrect
The greatest number
= HCF of (277 - 152) and (427 - 277)
= HCF of 125 and 150
= 25 -
Question 29 of 38
29. Question
1 pointsThe least nurnber which when divided by 9, 11 and 15 leaves 8 as remainder in each case, is
Correct
Incorrect
The least nurmber = (LCM of 9, 11 and 15) + 8
= 495+ 8 = 503 -
Question 30 of 38
30. Question
1 pointsThree numbers are in the ratio 1: 2 : 3 and their H.C.F. is 12. The numbers are: . [CBI 1991]
Correct
Let the required numbers be z, 2z and 3z. Then, their H.C.F. = z. So, z = 12.
The numbers are 12, 24 and 36.Incorrect
Let the required numbers be z, 2z and 3z. Then, their H.C.F. = z. So, z = 12.
The numbers are 12, 24 and 36. -
Question 31 of 38
31. Question
1 pointsAbout the number of pairs which have 16 as their H.C.F. and 136 as their L.C.M., we can definitely say that : .[Cal. 1990]
Correct
H.C.F. of two numbers divides their L.C.M. exactly. Since 16 is not a factor of 136, it states that there does not exist any pair of numbers with H,C.F. 16 and L.C.M. 136.
Incorrect
H.C.F. of two numbers divides their L.C.M. exactly. Since 16 is not a factor of 136, it states that there does not exist any pair of numbers with H,C.F. 16 and L.C.M. 136.
-
Question 32 of 38
32. Question
1 pointsThe greatest number that will divide 187, 233 and 279 leaving the same remainder in each case is . [Central Excise ]
Correct
Required number = H.C.F. of (233 - 187), (279 -233) and (279 - 187)
H.C.F. of 46, 46 and 92 = 46.Incorrect
Required number = H.C.F. of (233 - 187), (279 -233) and (279 - 187)
H.C.F. of 46, 46 and 92 = 46. -
Question 33 of 38
33. Question
1 pointsThe H.C.f. of 1095 and 1168 is:
Correct
divide 1168 by 1095 and then with reminder to 1095 answer should be 0
Incorrect
divide 1168 by 1095 and then with reminder to 1095 answer should be 0
-
Question 34 of 38
34. Question
1 pointsThe smallest number which when diminished by 3 is divisible by 21, 28, 36 and 45 is
Correct
Number =(L.c.m. of 21, 28, 36, 45) + 3 = 1263.
Incorrect
Number =(L.c.m. of 21, 28, 36, 45) + 3 = 1263.
-
Question 35 of 38
35. Question
1 pointsSix bells commence tolling together and toll at intervals of 2, 4, 6, 8, 10 and 12 seconds respectively. In 30 minutes, how many times do they toll together. [C.B.I. 1991]
Correct
L.C.M. of 2, 4, 6, 8, 10, 12 is 120.
So, the bells will toll together after every 120 seconds i.e. 2 minutes.
In 30 minutes, they will toll together in 30/2 + 1 = 16 times.Incorrect
L.C.M. of 2, 4, 6, 8, 10, 12 is 120.
So, the bells will toll together after every 120 seconds i.e. 2 minutes.
In 30 minutes, they will toll together in 30/2 + 1 = 16 times. -
Question 36 of 38
36. Question
1 pointsFind the least number exactly divisible by 12, 15, 20 and 27.
Correct
L.C.M = 3 × 4 × 5 × 9 = 540.
Hence, required number is 540.
Incorrect
L.C.M = 3 × 4 × 5 × 9 = 540.
Hence, required number is 540.
-
Question 37 of 38
37. Question
1 pointsReduce
 to lowest terms.Correct
to lowest terms.Correct
H.C.F of 391 and 667 is 23.
On dividing the numerator and denominator by 23, we get : Incorrect
Incorrect
H.C.F of 391 and 667 is 23.
On dividing the numerator and denominator by 23, we get :
-
Question 38 of 38
38. Question
1 pointsFind the L.C.M of 16, 24, 36 and 54
Correct
L.C.M = 2 × 2 × 2 × 3 × 3 × 2 × 3 = 432.
Incorrect
L.C.M = 2 × 2 × 2 × 3 × 3 × 2 × 3 = 432.
LCM and HCF Problems from Previous Year Questions




Example 1: Find out HCF of 35,611,920
HCF = HCF(3,6,9)HCF(5,11,20) = 3220
Example 2: Find out HCF of 45
, 23
HCF = HCF(4,2)HCF(5,10) = 215
formula is incorrect but solution is correct.
Help me hcf and lcm basic concept long tricks
Find out LCM of 22,12
132
That's 24