Height and Distance Formulas
One of the important applications of trigonometry is in finding the height and distances of the point which are not directly measurable. This is done with the help of trigonometric ratios.
DEFINITIONS

(A) Angle of Elevation
Let
O: Position of the object
A: Position of the height
Here, object (A) is at height level than observer (O)
OX: Reference line (or horizontal line)
OA: Line of sight (or line of observation)
Then
 =
= AOX =angle of elevation
AOX =angle of elevation
Angle of Depression

Let
O: Position of the observer
B: Position of the object
Here, object (B) is at lower level than the observer (O)
OX: Reference line (or horizontal line)
OB: Line of sight (or line of observation)
Then
 =
= BOX =angle of depression
BOX =angle of depression
RESULTS USEFUL IN FINDING HEIGHTS AND DISTANCE

(A) In a right-angle triangle ABC,*
Sin= =
=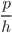
cos= =
=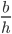
tan= =
=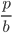
(B) In any triangle ABC,
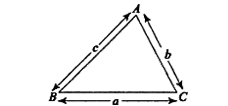
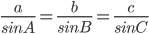 [ Sin Rule ]
[ Sin Rule ]
 = constant (of each side of the angle)
= constant (of each side of the angle)
(C) In any angle ABC
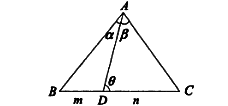
If  and
and
 BAD =
BAD =
 CAD =
CAD =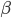
 ADC =
ADC =
Then, (m + n) cot  =m cot
=m cot -n cot
-n cot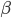
(D) In a right - angle triangle ABC,
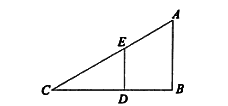
If DE  AB, then
AB, then

Important Examples of Height and Distance
Example 1: A ladder 15 m long just reaches the top of a wall and makes an angle of 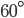 with the wall. Find the distance of the foot of the ladder from the wall.
with the wall. Find the distance of the foot of the ladder from the wall. 
Solution: Let AB be the wall
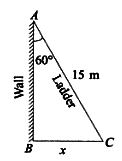
AC = length of ladder = 15m
 BAC = 60
BAC = 60
BC = x = distance of the foot of the ladder from the wall
Then, using the relation,
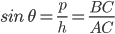

x = 15 =
= 
Example 2: From a tower 125 m high, the angle of depression of a car is  . Find how far the car is from the tower.
. Find how far the car is from the tower.
Solution: Let OT be the tower and C be the position of the car
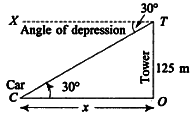
 XTC = angle of depression of car (viewed from T )
XTC = angle of depression of car (viewed from T )
= (given)
(given)
=  TCO (since XT
TCO (since XT CO,)
CO,)
OT = length of tower =125 m
OC = x = distance of the car from the fool of the tower OT
Then, using the relation
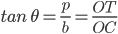
(from time saving, write directly as other leg (x) =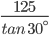 Refer aid to momory of 25.2)
Refer aid to momory of 25.2)

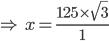 = 216.5
= 216.5
Hence, the required distance is 216.5 m
Example 3: The angle of elevation of the top of a tower 30 m high, from two points on the level ground on its opposite side are  and
and 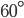 . Find the distance between the two point
. Find the distance between the two point
Solution:
Let OT be the tower
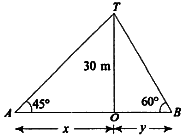
 Height of tower = OT = 30 m
Height of tower = OT = 30 m
Lets A and B be the opposite side of tower OT.
Then, angle of elevation from A =  TAO =
TAO =
and angle of elevation from B =  TBO =
TBO =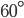
Distance between AB = AO + OB = x + y (say)
Now, in right  ATO,
ATO,
Tan =  =
= 
 x =
x =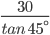 = 30 m
= 30 m
And in right  BTO,
BTO,

 y
y
=
Hence the required distance = x + y = 30 + 17.32 = 47.32 m
Example 4: A balloon leaves the earth at point A and rise at a uniform velocity. At the end of 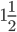 min. An observer situated at a distance of 200 m from A, finds the angular elevation of the balloon to the
min. An observer situated at a distance of 200 m from A, finds the angular elevation of the balloon to the 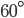 .Find the speed of the balloon.
.Find the speed of the balloon.
Solution:
Let the balloon, after leaving the point A, reach to point B vertically upward in 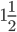 min. The observer situated at point O, observes the angle of elevation of B as
min. The observer situated at point O, observes the angle of elevation of B as 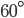
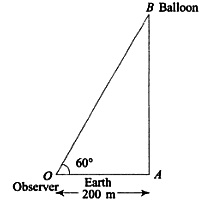
 BOA =
BOA =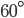
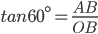
AB = OB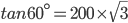 metre Speed of the balloon
metre Speed of the balloon

 metre/sec
metre/sec
=3.87 metre/sec.
Height and Distance Questions from Previous Year Exams
Quiz-summary
0 of 11 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
Information
- Height and Distance Aptitude
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 11 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- Answered
- Review
-
Question 1 of 11
1. Question
1 pointsA man watching from the top of a tower a boat speeding away from the tower.The boat makes an angle of depression of
 with the man's eye when at a distance of 60 metres from the tower.After 5 seconds,the angle of depression becomes
with the man's eye when at a distance of 60 metres from the tower.After 5 seconds,the angle of depression becomes  .What is the approximate speed of the boat,assuming.That it is running in still water ?(S.B.I.P.O.1999)Correct
.What is the approximate speed of the boat,assuming.That it is running in still water ?(S.B.I.P.O.1999)Correct
Let AB be the tower and C and D be the two positions of the boats.
Then,

Let AB = h.
Then,

And,
 m.
m. CD=(AD-AC)=(60
CD=(AD-AC)=(60  m.
m.Hence,required speed=

=
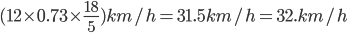 Incorrect
Incorrect
Let AB be the tower and C and D be the two positions of the boats.
Then,

Let AB = h.
Then,

And,
 m.
m. CD=(AD-AC)=(60
CD=(AD-AC)=(60  m.
m.Hence,required speed=

=
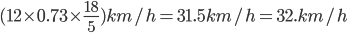
-
Question 2 of 11
2. Question
1 pointsA man on the top of a vertical observation,tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angles of depression to change from 30
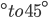 ,how soon after this will the car reach the observation tower ?Correct
,how soon after this will the car reach the observation tower ?Correct
Let AB be the tower and C and D be the two positions of the car.
Then,
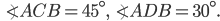
Let, AB=h, CD=x and AC=y.

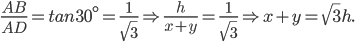
 x=(x+y)-y=
x=(x+y)-y= 
Now,
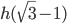 is covered in 12 min.
is covered in 12 min.SO, h will be covered in
![\left[\frac{12}{(\sqrt{3}-1)}\times h\right]=\frac{12}{(\sqrt{3}-1)}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_636e4ccb87cab7ff8bee30624b4a8b75.gif)
=
 min=16 min.23 secIncorrect
min=16 min.23 secIncorrect
Let AB be the tower and C and D be the two positions of the car.
Then,
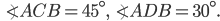
Let, AB=h, CD=x and AC=y.

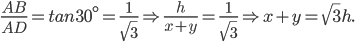
 x=(x+y)-y=
x=(x+y)-y= 
Now,
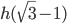 is covered in 12 min.
is covered in 12 min.SO, h will be covered in
![\left[\frac{12}{(\sqrt{3}-1)}\times h\right]=\frac{12}{(\sqrt{3}-1)}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_636e4ccb87cab7ff8bee30624b4a8b75.gif)
=
 min=16 min.23 sec
min=16 min.23 sec -
Question 3 of 11
3. Question
1 pointsThe top of a 15 metre high tower makes an angle of elevation of
 with the bottom of an electric pole and angle of elevation
with the bottom of an electric pole and angle of elevation  with the top of the pole. What is the height of the electric pole ?Correct
with the top of the pole. What is the height of the electric pole ?Correct
Let, AB be the tower and CD be the electric pole.
Then,
 and AB=15 m.
and AB=15 m.Let, CD=h.Then,BE=(AB-AE)=(AB-CD)=(15-h)

And,
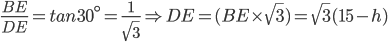
AC=DE
 (15-h)
(15-h)
 h = 10 m.Incorrect
h = 10 m.Incorrect
Let, AB be the tower and CD be the electric pole.
Then,
 and AB=15 m.
and AB=15 m.Let, CD=h.Then,BE=(AB-AE)=(AB-CD)=(15-h)

And,
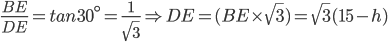
AC=DE
 (15-h)
(15-h)
 h = 10 m.
h = 10 m. -
Question 4 of 11
4. Question
1 pointsThe angle of elevation of the sun, when the length of the shadow of a tree 3 times the height of the tree, is:
Correct
Let AB be the tree and AC be its shadow
Let

Then ,
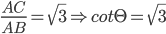
 Incorrect
Incorrect
Let AB be the tree and AC be its shadow
Let

Then ,
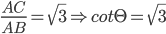

-
Question 5 of 11
5. Question
1 pointsFrom a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:(bank p.o 1999)
Correct
Let AB be the tower.
Then ,
 and AB = 100 m
and AB = 100 m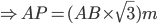
=

= (100 x 1.73) m
= 173 m.Incorrect
Let AB be the tower.
Then ,
 and AB = 100 m
and AB = 100 m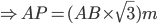
=

= (100 x 1.73) m
= 173 m. -
Question 6 of 11
6. Question
1 pointsAn observer 1.6 m tall is 20
 away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The heights of the tower is:Correct
away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The heights of the tower is:Correct
Let AB be the observer and CD be the tower.
Draw BE perpendicular CD.
Then, CE = AB = 1.6 m,

 m = 20 m
m = 20 m CD = CE + DE = (1.6 + 20) m = 21.6 m.Incorrect
CD = CE + DE = (1.6 + 20) m = 21.6 m.Incorrect
Let AB be the observer and CD be the tower.
Draw BE perpendicular CD.
Then, CE = AB = 1.6 m,

 m = 20 m
m = 20 m CD = CE + DE = (1.6 + 20) m = 21.6 m.
CD = CE + DE = (1.6 + 20) m = 21.6 m. -
Question 7 of 11
7. Question
1 pointsThe angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
Correct
Let AB be the wall and BC be the ladder.
Then ,
 and AC = 6.4 m
and AC = 6.4 m
 BC = 2 x AC
BC = 2 x AC= (2 x 4.6) m
= 9.2 m.Incorrect
Let AB be the wall and BC be the ladder.
Then ,
 and AC = 6.4 m
and AC = 6.4 m
 BC = 2 x AC
BC = 2 x AC= (2 x 4.6) m
= 9.2 m. -
Question 8 of 11
8. Question
1 pointsA man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?(s.b.i 1990)
Correct
One of AB, AD and CD must have given.
So, the data is inadequate.
Incorrect
One of AB, AD and CD must have given.
So, the data is inadequate.
-
Question 9 of 11
9. Question
1 pointsTwo ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30º and 45º respectively. If the lighthouse is 100 m high, the distance between the two ships is(bank p.o 2001)
Correct
Let AB be the lighthouse and C and D be the positions of the ships.
Then, AB = 100 m
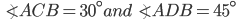
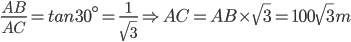
 AD = AB = 100 m
AD = AB = 100 m CD = (AC + AD) =
CD = (AC + AD) = 
=
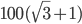
= (100 x 2.73) m
= 273 m.Incorrect
Let AB be the lighthouse and C and D be the positions of the ships.
Then, AB = 100 m
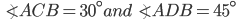
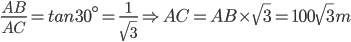
 AD = AB = 100 m
AD = AB = 100 m CD = (AC + AD) =
CD = (AC + AD) = 
=
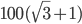
= (100 x 2.73) m
= 273 m. -
Question 10 of 11
10. Question
1 pointsThe angle of elevation of the top of a tower from a certain point is
 .If the observer moves 20 m towards the tower,the angle of elevation of the top of the tower increases by
.If the observer moves 20 m towards the tower,the angle of elevation of the top of the tower increases by  .The height of the tower is :Correct
.The height of the tower is :Correct
Let AB be the tower and C and D be the points of observation.then
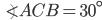 ,
,  AND CD=20 m
AND CD=20 m
Let AB =h.
Then,
And,
CD=20
 h=
h=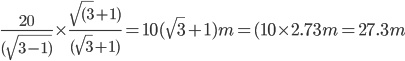 Incorrect
Incorrect
Let AB be the tower and C and D be the points of observation.then
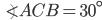 ,
,  AND CD=20 m
AND CD=20 m
Let AB =h.
Then,
And,
CD=20
 h=
h=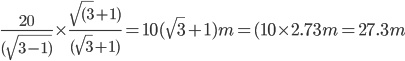
-
Question 11 of 11
11. Question
1 pointsOn the same side of a tower ,two objects are located.observed from the top of the tower,their angles of depression are
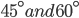 . If the height of the tower is 150 m the distance between the objects is :Correct
. If the height of the tower is 150 m the distance between the objects is :Correct
Let,s AB be the tower and C and D be the objects.
Then,AB=150 m,
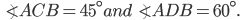
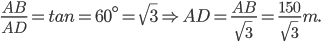

 CD=(AC-AD)
CD=(AC-AD)=
![(150-\frac{150}{\sqrt{3}})m=\left [\frac{150\sqrt{3}-1}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \right ]m=50(3-\sqrt{3})m=(50\times 1.27)m=63.5m](https://questionpaper.org/wp-content/plugins/latex/cache/tex_e9b2e0902d5fd4e6e02cecd636206511.gif) Incorrect
Incorrect
Let,s AB be the tower and C and D be the objects.
Then,AB=150 m,
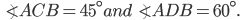
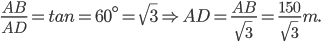

 CD=(AC-AD)
CD=(AC-AD)=
![(150-\frac{150}{\sqrt{3}})m=\left [\frac{150\sqrt{3}-1}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \right ]m=50(3-\sqrt{3})m=(50\times 1.27)m=63.5m](https://questionpaper.org/wp-content/plugins/latex/cache/tex_e9b2e0902d5fd4e6e02cecd636206511.gif)
Hint
Height and Distance Important Video




0 Comments