PRIME NUMBERS : A prime number is a a counting number greater then 1, which is divisible only by 1 and by itself. For example: 2, 3, 5, 7, 11, etc.
PERFECT SQUARE : A whole number whose square root is also a whole number is called a perfect square. For example: 4, 9, 16, etc.
PERFECT CUBE : A whole number whose cube root is also a whole number is called a perfect cube. For example: 1, 8, 27, 64, etc.
Arithmetic Progression (AP)/ Arithmetic Series
An arithmetic progression is the sequence of numbers in which a number in the series is obtained by adding a constant number to the previous number in the series.
The sum of first n terms of the series s=n2{2a+(n−1)d}
Where a is the first term and d is the common difference.
The sum of the series (of all n terms)
= n2{a+l}=n2{2a+(n−1)d}
Where ‘a’ is the first term and ‘l’ is the last term
For example,
2, 5, 8, 11 ……. n common difference = 3
9, 15, 21, 27………. n common difference = 6
Geometric Progression (GP) / Geometric Series
A sequence of numbers is said to be in geometric progression (GP), if the ratio of two consecutive terms in the sequence is always the same and is called the common ratio. The nth term of a series is given by
an=a. rn−1
l=a. rN−1
Sn=a(rn−1)/(r−1)
SN=a(rN−1)/(r−1),r≠1
Where,
a = first term sn = Sum of first n terms
r = common ratio sN = Sum of all N terms of the series
l = last term
For examples
3, 15, 75, 375, ………. n common ratio = 5
2,6, 18, 54 ………. common ratio = 3
Combination Series
This can be series combing different rules in a logical way.
(a) Series of perfect squares: For example 9, 25, 49, 81, 121………
The series can be represented by the mathematical expression f(x)=(1+2x)2
Where x = 1, 2, 3
(b) Series of perfect cubes : For example,
(i) 1, 27, 729, 19683……..
Can be represented by f(x)=(27)x−1
Where x=1,2,3,4
(ii) 1, 64, 373, 1000…
Can be represented by fx=[1+3(x−1)]3
Where x = 1, 2, 3, 4…..
Second Degree Arithmetic Series
A series in which the differences between the successive terms themselves are in AP and forms an arithmetic series is called the second degree arithmetic series.
For example, 2, 3, 6, 11, 18……
A series in which the differences between the successive terms themselves are in AP and forms an arithmetic series is called the second degree arithmetic series.
For example, 2, 3, 6, 11, 18……
The Difference of successive terms of the above series 1, 3, 5, 7..... which forms an arithmetic series with common difference 2.
The given series can be represented by a quadratic mathematics function: f(x)=x2+2
Where x =0, 1, 2, 3, 4…….
Third Degree Arithmetic Series
A series in which the difference of the successive terms forms a second degree arithmetic series is termed third degree arithmetic series. Mathematically, such a series can be represented by a general cubic function and hence the name third degree.
For example:
(a) 20, 30, 42, 59, 84, 120, 170,…
The difference of successive terms of the above series is 2, 5, 11, 14… and this forms an arithmetic series with common difference 3.
(b) 1, 15, 53, 127,249, 431, 685,……
The difference of successive terms of the above series is 14, 38, 74, 122, 182, 254. The difference of successive terms of the above series is 24, 36, 48, 60, 72 and this forms an arithmetic series with common difference 12.
Mathematically, the given series can be represented by a cubic function
f(x)=2x3−2
Where x = 1, 2, 3, 4…..
Arithmetic-Geometric (A-G) Series
The series is formed by combination of arithmetic progressions. Each succeeding term is obtained by first adding ( or subtracting) the common difference of its AP to the previous term and then multiplying (or dividing) the sum by common ratio of its GP. An important property of such an A-G series is that the difference of successive terms is in GP.
For example: 1, 8, 22, 50, 106, 218
Series is obtained by adding 3 to previous term and then multiplying the sum by 2.
i.e a2=(a1+3)×2
Geometric Arithmetic (G-A) Series
Each succeeding term in G-A series is funded by first multiplying(or dividing)
the previous term by the common ratio of its GP and then adding (or subtracting) to it the common difference of its AP. This important property of G-A series, like A-G series, is that the difference of its successive terms are in geometric progression.
For example: 1, 2, 6, 22, 86, 342,..
The terms in the above series are obtained by fist multiplying the previous term by 4 and then subtracting 2 from the resultant product.
Twin Series
As the name suggests, it consists of two series combined into a single series. The alternating terms of this series form an independent series.
For example: 2, 3, 7, 9, 12, 27, 17, 81, 22, 243…..
Odd terms of the series 2, 7, 12, 22,…… is an arithmetic series with common difference 5. Even terms of the series 3, 9, 27, 81, 243….. is a geometric series with common ratio 3.
Alternating Series
In an alternating series, the successive terms increase and decrease alternately. It differs from irregular increase (or decrease) series wherein the successive terms increase (or decrease) continuously but the ratio of increase does not follow a particular trend. While solving an alternate series we should focus on the following possibility of its formation:
1) Whether it is a twin series which has been formed by combining two different series.
2) It has been formed by performing two different kinds of operations alternately on successive terms.
For example: 6, 13, 12, 40, 24, 104, 48, 229, 96…
In the above series, there are two series 6, 12, 24, 48, 96…and 13, 40, 104,229...i.e. the fist one is a geometric series with first term 6 and common ratio 2.
In the second series, terms are having difference 27, 64, 125…. i.e…, 33,45,53
Odd Man Out (Wrong Number) in a Series
For example:
3, 5, 7, 9, 11…. 9 is the odd man out because all others are prime numbers.
2, 3, 7, 10, 11… Except 10, all are prime numbers.
3, 10, 29, 66, 127, 220, 345….. Except 220, all other terms can be expressed as x3+2, where x = 1, 2, 3…..
Special Type of Series
(a) Numbers followed by their LCM or HCF.
For example: 1, 2, 3, 6, 4, 5, 12, 60, 5, 6, 7 ….
In the above series, every four numbers forms a block in which the fourth number is the LCM of first three numbers. Therefore, the number next to 7 is 210. i.e. LCM of 5, 6, 7 = 210
(b) Numbers followed by their product.
For example:
1, 2, 2, 4, 8, 32, ……
1×2=2;2×2=4;2×4=8;4×8=32;8×32=256,
Which is the next number in the series.
(c) By use of digit sum. For example: 12, 15, 21, 24, 30, ..
Next number = previous number + Digit-sum of previous number.
i.e., 15 = 12+(1+2)
21=15+(1+5)
24=21+(2+1)
30=24+(2+4)
∴ Next number = 30 +(3+0)= 33
Number Series Questions from Previous Year Exams
Quiz-summary
0 of 38 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
Information
Number Series Syllabus
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 38 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- Answered
- Review
-
Question 1 of 38
1. Question
1 points6 42 294 2058 14406?
Correct
Incorrect

-
Question 2 of 38
2. Question
1 points20 33 50 69 92 ?
Correct
Incorrect
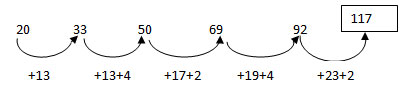
-
Question 3 of 38
3. Question
1 points13 20 14 19 15 ?
Correct
Incorrect
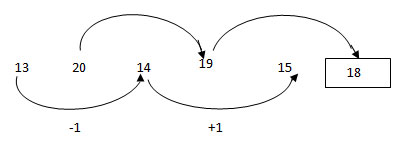
-
Question 4 of 38
4. Question
1 points9 27 36 63 99 ?
Correct
Incorrect
9+27= 36, 27+36= 63, 36+63=99,
?= 63+99=162
-
Question 5 of 38
5. Question
1 points7 26 63 124 215 ?
Correct
Incorrect
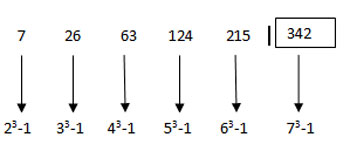
-
Question 6 of 38
6. Question
1 points3 19 115 691 ? 24883
Correct
Incorrect
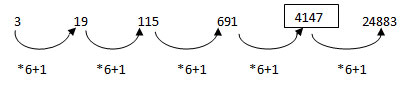
-
Question 7 of 38
7. Question
1 points5 10 20 ? 80 160
Correct
Incorrect
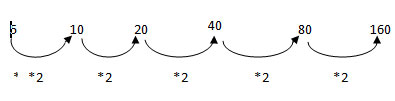
-
Question 8 of 38
8. Question
1 points10 11 14 19 26?
Correct
Incorrect
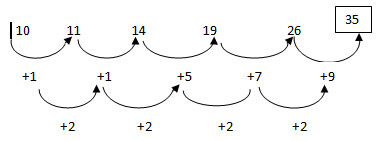
-
Question 9 of 38
9. Question
1 points1598 798 398 198 ? 48
Correct
Incorrect
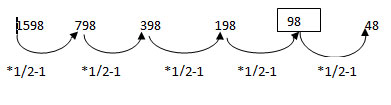
-
Question 10 of 38
10. Question
1 points5 10 15 20 25 ?
Correct
Incorrect
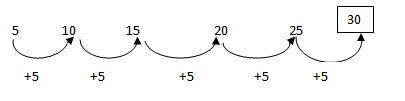
-
Question 11 of 38
11. Question
1 points5 13 25 41 ? 85 113
Correct
Incorrect
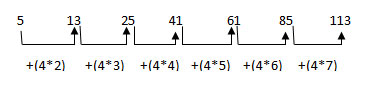
-
Question 12 of 38
12. Question
1 points16 24 36 54 81 121.5 ?
Correct
Incorrect
-
Question 13 of 38
13. Question
1 points15 16 14 17 13 18 ?
Correct
Incorrect
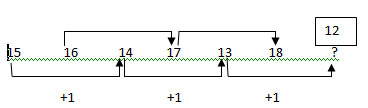
-
Question 14 of 38
14. Question
1 points22 23 27 36 52 77 ?
Correct
Incorrect
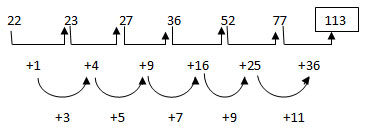
-
Question 15 of 38
15. Question
1 points4 2 3 7.5 ? 118.125
Correct
Incorrect
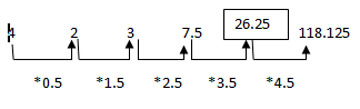
-
Question 16 of 38
16. Question
1 points1 5 17 53 161 485 ?
Correct
Incorrect
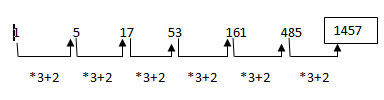
-
Question 17 of 38
17. Question
1 points15 50 155 470 1415 ?
Correct
Incorrect
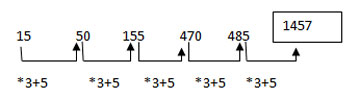
-
Question 18 of 38
18. Question
1 points888 888 444 148 ? 7.4
Correct
Incorrect
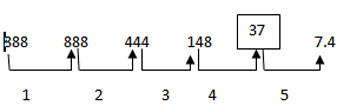
-
Question 19 of 38
19. Question
1 points11 13 19 26 35 46 59
Correct
Incorrect
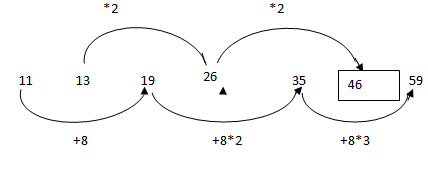
-
Question 20 of 38
20. Question
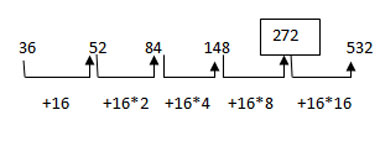
1 points36 52 84 148 272 532
Correct
Incorrect
-
Question 21 of 38
21. Question
1 points4, 7, 12, 19, 28, ?
Correct
Given solution is + 3, + 5, + 7, + 9, .....
So, missing term = 28 + 11 = 39.Incorrect
Given solution is + 3, + 5, + 7, + 9, .....
So, missing term = 28 + 11 = 39. -
Question 22 of 38
22. Question
1 points11, 13, 17, 19, 23, 25, ?
Correct
Given solution is + 2, + 4, + 2, + 4, .....
So, missing term = 25 + 4 = 29.Incorrect
Given solution is + 2, + 4, + 2, + 4, .....
So, missing term = 25 + 4 = 29. -
Question 23 of 38
23. Question
1 points2, 5, 9, ?, 20, 27
Correct
Given solution is + 3, + 4, + 5, + 6, .....
So, missing term = 9 + 5 = 14.Incorrect
Given solution is + 3, + 4, + 5, + 6, .....
So, missing term = 9 + 5 = 14. -
Question 24 of 38
24. Question
1 points4832, 5840, 6848, ?
Correct
Given solution is + 1008.
So, missing term = 6848 + 1008 = 7856.Incorrect
Given solution is + 1008.
So, missing term = 6848 + 1008 = 7856. -
Question 25 of 38
25. Question
1 points10, 100, 200, 310, ?
Correct
Given solution is + 90, + 100, + 110, .....
So, missing term = 310 + 120 = 430.Incorrect
Given solution is + 90, + 100, + 110, .....
So, missing term = 310 + 120 = 430. -
Question 26 of 38
26. Question
1 points28, 33, 31, 36, ?, 39
Correct
Given solution is + 5, – 2, + 5, – 2, .....
So, missing term = 36 – 2 = 34.Incorrect
Given solution is + 5, – 2, + 5, – 2, .....
So, missing term = 36 – 2 = 34. -
Question 27 of 38
27. Question
1 points125, 80, 45, 20, ?
Correct
Given solution is – 45, – 35, – 25, .....
So, missing term = 20 – 15 = 5.Incorrect
Given solution is – 45, – 35, – 25, .....
So, missing term = 20 – 15 = 5. -
Question 28 of 38
28. Question
1 points2, 15, 41, 80, ?
Correct
Given solution is + 13, + 26, + 39, .....
So, missing term = 80 + 52 = 132.Incorrect
Given solution is + 13, + 26, + 39, .....
So, missing term = 80 + 52 = 132. -
Question 29 of 38
29. Question
1 points6, 17, 39, 72, ?
Correct
Given solution is + 11, + 22, + 33, .....
So, missing term = 72 + 44 = 116.Incorrect
Given solution is + 11, + 22, + 33, .....
So, missing term = 72 + 44 = 116. -
Question 30 of 38
30. Question
1 points325, 259, 204, 160, 127, 105, ?
Correct
The given solution is – 66, – 55, – 44, – 33, – 22, .....
So, missing term = 105 – 11 = 94.Incorrect
The given solution is – 66, – 55, – 44, – 33, – 22, .....
So, missing term = 105 – 11 = 94. -
Question 31 of 38
31. Question
1 points0.5, 0.55, 0.65, 0.8, ?
Correct
The pattern is + 0.05, + 0.10, + 0.15, .....
So, missing term = 0.8 + 0.20 = 1.Incorrect
The pattern is + 0.05, + 0.10, + 0.15, .....
So, missing term = 0.8 + 0.20 = 1. -
Question 32 of 38
32. Question
1 points5, 6, 9, 15, ?, 40
Correct
The given solution is + 1, + 3, + 6, ..... i.e. + 1, + (1 + 2), + (1 + 2 + 3), .....
So, missing term = 15 + (1 + 2 + 3 + 4) = 25.Incorrect
The given solution is + 1, + 3, + 6, ..... i.e. + 1, + (1 + 2), + (1 + 2 + 3), .....
So, missing term = 15 + (1 + 2 + 3 + 4) = 25. -
Question 33 of 38
33. Question
1 points2, 3, 5, 7, 11, ?, 17
Correct
Clearly, the given series consists of prime numbers starting from 2. So, the missing term is the prime number after 11, which is 13.
Incorrect
Clearly, the given series consists of prime numbers starting from 2. So, the missing term is the prime number after 11, which is 13.
-
Question 34 of 38
34. Question
1 points4, 9, 25, ?, 121, 169, 289, 361
Correct
The given series consists of square of consecutive prime numbers i.e
So, missing term = 72 = 49.Incorrect
The given series consists of square of consecutive prime numbers i.e
So, missing term = 72 = 49. -
Question 35 of 38
35. Question
1 points4, 12, 36, 108, ?
Correct
The given solution is × 3.
So, missing term = 108 × 3 = 324.Incorrect
The given solution is × 3.
So, missing term = 108 × 3 = 324. -
Question 36 of 38
36. Question
1 points1, 2, 6, 7, 21, 22, 66, 67, ?
Correct
The pattern is + 1, × 3, + 1, × 3, + 1, × 3, + 1, .....
So, missing term = 67 × 3 = 201.Incorrect
The pattern is + 1, × 3, + 1, × 3, + 1, × 3, + 1, .....
So, missing term = 67 × 3 = 201. -
Question 37 of 38
37. Question
1 points1, 1, 2, 6, 24, ?, 720
Correct
The given solution is × 1, × 2, × 3, × 4, .....
So, missing term = 24 × 5 = 120.Incorrect
The given solution is × 1, × 2, × 3, × 4, .....
So, missing term = 24 × 5 = 120. -
Question 38 of 38
38. Question
1 points165, 195, 255, 285, 345, ?
Correct
Each number of the series is 15 multiplied by a prime number i.e. 15 × 11, 15 × 13, 15 × 17, 15 × 19, 15 × 23, .....
So, missing term = 15 × 29 = 435.Incorrect
Each number of the series is 15 multiplied by a prime number i.e. 15 × 11, 15 × 13, 15 × 17, 15 × 19, 15 × 23, .....
So, missing term = 15 × 29 = 435.
Number Series Video Lecture.
https://www.youtube.com/watch?v=pHm1qepw5Ro




Dear Sir / Mam,
My son preparing for Miltary Exam (AISSEE). Please give reasoning, Maths, Current Affairs, Intelligence, Language question papers with answer. Please sent to may mail : uarjun2015@gmail.com
send me pdf
Dear sir/madam,
will you please send - All type of competitive exam pdf’s reasoning general science gk questions papers arithmetic, verbal, Non verbal reasoning and comprehension with answers on my email.
Thank you
Send me pdf
Please send pdf to my akhilamarapu9390@gmail.com
Please sending my email ID reasonig
please send me mental ability coved all topics for competitive exam pdf plz
Excellent work sir
Plz kindly share All type of competitive exam pdf’s reasoning general science gk questions papers arithmetic, verbal,
Non verbal reasoning and comprehension with answers on my email vidhikhetarpal@gmail.com
Please send me pdf of all the bank exams related questions and their syllabus to my mail id yalamanchipranathi@gmail.com
Plz kindly send me any type of resoning trick at my imail id arabinda bag303@gmail.com
It can also be 121 because we can also take interval of prime number
Plz kindly share All type of competitive exam reasoning general science gk questions papers with amswer on my mail......
hiteshmeshram02@gmail.com
Send me reasoning, arthamatic,comprehension at my mail .. Saikarthikzpz@gmail.com
i like to study reasoning
lucknow
Send me reasoning arithmetic and comprehension at my email james2link@yahoo.com
Send me reasoning,arthamatic, comprehension at my email id princeshowkat786@gmail.com
sohanchopra213@gmail.com