Decision making for planning, policy, and management relies increasingly on quantitative reasoning, which entails the collection, analysis and interpretation of quantitative data. This course is designed to introduce principles and techniques to solve time and distance related problems.
Develop Logical Reasoning in a Problem-Solving Framework. One goal is to develop a disciplined logical analysis of “word” problems. Such reasoning is the foundation for building simple mathematical models of problems – models implicit in counting time and distance. A good way to learn this logical thinking is by working many exercises. Students will use this reasoning often (consciously or unconsciously) in computer science, operations research, and probability and statistics. However, a logical mind will serve a person well in ANY field.
At the end of these course students:
To be understood the types of formula are used to measure time and Distance.
To be able to calculate time and distance while an object that moves at a constant rate is said to be in uniform motion, Uniform motion problems may involve objects going the same direction, opposite directions, or round trips.
To be solving many problems related to time and distance and which can be useful to students to face interviews.
Prerequisities (Important Formulas):
Speed = Distance/Time
Time = Distance/speed
Distance = speed*time
1km/hr = 5/18 m/s
1 m/s = 18/5 Km/hr
If the ratio of the speed of A and B is a:b,then the ratio of the time taken by them to cover the same distance is 1/a : 1/b or b:a
Suppose a man covers a distance at x kmph and an equal distance at y kmph. then the average speed during the whole journey is (2xy/x+y) kmph
An object that moves at a constant rate is said to be in uniform motion. The formula d = rt gives the relationship between distance d, rater, and time t. Uniform motion problems may involve objects going the same direction, opposite directions, or round trips.
Time, Work and Distance Solved Examples
Example 1.) Walking at the rate of 4kmph a man cover certain distance in 2hr 45 min. Running at a speed of 16.5 kmph the man will cover the same distance in.
Answer: 40min Explanation: Distance = Speed * time
4*11/4 = 11km
New Speed = 16.5 kmph
Therefore time = D/S = 11/16.5 = 40min
Example 2.) A train covers a distance in 50 min, if it runs at a speed of 48kmph on an average. The speed at which the train must run to reduce the time of journey to 40min will be.
Answer: 60 min
Explanation: Time = 50/60 hr = 5/6hr
Speed = 48mph
distance = S*T = 48 * 5/6 = 40km
time = 40/60hr = 2/3hr
New speed = 40* 3/2 kmph = 60kmph
Example 3.) Two boys starting from the same place walk at a rate of 5kmph and 5.5kmph respectively. What time will they take to be 8.5km apart, if they walk in the same direction?
Answer: 17 hrs Explanation: The relative speed of
the boys = 5.5kmph – 5kmp = 0.5 kmph
Distance between them is 8.5 km
Time= 8.5km / 0.5 kmph = 17 hrs
Example 4.) In covering a distance of 30 km, Sachin takes 2 hours more than Rohit. If Sachin doubles his speed, then he would take 1 hour less than Rohit. Sachin speed is:
Answer: 5 kmph Explanation: Let Sachin’s speed be X km/hr.
Then, 30/x - 30/2x = 3
6x = 30
x = 5 km/hr.
Example 5.) A train 140m long running at 60kmph. In how much time will it pass a platform 260m long?
Work is the quantity of energy transferred from one system to another but for question based on this topic. OR Problem on work are based on the application of concept of ratio of time and speed.
Above mentioned definition of work throws light on three important points. 1.Work = 1 ( as it is always measured as a whole) = Distance 2.Rate at which work is done = speed 3.Number of days required to do the work = Time
Formulas:
1.Work from Days: If A can do a piece of work in n days, then A's 1 day's work =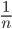 2.Days from Work: If A's 1 day's work =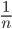 then A can finish the work in n days.
3.Ratio:
(a) If A is thrice as good a workman as B, then:
(b) Ratio of work done by A and B = 3 : 1.
(c) Ratio of times taken by A and B to finish a work = 1 : 3.
4.If A is 'x' times as good a workman as B, then he will take 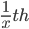of the time by B to do the same work.
5.A and B can do a piece of work in 'a' days and 'b' days respectively, then working together, they will take days to finish the work and in one day, they will finish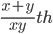 part of work
Problem 1: If 5 women or 8 girls can do a work in 84 days. In how many days can 10 women and 5 girls can do the same work?
Solution: Given that 5 women is equal to 8 girls to complete a work. So, 10 women = 16 girls. Therefore 10 women + 5 girls = 16 girls + 5 girls = 21 girls.
8 girls can do a work in 84 days then 21 girls can do a work in (8*) = 32 days.
Therefore 10 women and 5 girls can a work in 32 days
Problem 2: Worker A takes 8 hours to do a job. Worker B takes 10 hours to do the same job. How long it take both A & B, working together but independently,to do the same job?
Solution: A's one hour work = 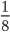. B's one hour work = 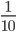. (A+B)'s one hour work
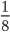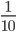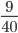= + =. Both A & B can finish the work in days
Problem 3: A can finish a work in 18 days and B can do the same work in half the time taken by A. Then, working together, what part of the same work they can finish in a day?
Solution: Given that B alone can complete the same work in days = half the time taken by A = 9 days
A's one day work =
B's one day work =
(A+B)'s one day work = + =
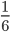
Problem 4: A is twice as good a workman as B and together they finish a piece of work in 18 days.In how many days will A alone finish the work.
Solution: if A takes x days to do a work then B takes 2x days to do the same work
= > + =
= > =
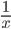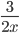= > x = 27 days.
Hence, A alone can finish the work in 27 days.
Problem 5: A can do a certain work in 12 days. B is 60% more efficient than A.
How many days does B alone take to do the same job?
Solution: Ratio of time taken by A & B = 160:100 = 8:5
Suppose B alone takes x days to do the job.
Then, 8:5::12:x
= > 8x = 5*12
= > x = days.
Time, Work and Distance Questions from Previous Year Exams
Time limit: 0
Quiz-summary
0 of 30 questions completed
Questions:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Information
IBPS bank clerk CWE
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 30 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
Average score
Your score
Categories
Not categorized0%
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Answered
Review
Question 1 of 30
1. Question
1 points
Nitesh goes to school from his village at the speed'of 4km/h and returns from school to village at the speed of 2 km/h. If he takes 6 h in all, then what is the distance between the village and the school?
Correct
Let the distance between the village.and school be x km.
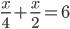
= 8 km
Incorrect
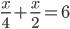
Let the distance between the village.and school be x km.
= 8 km
Question 2 of 30
2. Question
1 points
Five men can complete a piece of work in 24 days. In how many days will 12 men complete the same piece of work?.
Correct
Five men complete the work in = 24 days
.'. 1 man can complete the work in =
.'. 12 men will complete the work in =
= 10 days
Incorrect
Five men complete the work in = 24 days
.'. 1 man can complete the work in =
.'. 12 men will complete the work in =
= 10 days
Question 3 of 30
3. Question
1 points
A 175 m long train crosses a 35 m platform tn 12 s. What is the speed of the train in km/h?
Correct
Speed of train = m/s
km/hrs = 63km/hrs
Incorrect
Speed of train = m/s
km/hrs = 63km/hrs
Question 4 of 30
4. Question
1 points
A train running with the speed of 45 km/h crosses 300 m long another train running in the same direction. Find the speed of the second train.
Correct
Since, length of first train and time taken to cross are not given, therefore, the speed of the second train cannot be determined.
Incorrect
Since, length of first train and time taken to cross are not given, therefore, the speed of the second train cannot be determined.
Question 5 of 30
5. Question
1 points
If 3 men or 9 boys can finish a piece of work in 21 days. In how many days can 5 men and 6 boys together do the same piece of work?
Correct
Let the required number of days be x
3 Man = 9 boys
5 Man =
5 men and 6 boys =
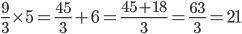
Boys = 21
21 : 9 :: 21 : x
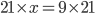
= 9 days
Incorrect
Let the required number of days be x
3 Man = 9 boys
5 Man =
5 men and 6 boys =
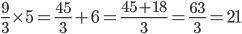
Boys = 21
21 : 9 :: 21 : x
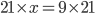
= 9 days
Question 6 of 30
6. Question
1 points
A and B together can do a piece of work in 4 days.If A alone can do it in 6 days, l.e. In how many days B can alone complete the same piece of work?
Correct
B's alone one day work =
.'. B can alone complete the work in 12 days.
Incorrect
B's alone one day work =
.'. B can alone complete the work in 12 days.
Question 7 of 30
7. Question
1 points
The average speed of a car is two-third average speed of a train which travels 270 km in 3 h. How much distance will the car cover in 5 h?
Correct
Average speed of train =
Average speed of car =
The distance =
Incorrect
Average speed of train =
Average speed of car =
The distance =
Question 8 of 30
8. Question
1 points
One pipe can fill a tank three times as fast as another pipe. If together the two pipes can fill the tank in 36 min, the slower pipe along wiltr be able to fill the tank in
Correct
Let the slower and fast pipe take x and min to fill the tank.
x = 144 min.
Incorrect
Let the slower and fast pipe take x and min to fill the tank.
x = 144 min.
Question 9 of 30
9. Question
1 points
Two cars A and B arerunning in the same direction. Car A had already covered a distance of 60 km when car B started running. The cars meet each other in 3 h after car B started running. What was the speed of car A?
Correct
Let the speed of cars A and B be x km/h and y km/h, respectively.
Thus, we cannot determine the speed of car A.
Incorrect
Let the speed of cars A and B be x km/h and y km/h, respectively.
Thus, we cannot determine the speed of car A.
Question 10 of 30
10. Question
1 points
A train runnin g at the speed of 72 km/h crosses a 260 m long platform in 23 s" What is the length of the train in metre?
Correct
Let the length of train be x m.
.'.
x= 200 m
Incorrect
Let the length of train be x m.
.'.
x= 200 m
Question 11 of 30
11. Question
1 points
A 300 m long train crosses a platform in 39 s while it crosses a slgnal pole in 18 s. What is the length of the platform?
Correct
Let the length of platform be x m.
Incorrect
Let the length of platform be x m.
Question 12 of 30
12. Question
1 points
A boat running downstream covers a distance of 16 km in 2 h while covering the same distance upstream it trake 4 h. What is the speed of the boat in still water?
Correct
.'. The Speed of boat in still water=
= 6 km/h.
Incorrect
.'. The Speed of boat in still water=
= 6 km/h.
Question 13 of 30
13. Question
1 points
A and B can do a work in 15 days, B and C in 20 days, C and A in 12 days. In how many days can they complete it, if they work together?
Correct
(A + B)'s one day work =
(B + C)'s one day work =
(C + A)'s one day work =
.'. (A + B +C)'s one day work =
=
Incorrect
(A + B)'s one day work =
(B + C)'s one day work =
(C + A)'s one day work =
.'. (A + B +C)'s one day work =
=
Question 14 of 30
14. Question
1 points
12 men complete a work in 9 days. After they have worked for 6 days, 6 more men join them' How many days will they take to complete the remaining work?
Correct
12 men complete a work in 9 days 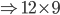= 108 man days
In 6 days, the 12 men have completed 72 man days
108 man days − 72 man days = 36 man days left
There are now 18 men
36 man days / 18 men = 2 days
It will take another 2 days to complete the work
Incorrect
12 men complete a work in 9 days 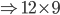= 108 man days
In 6 days, the 12 men have completed 72 man days
108 man days − 72 man days = 36 man days left
There are now 18 men
36 man days / 18 men = 2 days
It will take another 2 days to complete the work
Question 15 of 30
15. Question
1 points
Suresh can complete a job in 15 h. Ashutosh alone can complete the same job in fO h. If Suresh works alone for 9 h and then stops, in how many hours Ashutosh will complete the job alone?
Correct
Work done by Suresh in 9 h =
Remaining work=
Time take by Ashutosh to complete the work
= 4 h
Incorrect
Work done by Suresh in 9 h =
Remaining work=
Time take by Ashutosh to complete the work
= 4 h
Question 16 of 30
16. Question
1 points
A cistern can be filled up with water by a pipe in 5 h and it can be emptied by a second pipe in 4 h. If both the pipes are opened when the cistern is full, the time in which it will be emptied is
Correct
The tank emptied in 1 h
.'. The tank will be emptied in 20 h.
Incorrect
The tank emptied in 1 h
.'. The tank will be emptied in 20 h.
Question 17 of 30
17. Question
1 points
Two pipes can fiIt a tank in 12 h and 15 h respectively. A third pipe can empty it in 20 h. If the tank is empty and all the 3 pipes are opened, then the tank will be full in
Correct
When all the three pipes are opened together, the part of tank filled in 1 h
So, the tank will be filled completely in 10 h.
Incorrect
When all the three pipes are opened together, the part of tank filled in 1 h
So, the tank will be filled completely in 10 h.
Question 18 of 30
18. Question
1 points
A girl can do a job in 10 days, Her mother takes 25 days and her sister finishes it in 20 days. How long will they take to complete the job if they all together?
Correct
So all the three together will complete the work in 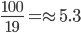days.
Incorrect
So all the three together will complete the work in 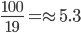days.
Question 19 of 30
19. Question
1 points
P is thrice as good a workman as Q and together they finish a piece of work in 24 days. The number of days taken by P alone to finish the work is:(po 2005)
Correct
P's 1 days' work) : (Q's 1 days' work) = 3 : 1
(P + Q)'s = 1 days work =
Hence, P alone can finish the work in 32 days.
Incorrect
P's 1 days' work) : (Q's 1 days' work) = 3 : 1
(P + Q)'s = 1 days work =
Hence, P alone can finish the work in 32 days.
Question 20 of 30
20. Question
1 points
Two workers P and Q working together completed a job in 4 days. If P worked twice as efficiently as he actually did and Q worked 1/2 as efficiently as he actually did, the work would have been completed in 4 days. P alone could complete the work in:
Correct
Let P's 1 day's work = x and Q's 1 day's work = y.
Then x + y = and
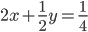
x =
∴ P's 1 day's work =
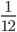
So, P alone could complete the work in = 12 days.
Incorrect
Let P's 1 day's work = x and Q's 1 day's work = y.
Then x + y = and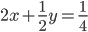
x =
∴ P's 1 day's work =
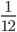
So, P alone could complete the work in = 12 days.
Question 21 of 30
21. Question
1 points
P can finish a work in 25 days and Q can do the same work in 20 days. Q worked for 8 days and left the job. In how many days, P alone can finish the remaining work?
Correct
Q's 8 days work =
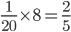
Remaining work =
work is done by P in 1 day.
work is done by P in 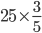= 15 day's
Incorrect
Q's 8 days work =
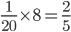
Remaining work =
work is done by P in 1 day.
work is done by P in 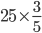= 15 day's
Question 22 of 30
22. Question
1 points
Seven men can complete a work in 12 days, they started the work and after 5 days, two men left. In how many days will the work be completed by the remaining men?
Correct
(7 × 12) men can complete the work in 1 day.
∴ 1 man's 1 day's work =
7 man's 5 days work =
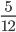
5 man's 1 days work =
work is done by them in
Incorrect
(7 × 12) men can complete the work in 1 day.
∴ 1 man's 1 day's work =
7 man's 5 days work =
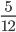
5 man's 1 days work =
work is done by them in
Question 23 of 30
23. Question
1 points
A, B and C together earn Rs. 300 per day, while A and C together earn Rs. 188 and B and C together earn Rs. 152. The daily earning of C is:
A sum of money is sufficient to pay A's wages for 21 days and B's wages for 28 days. The same money is sufficient to pay the wages of both for:(s b i 2006)
Correct
Let total money be Rs. x.
A's 1 day's wages =
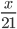
B's 1 day's wages = Rs
∴ (A + B)'s 1 day's wages =
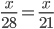
∴ Money is sufficient to pay the wages of both for 12 days.
Incorrect
Let total money be Rs. x.
A's 1 day's wages =
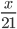
B's 1 day's wages = Rs
∴ (A + B)'s 1 day's wages =
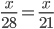
∴ Money is sufficient to pay the wages of both for 12 days.
Question 25 of 30
25. Question
1 points
10 men and 15 women together can complete a work in 6 days. It takes 100 days for one man alone to complete the same work. How many days will be required for one woman alone to complete the same work?
Correct
1 man's day's work = (10 men + 15 women)'s 1 day's work =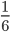
15 women's 1 day's work = =
∴ 1 woman alone can complete the work in 225 days.
Incorrect
1 man's day's work = (10 men + 15 women)'s 1 day's work =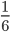
15 women's 1 day's work = =
∴ 1 woman alone can complete the work in 225 days.
Question 26 of 30
26. Question
1 points
A, B and C together can complete a piece of work in 10 days. All the three started working at it together and after 4 days A left. Then B and C together completed the work in 10 more days. A alone could complete the work in :
Correct
Work done by A, B and C in 4 days =
Remaining work =
(A + B + C)'s 1 day's work =
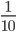
(B + C)'s 1 day's work =
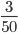
A's 1 day's work =
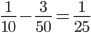
∴ A alone could complete the work in 25 days.
Incorrect
Work done by A, B and C in 4 days =
Remaining work =
(A + B + C)'s 1 day's work =
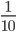
(B + C)'s 1 day's work =
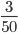
A's 1 day's work =
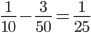
∴ A alone could complete the work in 25 days.
Question 27 of 30
27. Question
1 points
A takes twice time as much work as B in three-fourth of the time. If together they take 18 days to complete the work, how much time shall B take to do it?(ibps 2003)
Correct
Suppose B takes x days to do the work.
∴ A takes 2 days to do it.
(A + B)'s 1 day's work
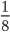
or x = 30
Incorrect
Suppose B takes x days to do the work.
∴ A takes 2 days to do it.
(A + B)'s 1 day's work
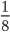
or x = 30
Question 28 of 30
28. Question
1 points
A man can do a piece of work in 5 days, but with the help of his son, he can do it in 3 days. In what time can the son do it alone?
Correct
(A + B)'s 1 day's work =
Work done by B in 23 days =
Remaining work =
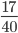work was done by (A + B) in 1 day
=9 day's
∴ A left after 9 days.
Incorrect
(A + B)'s 1 day's work =
Work done by B in 23 days =
Remaining work =
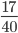work was done by (A + B) in 1 day
=9 day's
∴ A left after 9 days.
Question 29 of 30
29. Question
1 points
A, B and C can do a piece of work in 11 days, 20 days and 55 days respectively, working alone. How soon can the work be done if A is assisted by B and C on alternate days?
Correct
(A + B)'s 1 day's work =
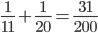
(A + C)'s 1 day's work =
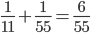
∴ Whole work will be done in (4 × 2) = 8 days.
Incorrect
(A + B)'s 1 day's work =
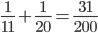
(A + C)'s 1 day's work =
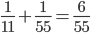
∴ Whole work will be done in (4 × 2) = 8 days.
Question 30 of 30
30. Question
1 points
If 12 men and 16 boys can do a piece of work in 5 days; 13 men and 24 boys can do it in 4 days, then the ratio of the daily work done by a man to that of a boy is
Correct
Let 1 man's 1 day's work = x and 1 boy's 1 day's work = y.
Then, 12x + 16y =
∴ Required ratio = x : y = = 2:1
Incorrect
Let 1 man's 1 day's work = x and 1 boy's 1 day's work = y.
of the time by B to do the same work.
days to finish the work and in one day, they will finish
part of work
) = 32 days.
. B's one hour work = 
. (A+B)'s one hour work
. Both A & B can finish the work in 
days
+
= 
= 
days.
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
min to fill the tank..gif)
.gif)
.gif)
.gif)
.gif)
.gif)
x= 200 m.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
0 Comments