This Module describes various standard geometrical structures that exist and methods/formulas or calculating its characteristic values that can be used for various applications/calculations. The structures include circle, triangle, cylinder etc., that exists within or as a shape, in all the practical entities we see in our daily life. So, calculating its area, Volume and perimeter gives the mathematical insight about the structure.
For example, in order to determine the number of tiles of specific shape to be placed over the floor of specific dimension, area of both tile and the floor become the basis.
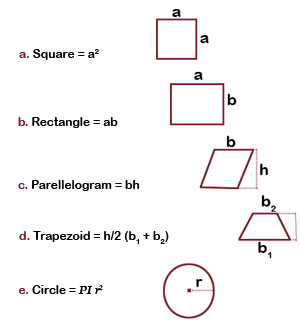
Prerequisites (Related Formulas) Area Calculations
Area is a quantity that expresses the extent of a two – dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat.
1 square kilometer = 1,000,000
square meters, 1 square meter = 10,000 square centimetres = 1,000,000 square millimetres
1 square centimetre = 100 square millimeters
1 square yard = 9 square feet
1 square mile = 3,097,600 square yards = 27,878,400 square feet
Volume is the quantity of three – dimensional space enclosed by some closed boundary, for example, the space that a substance (solid, liquid, gas, or plasma) or shape occupies or contains. Volume is often quantified numerically using the SI derived unit , the cubic metre.
1 litre = (10 cm)3 = 1000 cubic centimeters = 0.001 cubic metres,
1 cubic metre = 1000 liters.
Small amounts of liquid are often measured in millilitres,
Where 1millilitre = 0.001 litres = 1 cubic centimetre


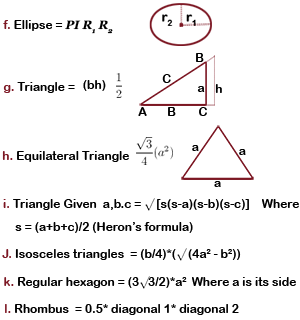
Surface Area Calculations
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve.
a. Surface Area of a Cube = 6a2  (a is the length of the side of each edge of the cube).
(a is the length of the side of each edge of the cube).
In words, the surface area of a cube is the area of the six squares that cover it. The area of one of them is a*a, or a2 . Since these are all the same, you can multiply one of them by six, so the surface area of a cube is 6 times one of the sides squared.
b. Surface Area of a Rectangular Prism = 2ab + 2bc + 2ac  (a, b, and c are the lengths of the 3 sides).
(a, b, and c are the lengths of the 3 sides).
In words, the surface area of a rectangular prism is the area of the six rectangles that cover it. But we don't have to figure out all six because we know that the top and bottom are the same, the front and back are the same, and the left and right sides are the same.
The area of the top and bottom (side lengths a and c) = a*c. Since there are two of them, you get 2ac. The front and back have side lengths of b and c. The area of one of them is b*c, and there are two of them, so the surface area of those two is 2bc. The left and right side have side lengths of a and b, so the surface area of one of them is a*b. Again, there are two of them, so their combined surface area is 2ab.
c. Surface Area of Any Prism  (b is the shape of the ends)
(b is the shape of the ends)
Surface Area = Lateral area + Area of two ends
(Lateral area) = (perimeter of shape b) * L
Surface Area = (perimeter of shape b) * L+ 2*(Area of shape b)
d. Surface Area of a Sphere = 4 pi r2 (r is radius of circle)
(r is radius of circle)
e. Surface Area of a Cylinder = 2 pi r2+ 2 pi r h  (h is the height of the cylinder, r is the radius of the top)
(h is the height of the cylinder, r is the radius of the top)
Surface Area = Areas of top and bottom +Area of the side
Surface Area = 2(Area of top) + (perimeter of top)* height
Surface Area = 2(pir2) + (2pir)* h
In words, the easiest way is to think of a can. The surface area is the areas of all the parts needed to cover the can. That's the top, the bottom, and the paper label that wraps around the middle. You can find the area of the top (or the bottom). That's the formula for area of a circle (pir2).
Since there is both a top and a bottom, that gets multiplied by two. The side is like the label of the can. If you peel it off and lay it flat it will be a rectangle. The area of a rectangle is the product of the two sides. One side is the height of the can, the other side is the perimeter of the circle, since the label wraps once around the can.
So the area of the rectangle is (2pir)* h. Add those two parts together and you have the formula for the surface area of a cylinder.
Perimeter Calculations
A perimeter is a path that surrounds an area. The word comes from the Greek peri (around) and meter (measure). The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape.

circle = pi d (where d is the diameter). The perimeter of a circle is more commonly known as the circumference.
Properties of various Geometrical structures
Triangle
In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°.
In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem.
In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles.
A right triangle (or right - angled triangle , formerly called a rectangled triangle) has one of its interior angles measuring 90° (a right angle). The side opposite to the right angle is the hypotenuse ; it is the longest side of the right triangle. The other two sides are called the legs of the triangle.
Right triangles obey the Pythagorean theorem : the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse: a2 +b2=c2, where a and b are the lengths of the legs and c is the length of the hypotenuse.
Triangles that do not have an angle that measures 90° are called oblique triangles.
A triangle that has all interior angles measuring less than 90° is an acute triangle or acute - angled triangle.
A triangle that has one angle that measures more than 90° is an obtuse triangle or obtuse - angled triangle.
A "triangle" with an interior angle of 180° (and collinear vertices) is degenerate.
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides (or 'edges') and four vertices or corners . Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon (5- sided), hexagon (6- sided) and so on. The Word quadrilateral is made of the words quad (meaning "four") and lateral (meaning "of sides").
The diagonals of parallelogram bisect each other
Each diagonal of a parallelogram divides it into two triangles of the same area
The diagonals of rectangle are equal and bisect each other
The diagonals of square are equal and bisect each other at right angles
The diagonals of rhombus are unequal and bisect each other at right angles
Circle
The circle is the shape with the largest area for a given length of perimeter.
A circle's circumference and radius are proportional.
The area enclosed and the square of its radius are proportional.
The constants of proportionality are 2 π and π, respectively.
The circle which is centered at the origin with radius 1 is called the unit circle.
Some Important Metrics
1. 10,000 sq meters = 1 hectare
2. 100 hectares = 1 sq kilo meter
3. 1000 millimeters = 1 meter
4. 100 centimeters = 1 meter
5. 1000 metres = 1 kilometer
6. 1000 kilograms = 1 mega gram or 1 tonne
7. 3.6 kilometers per hour = 1 meter per second
8. 3600 kilometers per hour = 1 kilometer per second
Volume Surface Area and Perimeter Questions from Previous Year Exams
Quiz-summary
0 of 29 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
Information
This test will cover Volume and Surface Area syllabus of Bank Clerk Exam.
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 29 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- Answered
- Review
-
Question 1 of 29
1. Question
1 pointsThe length of the longest pole that can be placed in a hall of dimensions 10 m x 8 m x 6 m, is
Correct
Incorrect
The length of the longest pole
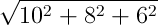
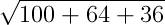
 =
= 
-
Question 2 of 29
2. Question
1 pointsThe length, breadth and height of a cuboid are increased by 10%, 20% and 25%, respectively. The percentage change in its volume is
Correct
Incorrect
Change in volume
 %
%Here x = 10, y = 20 and z = 25
therefor change in volume
=

=> (55 + 9.5 + 0.5)%= 65%
Since, the result is,positive, therefore the volume of cuboid is increased by 65%
-
Question 3 of 29
3. Question
1 pointsThe radius of a right circular cylinder is decreased by 10% but its height is increased by 15%. What is the percentage change in its volume?
Correct
Incorrect
Here, x = -10, Y = -10 and z = 15
Therefor change in volume
=

=
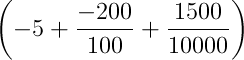
-5 -2 + 0.15 %
= -6.85 %
Since, result is negative" therefore the volume of the cylinder is decreased by 6.85%.
-
Question 4 of 29
4. Question
1 pointsIf whole surface area of a sphere is
.gif) , then its radius will beCorrect
, then its radius will beCorrect

=>

=> r = 5
Therefor Radius of the Sphere = 5
Incorrect

=>

=> r = 5
Therefor Radius of the Sphere = 5
-
Question 5 of 29
5. Question
1 pointsIf the volumes of two cones are in the ratio 1:4 and their diameter are in the ratio 4 : 5, then the ratio of their heights is
Correct
Given,
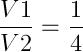
and

therefor

=>

=>

=>

=>

=>

=>
 Incorrect
Incorrect
Given,
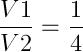
and

therefor

=>

=>

=>

=>

=>

=>

-
Question 6 of 29
6. Question
1 pointsA hemispherical bowl of internal radius g cm contains a liquid. This liquid is filled into cylindrical shaped small bottles of diameter B cm and height 4 cm. How many bottles will be needed to empty the bowl?
Correct
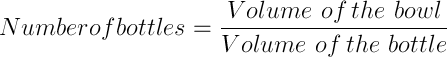
.gif)
.gif) Incorrect
Incorrect
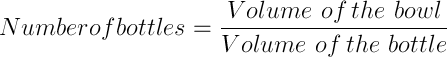
.gif)
.gif)
-
Question 7 of 29
7. Question
1 pointsIf the surface area of cube is 486 cm2, then its volume will be
Correct
Incorrect
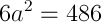
=>

=> a = 9
therefor Volume =
-
Question 8 of 29
8. Question
1 pointsIf the diagonal of a cubical box is , then its surface area will be
Correct
Incorrect

.gif)

a = 10 cm
therefor surface area of the cube
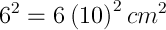
=
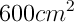
-
Question 9 of 29
9. Question
1 pointsThree cubes whose edges are 8 cm, 6 cm and 1 cm respectively are melted without any loss of metal into a single cube. The surface area of the new cube is
Correct
Incorrect
Volume of the new cube =


=>

=>

Therefor surface area of a new cube =

= 6 X 81
= 486
-
Question 10 of 29
10. Question
1 pointsA hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of cone is
Correct
Incorrect
According to the question,
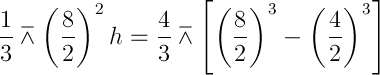


h= 14cm
-
Question 11 of 29
11. Question
1 pointsThe dimensions of a brick are 20 cm x 10 cm. How many bricks will be required. to construct a wall 4g0 m long, 100 cm wide and 600 cm high?
Correct
Incorrect
.gif)

= 2880000
-
Question 12 of 29
12. Question
1 pointsA cylindrical tube is open at both ends. Its external and internal radii are 15 cm and LZ cm, respectively. If the length of the tube is 35 cm, the volume of the material of the tube will be
Correct
Incorrect
Volume of the material =

=

= 8910

-
Question 13 of 29
13. Question
1 pointsA stream of water flows out of a rectangular opening 3 m x 2 m with speed 1.5 km/h. How much water passes through the opening in 5 min?
Correct
Incorrect
Speed of water = 1.5 km/h
=

Time = 5min = 300s
therefor Volume of water = area of the opening x speed of water x time
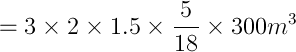
=

-
Question 14 of 29
14. Question
1 pointsIn a triangle, two sides of 12cm and 5 cm are at right angle. If the triangle is revolved along 12 cm side the curved surface area of the cone, so formed will be
Correct
Incorrect
Height of cone so formed = 12 cm
Radius of cone so formed = 5 cm
Therefor Curved surface area =
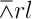


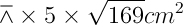

-
Question 15 of 29
15. Question
1 pointsA rectangular wooden box of thickness 10 cm measures externally 220 cm in length, 170 cm in breadth and 120 cm in height. The volume of the wood required to make it is
Correct
Internal dimensions of the wooden box
.gif)
.gif)
.'. Vo1ume of the wood
.gif)
.gif)
.gif) Incorrect
Incorrect
Internal dimensions of the wooden box
.gif)
.gif)
.'. Vo1ume of the wood
.gif)
.gif)
.gif)
-
Question 16 of 29
16. Question
1 pointsThree solid of cubes of sides 1 cm , 6 cm and 8 cm are melted to form a new cube. Find the surface area of the cube s formed.
Correct
Volume of new cube =
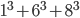 =729
=729
Edge of new cube =
![\sqrt[3]{729}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_dcc836570b9636c61de133aa8d9a2285.gif) =9
=9∴ Surface area of the new cube = (6 × 9 × 9) ⇒ 486
Incorrect
Volume of new cube =
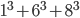 =729
=729
Edge of new cube =
![\sqrt[3]{729}](https://questionpaper.org/wp-content/plugins/latex/cache/tex_dcc836570b9636c61de133aa8d9a2285.gif) =9
=9∴ Surface area of the new cube = (6 × 9 × 9) ⇒ 486
-
Question 17 of 29
17. Question
1 pointsHow many copper rods, each of length 7m and diameter 2 cm can be made out of 0.88 cubic metre of copper.
Correct
Incorrect
-
Question 18 of 29
18. Question
1 pointsA iron sphere of diameter 18 cm is drawn into a wire of diameter 4 mm. Find the length of the wire.(sbi 2005)
Correct
Volume of sphere =
 =927
=927Volume of wire = (π × 0.2 × 0.2 × h)
∴ 972π =

⇒ h = (972 × 5 × 5)cm =
 =243 mIncorrect
=243 mIncorrect
Volume of sphere =
 =927
=927Volume of wire = (π × 0.2 × 0.2 × h)
∴ 972π =

⇒ h = (972 × 5 × 5)cm =
 =243 m
=243 m -
Question 19 of 29
19. Question
1 pointsFind the surface area of a sphere of radius 17.5 cm.
Correct
Surface area =
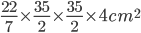 =3850Incorrect
=3850Incorrect
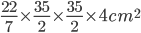 =3850
=3850 -
Question 20 of 29
20. Question
1 pointsFind the length of the longest perch that can be placed in a hall 12 m long, 8 m broad and 9m high.
Correct
Length of the longest perch = Length of the diagonal of the hall
 =
= =17 mIncorrect
=17 mIncorrect
Length of the longest perch = Length of the diagonal of the hall
 =
= =17 m
=17 m -
Question 21 of 29
21. Question
1 pointsThe diagonal of a cube is 6\sqrt{3} cm. Find its volume and surface area.
Correct
Let the edge of the cube be a. Then,
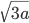 =6
=6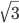 ⇒ a = 6.
⇒ a = 6.So, Volume = ⇒ 216

(6 × 6 × 6)= 216
 Incorrect
Incorrect
Let the edge of the cube be a. Then,
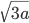 =6
=6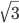 ⇒ a = 6.
⇒ a = 6.So, Volume = ⇒ 216

(6 × 6 × 6)= 216

-
Question 22 of 29
22. Question
1 pointsFind the length of canvas 1.25 m wide required to build a conical camp of base radius 7 meters and height 24 meters.
Correct
Here, r = 7 m and h = 24 m.
So, l =
 =
= =25 m
=25 mArea of canvas = πrl ⇒
 =
=
Length of canvas =
 =
= =440 mIncorrect
=440 mIncorrect
Here, r = 7 m and h = 24 m.
So, l =
 =
= =25 m
=25 mArea of canvas = πrl ⇒
 =
=
Length of canvas =
 =
= =440 m
=440 m -
Question 23 of 29
23. Question
1 pointsThe radii of the bases of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. Find the ratio of their volumes.
Correct
Let the radii of the and cone be 3r and 4r and their heights be 2h and 3h respectively.
∴
 =
=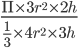 =
=
= 9:8
Incorrect
Let the radii of the and cone be 3r and 4r and their heights be 2h and 3h respectively.
∴
 =
=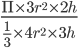 =
=
= 9:8
-
Question 24 of 29
24. Question
1 pointsWater flows into a tank 200m × 150 m through a rectangular pipe 1.5m × 1.25 m @ 20 kmph. In what time (in minutes) will the water rise by 2 meters ?
Correct
Volume required in the tank (200 × 150 × 2)
Length of the water column flown in 1 min. =
 =
=
Volume flown per minute =
 =625
=625∴ Required time =

⇒ 96 min.
Incorrect
Volume required in the tank (200 × 150 × 2)
Length of the water column flown in 1 min. =
 =
=
Volume flown per minute =
 =625
=625∴ Required time =

⇒ 96 min.
-
Question 25 of 29
25. Question
1 pointsA rectangular block 6 cm by 12 cm by 15 cm is cut up in to an exact number of equal cubes. Find the least possible number of cubes
Correct
volume of the block = (6 × 12 × 15) = 1080
Side of the largest cube = H.C.F. of 6 cm, 12 cm, 15 cm = 3 cm.
Volume of this cube = (3 × 3 × 3) = 27
∴ Number of cubes =
 =40Incorrect
=40Incorrect
volume of the block = (6 × 12 × 15) = 1080
Side of the largest cube = H.C.F. of 6 cm, 12 cm, 15 cm = 3 cm.
Volume of this cube = (3 × 3 × 3) = 27
∴ Number of cubes =
 =40
=40 -
Question 26 of 29
26. Question
1 pointsA cone and a sphere have equal radii and equal volumes. Find the ratio of the diameter of the sphere to the height of the cone.
Correct
Let radius of each be R and height of the cone be H.

or
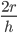 =
= 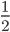
or
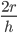 =
= 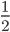
Required ratio = 1: 2Incorrect
Let radius of each be R and height of the cone be H.

or
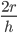 =
= 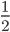
or
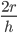 =
= 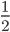
Required ratio = 1: 2 -
Question 27 of 29
27. Question
1 pointsA cone, a hemisphere and a cylinder stand on equal bases and have the same height. Find the ratio of thier volumes.
Correct
Let R be the radius of each.
Height of hemis[here = Its radius = R.
∴ Height of each = R .
Ratio of volumes =
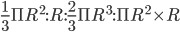
= 1 : 2 : 3
Incorrect
Let R be the radius of each.
Height of hemis[here = Its radius = R.
∴ Height of each = R .
Ratio of volumes =

= 1 : 2 : 3 -
Question 28 of 29
28. Question
1 pointsFind the number of lead balls, 1 each 1 cm in the diameter that can be made from a sphere of diameter 12 cm.
Correct
Volume of larger sphere =
 =
=
Volume of 1 small lead ball =

Number of lead balls = 1728
Incorrect
Volume of larger sphere =
 =
=
Volume of 1 small lead ball =

Number of lead balls = 1728
-
Question 29 of 29
29. Question
1 pointsThe dimensions of an open box are 50 cm, 40 cm and 23 cm. Its thickness is 3 cm. If cubic cm of metal used in the box weighs 0.5 gms, Find the weight of the box.
Correct
Volume of the metal used in the box = External Volume - Internal Volume
= [( 50 × 40 × 23) - (44 × 34 × 20)]=1680
Weight of the metal =
 =8.04 kgIncorrect
=8.04 kgIncorrect
Volume of the metal used in the box = External Volume - Internal Volume
= [( 50 × 40 × 23) - (44 × 34 × 20)]=1680
Weight of the metal =
 =8.04 kg
=8.04 kg
Volume Surface Area and Perimeter Video Lecture




0 Comments