Some Basic Concept of Vector: Let l be any straight line in plane or three dimensional space. This line can be given two directions by means of arrowheads. A line with one of these directions prescribed is called a directed line {Fig 10.1 (i), (ii)}. Now observe that if we restrict the line l to the line segment AB, then a magnitude is prescribed on the line l with one of the two directions, so that we obtain a directed line segment {Fig 10.1(iii)}. Thus, a directed line segment has magnitude as well as direction.
 Definition: A quantity that has magnitude as well as direction is called a vector .
Definition: A quantity that has magnitude as well as direction is called a vector .
Notice: That a directed line segment is a vector fig {10.1(iii)}, denoted by as
or simply as
, and read a ‘ vector
’ or ‘vector
’.
The point A from where the vector  ’ starts is called its initial point , and the point B where it ends is called its terminal point. The distance between initial and terminal points of a vector is called the magnitude (or length) of the vector, denoted as
’ starts is called its initial point , and the point B where it ends is called its terminal point. The distance between initial and terminal points of a vector is called the magnitude (or length) of the vector, denoted as  , or a .The arrow indicates the direction of the vector.
, or a .The arrow indicates the direction of the vector.
Position Vector
A vector  simply means the displacement from a point A to the point B. Now consider a situation that a girl moves from A to B and then from B to C (Fig 10.7). The net displacement made by the girl from point A to the point C, is given by the vector
simply means the displacement from a point A to the point B. Now consider a situation that a girl moves from A to B and then from B to C (Fig 10.7). The net displacement made by the girl from point A to the point C, is given by the vector  and express
and express 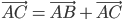
This is known as the triangle law of vector addition.
If we have two vectors  by the two adjacent sides of a parallelogram in magnitude and direction (Fig 10.9), then their sum is represented in magnitude and direction by the diagonal of the parallelogram through their common point. This is known as the parallelogram law of vector addition.
by the two adjacent sides of a parallelogram in magnitude and direction (Fig 10.9), then their sum is represented in magnitude and direction by the diagonal of the parallelogram through their common point. This is known as the parallelogram law of vector addition.
Using triangle law , 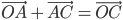
 (since
(since 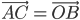

Which is parallelogram law. Thus, we may say that the two laws of vector addition are equivalent to each other
Properties of Vector Addition
1) For any two vector 
 (commutative properties)
(commutative properties)
2) For any three properties 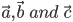
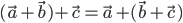 (Associative properties )
(Associative properties )
Note: The associative property of vector addition enables us to write the sum of three vectors
as without using brackets. Note that for any vector
, we have
Here , the zero vector is called additive identity for the vector addition .
Multiplication of a Vector by a Scalar
Let be a given vector and λ a scalar. Then the product of the vector a by the scalar λ , denoted as  , is called the multiplication of vector
, is called the multiplication of vector  , by the scalar λ. Note that ,
, by the scalar λ. Note that ,  , is also a vector, collinear to the vector
, is also a vector, collinear to the vector  , . The vector
, . The vector  , has the direction same (or opposite) to that of vector
, has the direction same (or opposite) to that of vector  , according as the value of λ is positive (or negative).Also, the magnitude of vector
, according as the value of λ is positive (or negative).Also, the magnitude of vector  , Is |λ| times the magnitude of the vector
, Is |λ| times the magnitude of the vector  , i.e ,
, i.e , 
A geometric visualisation of multiplication of a vector by a scalar is given in( Fig 10.12)
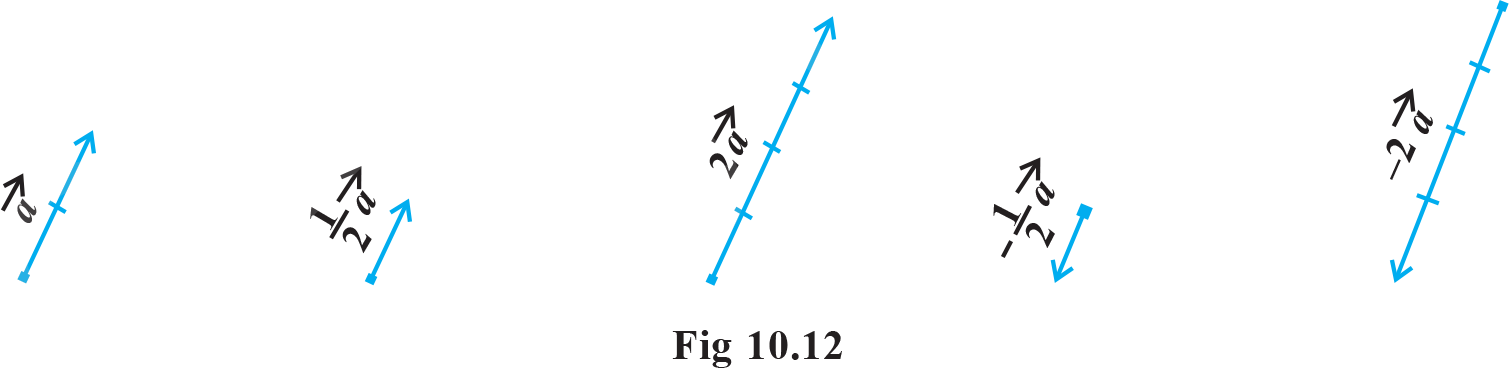
When  which is a vector having magnitude equal to the magnitude of
which is a vector having magnitude equal to the magnitude of  the vector
the vector  is called negative vector .(or additive inverse ) of vector a
is called negative vector .(or additive inverse ) of vector a  and we always have .
and we always have .
 . Also , if
. Also , if  , provide 0 , i.e
, provide 0 , i.e  is not a null vector , then
is not a null vector , then  represents the unit vector in the direction of. We write it as
represents the unit vector in the direction of. We write it as 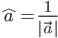
Note:
- One may observe that whatever be the value of λ , the vector
 is always collinear to the vector
is always collinear to the vector  . In fact, two vectors
. In fact, two vectors  are collinear if and only if there exists a nonzero scalar λ such that
are collinear if and only if there exists a nonzero scalar λ such that 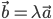 . If the vectors
. If the vectors  are given in component form , i.e ,
are given in component form , i.e , 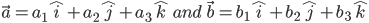
- If two vectors are collinear if and only if
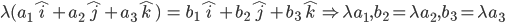

- If
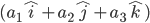 ,this is called the direction of ratio
,this is called the direction of ratio 
- In case if it is given that l ,m ,n are direction cosine of a vector , then
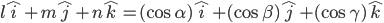 is the unit vector in the direction of that vector, where α , β and γ are the angles which the vector makes with x , y and z axes respectively .
is the unit vector in the direction of that vector, where α , β and γ are the angles which the vector makes with x , y and z axes respectively .
Example: find the unit vector in the direction of vector 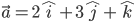
Solution: The unit vector in the direction of a vector  is given by
is given by 
Now 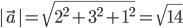
Therefore 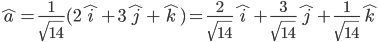
Example: Find the unit vector in the direction of the sum of the vector 
Solution: The sum of the given vector 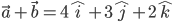 , Let
, Let 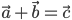
 , Thus the require unit vector is
, Thus the require unit vector is

Components of a Vector
Let us take the points A(1, 0, 0), B(0, 1, 0) and C(0, 0, 1) on the x -axis, y -axis and z -axis, respectively. Then, clearly .
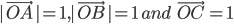

The vector 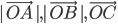 each having magnitude 1,are called unit vectors along the axes OX, OY and OZ respectively and denoted by
each having magnitude 1,are called unit vectors along the axes OX, OY and OZ respectively and denoted by  respectively (Fig 10.13).
respectively (Fig 10.13).
Now, consider the position vector OP of a point P (x , y, z) as in Fig 10.14. Let P1 be the foot of the perpendicular from P on the plane XOY. We, thus, see that P1 P is parallel to z – axis.
Therefore it follows that 

The length of any vector = , is readily determined by applying the Pythagoras theorem twice. We note that in the right angle triangle OQP1. (Fig 10.14) 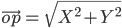

Vector joining two point :  are any two points
are any two points  with the origin O, and applying triangle law , from the triangle
with the origin O, and applying triangle law , from the triangle  ,we have
,we have

Section Formula
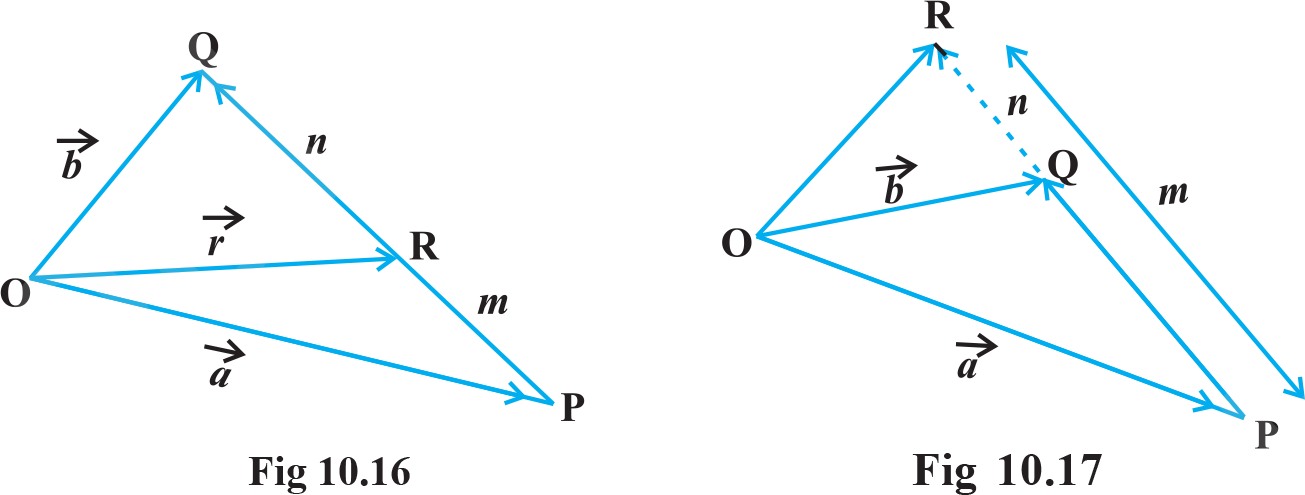
Let P and Q be two points represented by the position vectors OP and OQ , respectively, with respect to the origin O. Then the line segment joining the points P and Q may be divided by a third point, say R, in two ways – internally (Fig 10.16) and externally (Fig 10.17). Here, we intend to find the position vector OR for the point R with respect to the origin O .we take the two cases ;
Case I) where R divided PQ internally . where m and n point R divides PQ internally in the ratio of m : n . Now from triangles ORQ and OPR, we have,

Hence , the position vector of the point R which divides P and Q internally in the ratio of m: n is given b 
 Case II) When R divides PQ externally (Fig 10.17). We leave it to the reader as an exercise to verify
Case II) When R divides PQ externally (Fig 10.17). We leave it to the reader as an exercise to verify
that the position vector of the point R which divides the line segment PQ externally in the ratio m : n , i.e
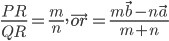
Product of two vector : other algebraic operation which we intend to discuss regarding vectors is their product. We may recall that product of two numbers is a number, product of two matrices is again a matrix. But in case of functions, we may multiply them in two ways, namely, multiplication of two functions point wise and composition of two functions. Similarly, multiplication of two vectors is also defined in two ways, namely, scalar (or dot) product where the result is a scalar, and vector (or cross) product where the result is a vector. Based upon these two types of products for vectors, they have found various applications in geometry, mechanics and engineering. In this section, we will discuss these two types of products.
Scalar (or dot ) product of two vector :The scalar product of of two non zero vector a and vector b , denoted by vector 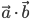 is define as
is define as 
where, θ is the angle between and 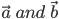 , 0 is not defined, and in this case
, 0 is not defined, and in this case
Observation
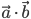 is real number
is real number- Let
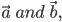 be two nonzero vector , then
be two nonzero vector , then 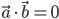 if and only if
if and only if 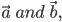 are perpendicular to each other i.e
are perpendicular to each other i.e 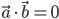 ,
, - If θ = 0, then ,
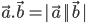 in particular
in particular 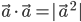 as θ in this case is 0.
as θ in this case is 0. - If θ = π , then
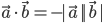 in particular
in particular 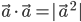 as θ in this case is
as θ in this case is 
- In view of the Observations 2 and 3, for mutually perpendicular unit vector
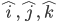 we have ,
we have , 
- The angle between two non zero vector
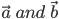 is given by
is given by 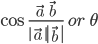

- The scalar product is commutative i.e

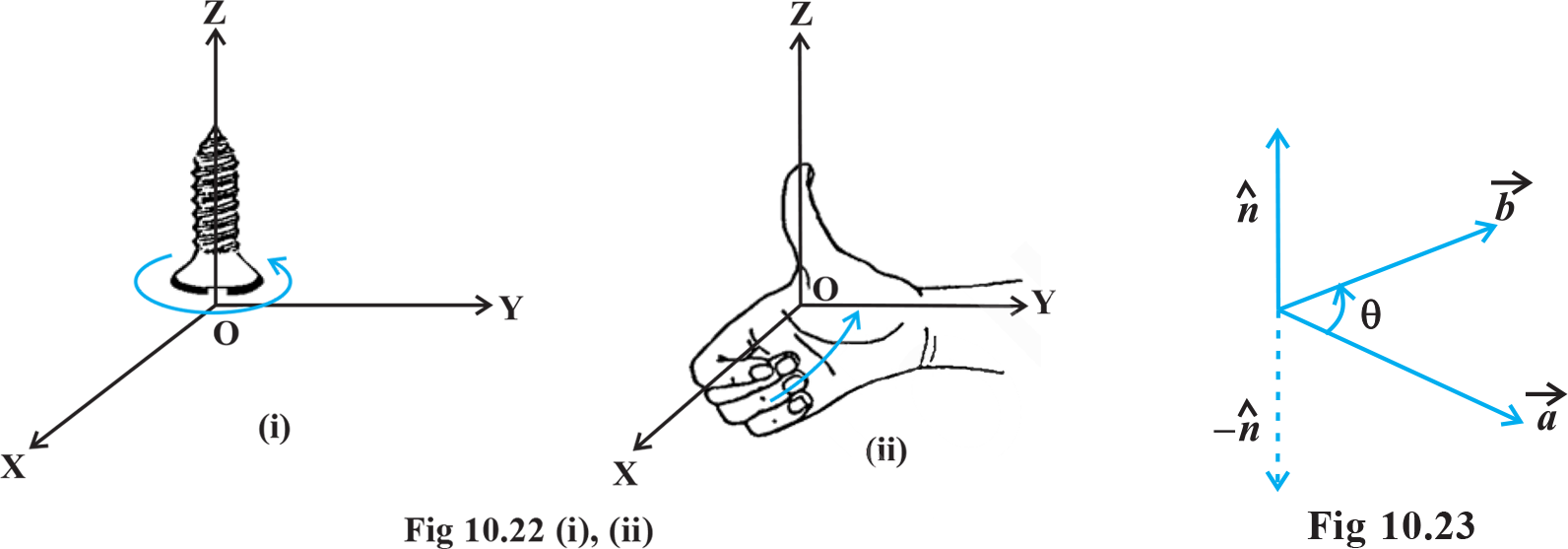
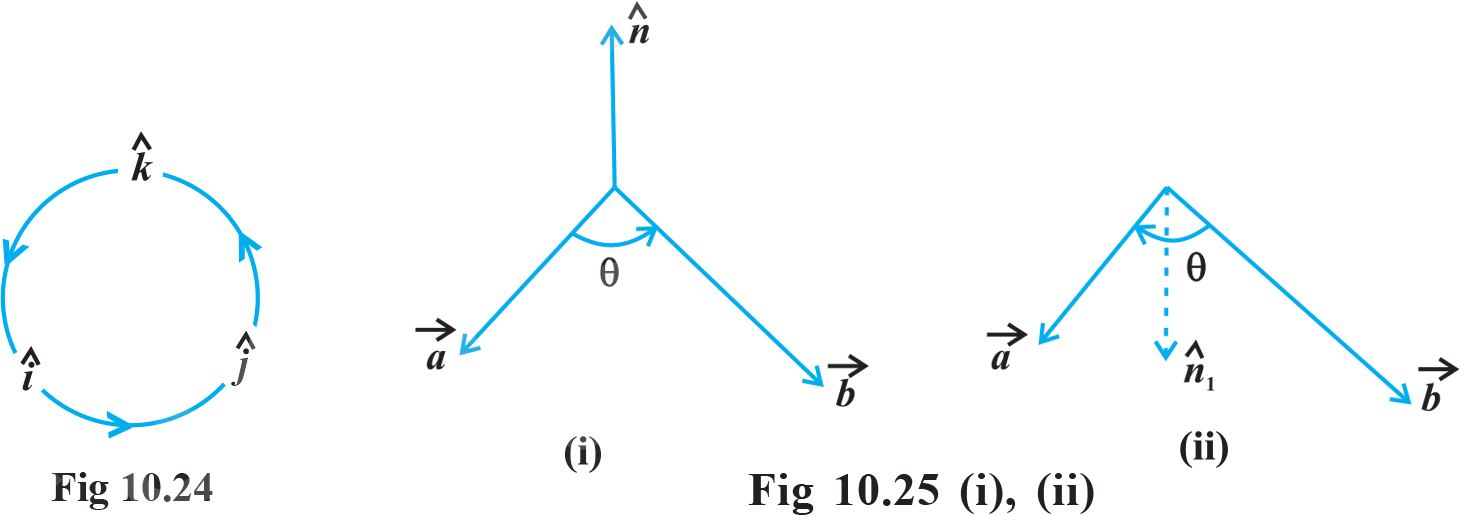
- Cross product of two vector : he three dimensional right handed rectangular coordinate system. In this system, when the positive x -axis is rotated counter clockwise nto the positive y -axis, a right handed (standard) screw would advance in the direction of the positive z -axis (Fig 10.22(i)). In a right handed coordinate system, the thumb of the right hand points in the direction of the positive z -axis when the fingers are curled in the direction away from the positive x-axis toward the positive y -axis (Fig 10.22(ii).
Definition
The vector product of two nonzero vectors  , is denoted by
, is denoted by  where, θ is the angle between
where, θ is the angle between 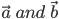 and ≤θ≤π and
and ≤θ≤π and  is a unit vector perpendicular to both
is a unit vector perpendicular to both 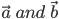 , such that ,
, such that , 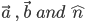 and form a right handed system (Fig 10.23). i.e., the right handed system rotated from
and form a right handed system (Fig 10.23). i.e., the right handed system rotated from 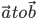 moves in the direction of . If either , then θ is not defined and in this case, we define of
moves in the direction of . If either , then θ is not defined and in this case, we define of 
Observation
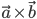 is a vector
is a vector- Let
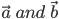 be two nonzero vector ,Then
be two nonzero vector ,Then  if and only if
if and only if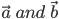 are parallel (or collinear) to each other . in particular
are parallel (or collinear) to each other . in particular 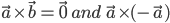 , since in the first situation, θ = 0 and in the second one, θ = π , making the value of sinθ to be 0
, since in the first situation, θ = 0 and in the second one, θ = π , making the value of sinθ to be 0 - In view of the Observations 2 and 3, for mutually perpendicular
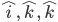 (fig 10.24)
(fig 10.24) - we have ,
 unit vector
unit vector 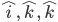

- In terms of vector product, the angle between two vectors and may be given as
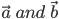
- It is always true that the vector product is not commutative, as
 Indeed, , where
Indeed, , where  form a right handed system, i.e., θ is traversed from .
form a right handed system, i.e., θ is traversed from .  is a vector Fig 10.25 (i). While,
is a vector Fig 10.25 (i). While,  ,where,
,where, 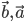 ,and
,and 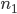 form a right handed system i.e. θ is traversed from .
form a right handed system i.e. θ is traversed from .
Points to Remember
- position vector of a point p(x,y,z) is given as
 , and it’s magnitude by
, and it’s magnitude by 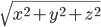
- The scalar components of a vector are its direction ratios, and represent its projections along the respective axes.
- The magnitude (r ), direction ratios (a , b, c) and direction cosines (l, m, n) of any vector are related as

- Th e vector sum of the three sides of a triangle taken in order is 0
- The vector sum of two coinitial vectors is given by the diagonal of the parallelogram whose adjacent sides are the given vectors.
- The multiplication of a given vector by a scalar λ , changes the magnitude of the vector by the multiple |λ|, and keeps the direction same (or makes it opposite) according as the value of λ is positive (or negative).
- For a given a , the vector
 gives the unit vector in the direction of vector a.
gives the unit vector in the direction of vector a. - The position vector of a point R dividing a line segment joining the points P and Q whose position vectors are
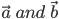 respectively in the ratio m: nInternally is given by :
respectively in the ratio m: nInternally is given by : 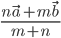 Externally , is given by :
Externally , is given by : 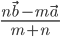
- The scalar product of two given vector
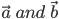 having angle θ between them is define as \vec{a}\cdot
having angle θ between them is define as \vec{a}\cdot 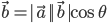 Also when
Also when 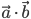 is given the angle , θ between the vector
is given the angle , θ between the vector 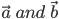 may be determine by
may be determine by 
- If θ is the angle between two vectors
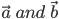 , then their cross product is given as
, then their cross product is given as , where unit vector
, where unit vector  , perpendicular to the plane containing
, perpendicular to the plane containing 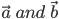 . Such that
. Such that  . form right handed system of coordinate axes.
. form right handed system of coordinate axes.
Vector Important Video Lecture

0 Comments