Plan figures
| Figures | Perimeter | Area | Image |
| Triangle | = a + b + c | 
Where s =
|
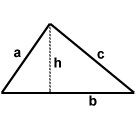 |
| Right angled triangle | 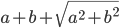 |
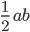 |
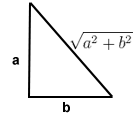 |
| Equilateral triangle | 3a | 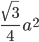 |
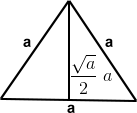 |
| Isosceles triangle | 2a + b | 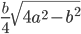 |
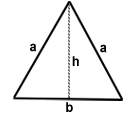 |
| Circle | 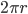 |
 |
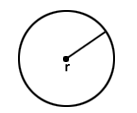 |
| Sector of a circle | 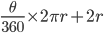 ( ( is in degrees) is in degrees) |
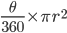 |
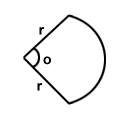 |
| Square | 4a |  |
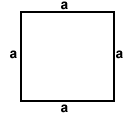 |
| Rectangle | 2(l + b) | lb | 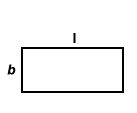 |
| Trapezium | a + b + c + d | 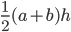 |
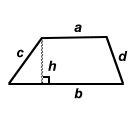 |
| Parallelogram | 2(a + b) | bh or ab 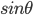 |
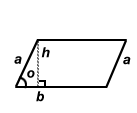 |
| Cyclic quadrilateral | a + b + c + d | 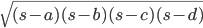
S = |
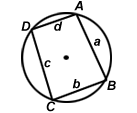 |
| Rhombus | 4a | 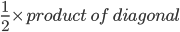 |
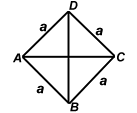 |
| Ring |  |
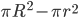 |
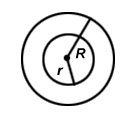 |
Solids
| Figure | Lateral Surface Area | Total Surface Area | Volume | Images |
| Cube | 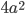 |
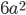 |
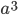 |
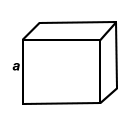 |
| Cuboid | 2h(l + b) | 2(lb + bh + lh) | lbh | 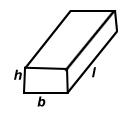 |
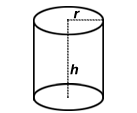
| Cylinder | 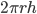 |
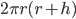 |
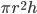 |
 |
| Cone | 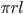 |
 |
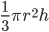 |
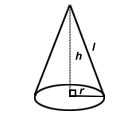 |
| Sphere | 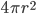 |
 |
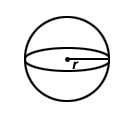 |
|
| Hemisphere | 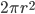 |
 |
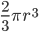 |
 |
Important Questions for Mensuration
Quiz-summary
0 of 50 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
Information
Mensuration
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 50 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Answered
- Review
-
Question 1 of 50
1. Question
1 pointsThe number of revolutions made by a bicycle wheel 56 cm in diameter in covering a distance of 1.1 km is
Correct
Number of revolutions =

Circumstance of wheel =
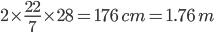
No. of revolutions =
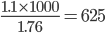 Incorrect
Incorrect
Number of revolutions =

Circumstance of wheel =
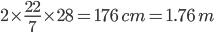
No. of revolutions =
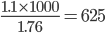
-
Question 2 of 50
2. Question
1 pointsThe area of a circular field is 13.86 hectare. The cost of fencing it @ Rs. 0.60/m is
Correct
A =
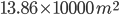
=

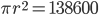

R = 210
Length of fence =
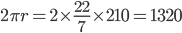
Cost =
 Incorrect
Incorrect
A =
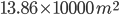
=

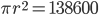

R = 210
Length of fence =
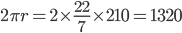
Cost =

-
Question 3 of 50
3. Question
1 pointsThe base of an isosceles triangle is 8 cm and its perimeter is 18 cm. The area of triangle is
Correct
a + a + 8 = 18
 a = 5
a = 5
DC =
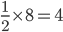
 is a right triangle. Hence
is a right triangle. Hence
 h = 3
h = 3Area of
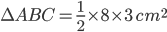
=
 Incorrect
Incorrect
a + a + 8 = 18
 a = 5
a = 5
DC =
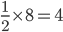
 is a right triangle. Hence
is a right triangle. Hence
 h = 3
h = 3Area of
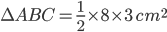
=

-
Question 4 of 50
4. Question
1 pointsEach square of a chess board has an area of
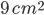 . Also the chess board has a margin of 3 cm around it. The side of the chess board is Correct
. Also the chess board has a margin of 3 cm around it. The side of the chess board is Correct
Side of each square of chess board =
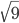
= 3 cm
Side of board =
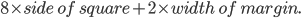
Side of board =

= 24 + 6 = 30 cm
Incorrect
Side of each square of chess board =
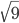
= 3 cm
Side of board =
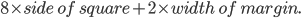
Side of board =

= 24 + 6 = 30 cm
-
Question 5 of 50
5. Question
1 pointsThe area of the quadratic of a circle whose circumference is 22 cm is
Correct


Area quadrant =
 Incorrect
Incorrect


Area quadrant =

-
Question 6 of 50
6. Question
1 pointsIf AB = 12 cm and BC = 5 cm the area of the shaded portion is (use
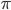 = 3.14)
= 3.14) Correct
Correct
BD =
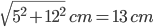
Also BD is diameter
 r = 6.5 cm
r = 6.5 cmRequired = Area of circle – area of rectangle
=
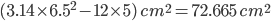 Incorrect
Incorrect
BD =
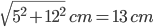
Also BD is diameter
 r = 6.5 cm
r = 6.5 cmRequired = Area of circle – area of rectangle
=
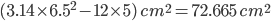
-
Question 7 of 50
7. Question
1 pointsPQRS is diameter of a circle of radius 6 cm such that PQ = OR = RS. Semicircles are drawn on PQ and QS as diameter as shown in figure. Area of the shaded region is
 Correct
Correct
Required area = area semicircle PS + area semicircle PQ – area semicircle QS
=
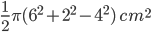
=
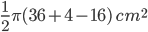
=
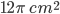 Incorrect
Incorrect
Required area = area semicircle PS + area semicircle PQ – area semicircle QS
=
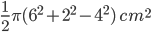
=
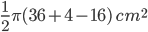
=
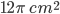
-
Question 8 of 50
8. Question
1 pointsA rectangular field has area equal to
 and perimeter 50 m. Its length and breadth respectively must beCorrect
and perimeter 50 m. Its length and breadth respectively must beCorrect
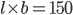
And 2(l + b) = 50
 l + b = 25
l + b = 25Clearly l = 15, b = 10
Incorrect
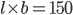
And 2(l + b) = 50
 l + b = 25
l + b = 25Clearly l = 15, b = 10
-
Question 9 of 50
9. Question
1 pointsA rectangular park is 46 m by 36 m. A path 2 m wide is built all around outside it. The cost of constructing these paths @ Rs. 50 per
 isCorrect
isCorrect
Area of path =
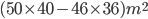
=

Cost = Rs.

= Rs. 17,200
Incorrect
Area of path =
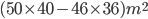
=

Cost = Rs.

= Rs. 17,200
-
Question 10 of 50
10. Question
1 pointsThe length of hypotenuse of a right angled triangle is 5 cm and its area is 6
 . The lengths of the remaining sides areCorrect
. The lengths of the remaining sides areCorrect
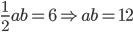

Use a + b =
 Incorrect
Incorrect
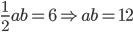

Use a + b =

-
Question 11 of 50
11. Question
1 pointsThe perimeter of a triangle is 450 m and its sides are in the ratio 13 : 12 : 5. The area of the triangle is
Correct
13x + 12 x + 5x = 450
X = 15
A = 195
B = 180
C = 75
Area =
 Incorrect
Incorrect
13x + 12 x + 5x = 450
X = 15
A = 195
B = 180
C = 75
Area =

-
Question 12 of 50
12. Question
1 pointsA circle has area which is 100 times the area of another circle. The ratio of their circumferences is
Correct

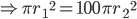

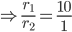

 Incorrect
Incorrect

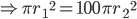

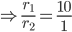


-
Question 13 of 50
13. Question
1 pointsFour equal circles of radius 7 cm touch each other as shown in figure. The area of the shaded part is
 Correct
Correct
Join centres to obtain a square of side 14 cm.
Incorrect
Join centres to obtain a square of side 14 cm.
-
Question 14 of 50
14. Question
1 pointsThe number of square tiles of side 20 cm are required to pave a footpath 1 m wide around a rectangular plot
 isCorrect
isCorrect
Area of foot path =
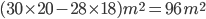

Number of tiles =
 Incorrect
Incorrect
Area of foot path =
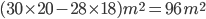

Number of tiles =

-
Question 15 of 50
15. Question
1 pointsIf each side of a rectangle is increased by 50%, its area will increase by
Correct
Original area =

New area =
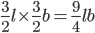
Increase % =

= 125%
Incorrect
Original area =

New area =
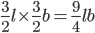
Increase % =

= 125%
-
Question 16 of 50
16. Question
1 pointsCircular disc of area
 is given. With its radius as diameter a circular disc of area
is given. With its radius as diameter a circular disc of area  is cut out of it. The area of the remaining disc is denoted by
is cut out of it. The area of the remaining disc is denoted by  . ThenCorrect
. ThenCorrect
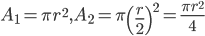
 Incorrect
Incorrect
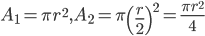

-
Question 17 of 50
17. Question
1 pointsA circular ground has a radius of 26 m. A 4 m wide road runs on the outside around it. The area of the road is (use
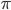 = 3.14)Correct
= 3.14)Correct
Area of road = 3.14
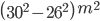
= 3.14 (30 + 26) (30 – 26)

= 703.36

 Incorrect
Incorrect
Area of road = 3.14
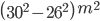
= 3.14 (30 + 26) (30 – 26)

= 703.36


-
Question 18 of 50
18. Question
1 pointsDiagonals of a rhombus are in the ratio 3 : 4 and its area is 2400
 . Side of the rhombus is Correct
. Side of the rhombus is Correct

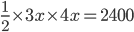

Use : side =
 Incorrect
Incorrect

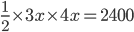

Use : side =

-
Question 19 of 50
19. Question
1 pointsAC is a diameter of circle with centre O. If BD
 at O and OA = 7 cm. Area of shaded region is
at O and OA = 7 cm. Area of shaded region is Correct
Correct
Required area = Area of smaller circle +

=

=
 Incorrect
Incorrect
Required area = Area of smaller circle +

=

=

-
Question 20 of 50
20. Question
1 pointsO is the centre of bigger circle and AC its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm, find area of shaded region.
 Correct
Correct
AC = 54 cm; BC = 10 cm
 AB = (54 – 10) cm = 44 cm
AB = (54 – 10) cm = 44 cmRadius of larger circle = 27 cm
Radius of smaller circle = 22 cm
Required area =

=
 Incorrect
Incorrect
AC = 54 cm; BC = 10 cm
 AB = (54 – 10) cm = 44 cm
AB = (54 – 10) cm = 44 cmRadius of larger circle = 27 cm
Radius of smaller circle = 22 cm
Required area =

=

-
Question 21 of 50
21. Question
1 pointsTwo card boards pieces in form of equilateral triangles having a side of 3 cm each are symmetrically glued to form a regular star as shown in the figure. The area of the star is
 Correct
Correct
Area of star =

is an equilateral triangle with each side equal to 1 cm.
 Incorrect
Incorrect
Area of star =

is an equilateral triangle with each side equal to 1 cm.

-
Question 22 of 50
22. Question
1 pointsABC is an equilateral
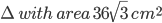 . The area of the inscribed circle is Correct
. The area of the inscribed circle is Correct
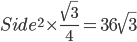
 side = 12 cm
side = 12 cmSemi-Perimeter =
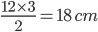
Use r =
 Incorrect
Incorrect
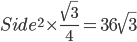
 side = 12 cm
side = 12 cmSemi-Perimeter =
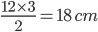
Use r =

-
Question 23 of 50
23. Question
1 pointsThe length of one diagonal of a rhombus is 80% of the other diagonal. The area of the rhombus is how many times the square of the length of the longer diagonal?
Correct
Let the length of the longer diagonal be L.
 Length of shorter diagonal = 80% of L =
Length of shorter diagonal = 80% of L = 
Area of rhombus =

 Incorrect
Incorrect
Let the length of the longer diagonal be L.
 Length of shorter diagonal = 80% of L =
Length of shorter diagonal = 80% of L = 
Area of rhombus =


-
Question 24 of 50
24. Question
1 pointsOABC is a rhombus whose vertices A, B and C lie on a circle with centre at O. If radius of circle is 10 cm then area of the rhombus
Correct
OA = OB = OC = AB = BC = 10 cm
Clearly
 are both equilateral and also congruent.
are both equilateral and also congruent.
Then area Rhombus =

=
 Incorrect
Incorrect
OA = OB = OC = AB = BC = 10 cm
Clearly
 are both equilateral and also congruent.
are both equilateral and also congruent.
Then area Rhombus =

=

-
Question 25 of 50
25. Question
1 points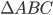 is an equilateral triangle with area
is an equilateral triangle with area  . With each vertex as centre a circle is described with radius equal to half the length of the said of the triangle. [Use
. With each vertex as centre a circle is described with radius equal to half the length of the said of the triangle. [Use 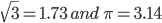 ] The area of the shaded part is
] The area of the shaded part is Correct
Correct
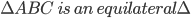
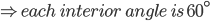
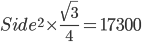
Side = 200 m
Radius of each circle = 100 m
Shaded area = area of
 - 3(area of any sector).Incorrect
- 3(area of any sector).Incorrect
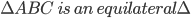
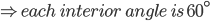
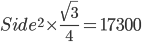
Side = 200 m
Radius of each circle = 100 m
Shaded area = area of
 - 3(area of any sector).
- 3(area of any sector). -
Question 26 of 50
26. Question
1 pointsIf both radius and heights of a cone are increased by 50%, then the volume of the cone will increase by
Correct


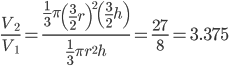
Volume increasing by
 Incorrect
Incorrect


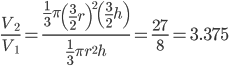
Volume increasing by

-
Question 27 of 50
27. Question
1 pointsIf both the height and the radius of the cone are doubled, then the ratio of volume of the bigger cone to that of the smaller cone will be
Correct

 Incorrect
Incorrect


-
Question 28 of 50
28. Question
1 pointsA cylindrical tub of radius 12 cm contains water to the height of 20 cm. A spherical iron ball is dropped into the tub. The ball gets completely immersed and the level of water is raised by 6.75 cm. The radius of the ball is
Correct
Radius of ball : r = ?; Radius of tube : R = 12 cm
H = 6.75 cm
Volume of ball = Volume of cylinder ABCD


 r= 9 cmIncorrect
r= 9 cmIncorrect
Radius of ball : r = ?; Radius of tube : R = 12 cm
H = 6.75 cm
Volume of ball = Volume of cylinder ABCD


 r= 9 cm
r= 9 cm -
Question 29 of 50
29. Question
1 pointsDiameter of a roller 60 m long is 42 cm. If it takes 700 complete revolutions to level a pay ground, the cost of leveling the play ground @ 45 p per square m is nearly
Correct
h = 42 cm; r = 30 cm, n = 700
Area leveled =

=
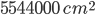
=
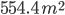
Cost = Rs.
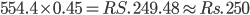 Incorrect
Incorrect
h = 42 cm; r = 30 cm, n = 700
Area leveled =

=
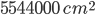
=
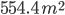
Cost = Rs.
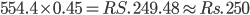
-
Question 30 of 50
30. Question
1 points2 cubes of each of side 12 cm are joined end to end. Volume of the resulting cuboid is
Correct

L = 24 cm, B = 12 cm, H = 12 cmV =
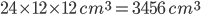 Incorrect
Incorrect

L = 24 cm, B = 12 cm, H = 12 cmV =
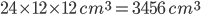
-
Question 31 of 50
31. Question
1 pointsA circus tent is cylindrical up to a height of 5 m and conical above it. If its diameter is 105 m and slant height of the conical portion is 53 m. The area of the canvas used to build the tent is
Correct
r =
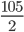 m; l = 53 m
m; l = 53 mH = 3 m

Area of canvas= C.S.A. cone + C.S.A. of cylindrical
=

=

=

=
 Incorrect
Incorrect
r =
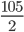 m; l = 53 m
m; l = 53 mH = 3 m

Area of canvas= C.S.A. cone + C.S.A. of cylindrical
=

=

=

=

-
Question 32 of 50
32. Question
1 pointsA solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and diameter of the cylinder is 7 cm. The S.A. of the solid is
Correct
r =

H + 2r = 19 cm
 h = 12 cm
h = 12 cm

Surface area =
=

=

=
 Incorrect
Incorrect
r =

H + 2r = 19 cm
 h = 12 cm
h = 12 cm

Surface area =
=

=

=

-
Question 33 of 50
33. Question
1 pointsThe radius of a sphere is increased by 100%, then the increase in surface area of the sphere will be
Correct
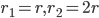

Increase in area = 300%
Incorrect
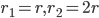

Increase in area = 300%
-
Question 34 of 50
34. Question
1 pointsDiameter of a cooper sphere is 6 cm. The sphere is melted and drawn into a wire of uniform circular cross section which is 72 cm long. The diameter of the wire is nearly
Correct
Volume of wire (cylinder) = Volume of sphere
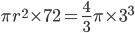


=

 Incorrect
Incorrect
Volume of wire (cylinder) = Volume of sphere
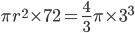


=


-
Question 35 of 50
35. Question
1 pointsThree cubes of edges 12 cm, 16 cm and 20 cm are melted and a new cube is made. The side of the new cube is
Correct

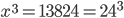
Side of new cube =24 cm
Incorrect

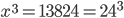
Side of new cube =24 cm
-
Question 36 of 50
36. Question
1 pointsThe cost of white washing the four walls of a room is Rs. 100. The cost of white washing a room twice in length and breadth but one fourth in height is
Correct
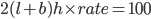

 required cost = Rs. 50Incorrect
required cost = Rs. 50Incorrect
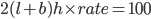

 required cost = Rs. 50
required cost = Rs. 50 -
Question 37 of 50
37. Question
1 pointsThe volume of a cylinder is
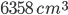 and its height is 28 cm. Its curved surface area is Correct
and its height is 28 cm. Its curved surface area is Correct


C.S.A. =
 Incorrect
Incorrect


C.S.A. =

-
Question 38 of 50
38. Question
1 pointsA hemispherical bowl is made of steel 12.1 cm thick. The inside radius of the bowl is 5 cm. The volume of steel used in making the bowl is nearly
Correct
r = 5 cm
R = (5 + 2.1) cm = 7.1
Volume of material =

=

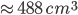 Incorrect
Incorrect
r = 5 cm
R = (5 + 2.1) cm = 7.1
Volume of material =

=

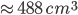
-
Question 39 of 50
39. Question
1 pointsA spherical balloon was deflated till its radius was halved. If its volume becomes n times its original volume then value of n is
Correct

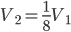 Incorrect
Incorrect

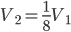
-
Question 40 of 50
40. Question
1 pointsThree cubes of edges 12 cm, 16 cm and 20 cm are melted and a new cube is made. The diagonal of the new cube is
Correct

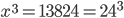
 Side of new cube = 24 cm
Side of new cube = 24 cm Incorrect
Incorrect

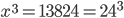
 Side of new cube = 24 cm
Side of new cube = 24 cm
-
Question 41 of 50
41. Question
1 pointsA rectangular sheet of area
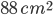 and length 8 cm is rolled along its breadth to make a hollow cylinder. The volume of this cylinder is Correct
and length 8 cm is rolled along its breadth to make a hollow cylinder. The volume of this cylinder is Correct
Circumference of cylinder = 88 cm
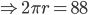

Also h = 8
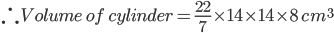
=
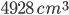 Incorrect
Incorrect
Circumference of cylinder = 88 cm
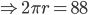

Also h = 8
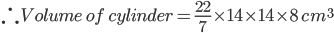
=
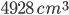
-
Question 42 of 50
42. Question
1 pointsCurved surface area of a cone whose volume is
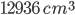 and the diameter of base is 42 cm, isCorrect
and the diameter of base is 42 cm, isCorrect
r =



L =

C.S.A. =

=
 Incorrect
Incorrect
r =



L =

C.S.A. =

=

-
Question 43 of 50
43. Question
1 pointsIf each side of a cube is tripped then its volume increases by
Correct
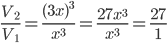
Increse in vol =
 = 27 -1 = 26
= 27 -1 = 26 increase % = 2600%Incorrect
increase % = 2600%Incorrect
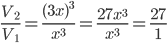
Increse in vol =
 = 27 -1 = 26
= 27 -1 = 26 increase % = 2600%
increase % = 2600% -
Question 44 of 50
44. Question
1 pointsA spherical ball was melted and made into smaller balls of half the radius of the original. The ratio of the sum total of the surface of all the smaller balls to that of the original ball is
Correct
Number of small balls =
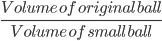
=

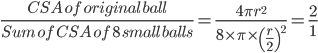
Or 2 : 1
Incorrect
Number of small balls =
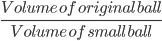
=

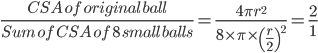
Or 2 : 1
-
Question 45 of 50
45. Question
1 pointsA cooper sphere of diameter 6 cm is drawn into a wire of diameter 0.4 cm. The length of the wire is
Correct
Volume wire (cyl) =Vol. of sphere
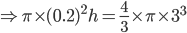
 Incorrect
Incorrect
Volume wire (cyl) =Vol. of sphere
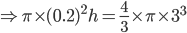

-
Question 46 of 50
46. Question
1 pointsRadii of two cylinder are in ratio 4 : 3 and their heights are in ratio 3 : 4. Ratio of their volumes is
Correct
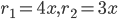

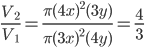 Incorrect
Incorrect
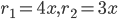

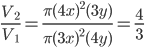
-
Question 47 of 50
47. Question
1 pointsThe curved surface area of a cylinder is
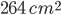 and its volume is
and its volume is 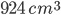 . The height of the cylinder is Correct
. The height of the cylinder is Correct

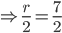


 Incorrect
Incorrect

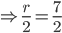



-
Question 48 of 50
48. Question
1 pointsThe circumference of edge of a hemispherical bowl is 132 cm. Its capacity is
Correct


Volume =
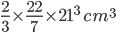
=
 Incorrect
Incorrect


Volume =
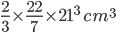
=

-
Question 49 of 50
49. Question
1 pointsThe radii of two right circular cylinder are in ratio 2 : 3 and their heights are in ratio 5 : 4. The ratio of their curved surface areas is
Correct
 Incorrect
Incorrect

-
Question 50 of 50
50. Question
1 pointsA vessel is in form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the base of the hemispherical bowl is 6 cm and the total height of the vessel is 11 cm. The capacity of the vessel is (Use
 = 3.14)Correct
= 3.14)Correct
r = 3 cm
H = (11 – 3) cm = 8 cm
Capacity of vessel =
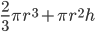
=

=

=

=
 Incorrect
Incorrect
r = 3 cm
H = (11 – 3) cm = 8 cm
Capacity of vessel =
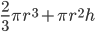
=

=

=

=


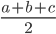


0 Comments