- Point: A fine dot on paper or a location on plane is called a point. A point has no length, breadth or thickness. Point is denoted by capital letters such as A, B or C etc.
- Line: The basic idea of line is staraightness. It has no breadth or thickness. It can be extended indefinitely in both directions. Line is denoted by small letters as l, m, n etc.
- Line Segment: Line segment is a part of line. It has two end points and a definite length.
- Ray: If a line segment is extended to unlimited length on one of the end point, we name it by a ray.
1) A line contains infinite points
2) Infinite lines can pass through a point
3) Two distinct lines in a plane can’t have more than one point common.
- Plane: A sheet of paper or surface of table has a flat surface. If we extend it in all directions to unlimited length, the extended flat surface is called a plane.
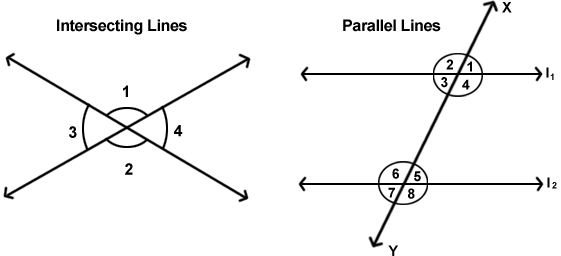
- Intersecting Lines: When two lines or line segments cross each other at a single point then they are called intersecting lines. When two lines intersect vertically opposite angles are equal.
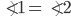
And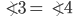
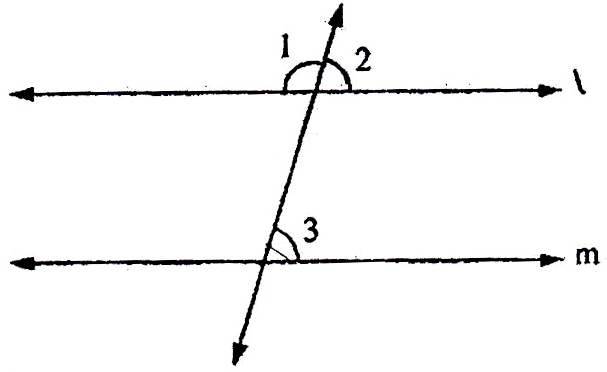
- Parallel Lines: Lines that never intersect and are always at equal distance from each other are called parallel lines.
In the above figure –
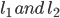 are parallel lines.
are parallel lines.
Lines XY is called transversal
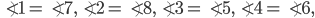 these angles are called alternate angles.
these angles are called alternate angles.
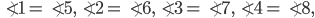 these angles are called corresponding angles.
these angles are called corresponding angles.
Types of Angles
- Acute Angle: An angle which is less than
 is called an acute angle.
is called an acute angle. - Right Angle: An agnle of
 is called right angle.
is called right angle. - Obstuse Angle: An angle which is lying between
 and
and 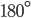 is called obtuse angle.
is called obtuse angle. - Straight Angle: An angle of
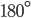 is called a straight angle.
is called a straight angle. - Reflex Angle: An angle which is lying between
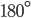 and
and  is called is a reflex angle.
is called is a reflex angle. - Complete Angle: An angle of
 is called complete angle.
is called complete angle. - Complementary Angle: Two angles whose sum is
 are called complementary angles.
are called complementary angles. - Supplementary Angle: Two angles whose sum is
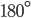 are called supplementary angle.
are called supplementary angle. - Adjacent Angles: Two angles are said to be adjacent if they have a common arm and same vertex. In figure given below
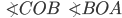 are adjacent angles
are adjacent angles

- Linear pair of Angles: Two adjacent angles form a linear pair of angle if their non-common arms are two opposite rays. Sumof angles of linear pair is always
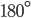 .
. - Triangle: A figure bounded by three line segments in a plane is called a triangle. It has three vertices, three sides and three angles.
Types of Triangles
- Acute Angled Triangle: when all three angles of triangle are acute then it is an acute angled triangle.
- Right Angled Triangle: When one angel of triangle
 then it is called right angled triangle.
then it is called right angled triangle. - Obtuse Angled Triangle: When one angle of the triangle is obtuse angle then triangle is called obtuse-angled triangle.
- Scalane Triangle: When all three sides of triangle are of different length then triangle is scalene triangle.
- Isoceles Triangle: When two sides of triangle are of equal length, then triangle is called isosceles. Two angles of isosceles triangle are also equal.
- Equilateral Triangle: It has all three sides of equal length. It has all three angles as
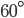 .
.
Properties of Triangle
- Sum of three angles of a triangle ar are always
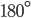 .
. - Sum of length of any two sides of a triangle is greater than the length of third side and difference of any two sides of a triangle is less than the third side.
- Side opposite to the greatest angle is the longest side.
- Sides opposite to equal angles are equal.
- The interior angles of a triangle (at each vertex) is equal to the sum of the two opposite interior angles.
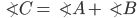
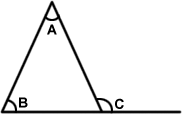
- Congreuent Triangles: Two triangles are said to be congruent if all sides and angles of one triangles are equal to corresponding sides and angles of another triangle.
Conditions:
Side-Side-side: If all three sides of one triangle are equal to the corresponding sides of another triangle then the two triangles are congruent.
Side-Angle-Side: If two sides and included angle of one triangle are equal to the corresponding sides and included angle of another triangle then triangles are congreuent.
Angle-Side-Angle: If two angles and included side of the one triangle are equal to two angles and included side of another triangle then triangles ar congrucent.
Right-hypotneuse-Side: If hypotenuse and one side of a right triangle is equal to hypotenuse and one side of another right triangle then triangles are congruent.
- Similar Triangles: Two triangles are said to be similar if they are alike in shapes only. The corresponding angles of two similar triangles are equal but the corresponding sides are only proportional and not equal.
Conditions:
The three angles of one triangle are respectively equal to the three angles of the second triangle.
Two sides of one triangle are proportional to two sides of the other and the included angles are equal.
a) Ratios of sides = Ratio of heights = Ratio of medians = Ratio of angular bisectors
b) Ratio of area = Ratio of square of corresponding sides
- Medians: The line segment joining a vertex of triangle to mid point of opposite side is called median.
Medians of triangle pass through a common point which divides each median in 2 : 1
It two median of a triangle are equal then triangle is isosceles. - Altitude: A line segment from a vertex which is perpendicular to opposite side of triangle is called altitude.
The sum of any two medians of a triangle is greater than the third median.
In a right triangle the square of hypotenuse is equal to sum of the squares of perpendicular and base (Pythogoras Theorem). - Quadrilateral: Any four sided closed figure in a plane is called a quadrilateral. Sum of four angles of a quadrilateral is always
 .
. - Trapezium: If one pair of opposite sides of a quadrilateral is parlled then it is called a trapezium.
- Parallelogram: A quadrilateral in which opposite sides are parallel is called a parallelogram.
In a Parallelogram –
1) Opposite sides are equal.
2) Opposite angles are equal.
3) Each diagonal divides the parallelogram into two congreuent triangles.
4) Sum of any two adjacent angels is.
5) Diagonals bisect each other.
- Rhombus: A rhombus is a parallelogram is which every pair of adjacent sides are equal. (i.e. all four sides are equal)
- Rectngle: A rectangle is a parallelogram in which all angles are
 .
.
Rectangle also satisfies all properties of parallelogram. In a rectangesl diagonals are equal. - Square: A square is a rectangle in which all four sides are equal.
All angles are
Diagonals are equal and bisect at right angle
When square inscribed in circle, diagonal becomes diameter of circle.
Circle
- A circle is a set of those points in a plane that are at a given constant distance from a given fixed point in the plane. The fixed point is O the centre and the given constant distance r is the radius.
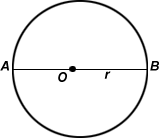
- A B is called diameter where diameter =
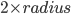
- Chord is a line which joins any two points on the circle.
- In a circle, the perpendicular from the centre to a chord bisects the chord.
- In a circle, the line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.
- In a circle, equal chords subtend equals angles at the centre.
- In a circle, chords which subtend equal angles at the centre are equal.
- Equal chords of a circle are equidistant from the centre.
- Chords of a circle which are equidistant from the centre are equal.
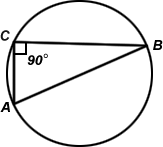
The angle in a semicircle is a right angle. The converse of the above is also true and is very useful in number of cases.
Important Questions for Geometry
Geometry



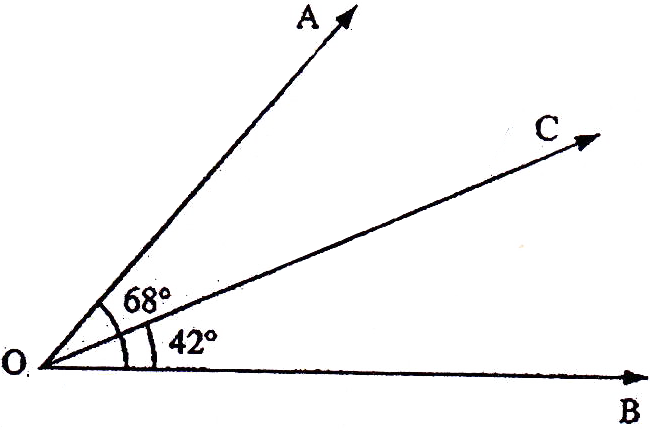



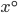


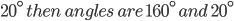

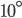
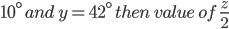

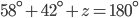




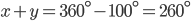
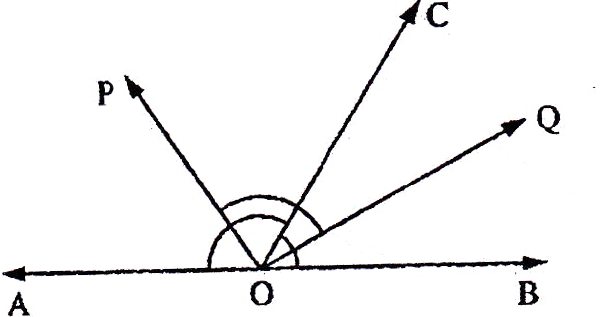
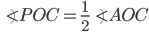

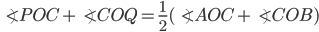


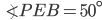

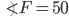

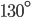




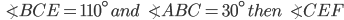

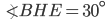


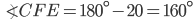



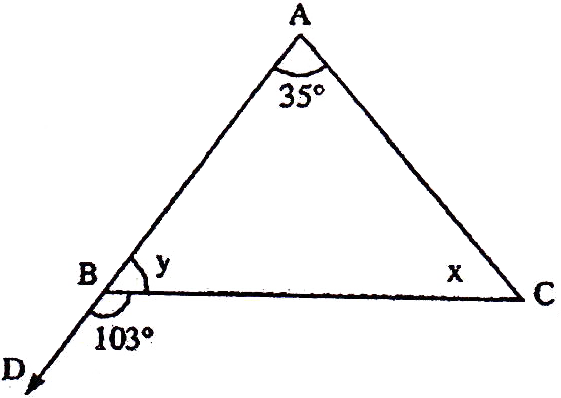
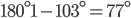
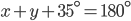
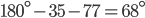
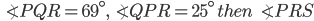
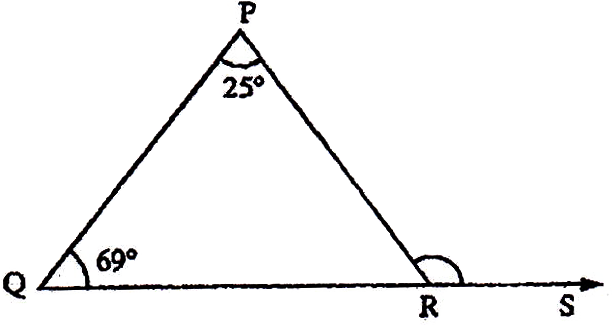


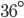

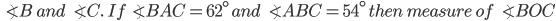
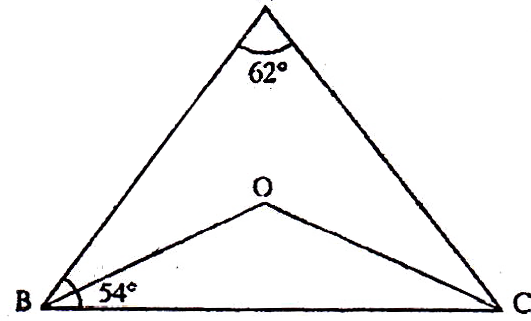
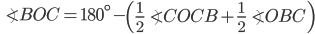



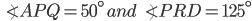





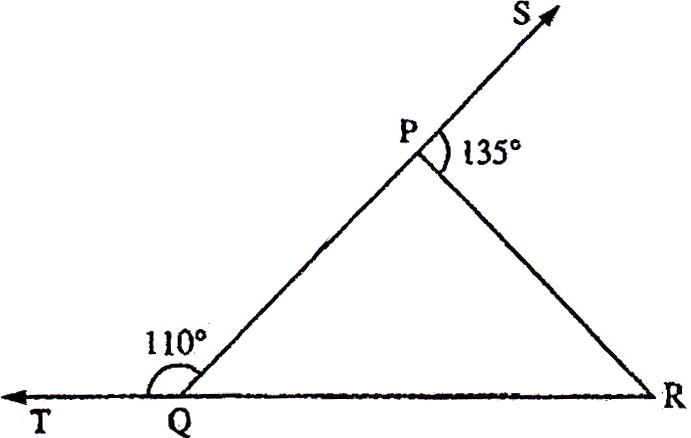
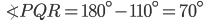


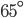
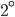
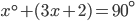
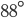

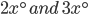
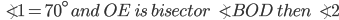
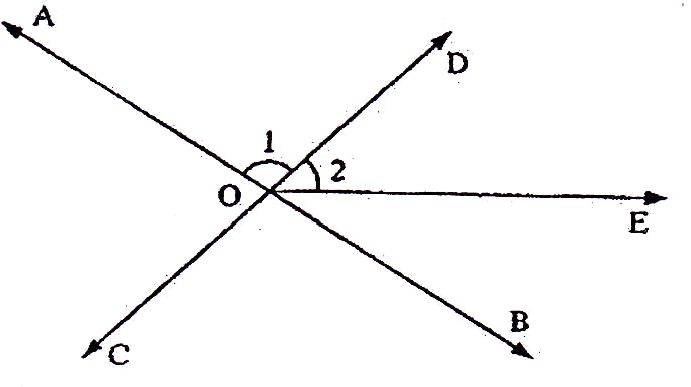

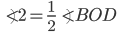
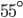

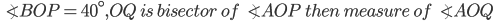
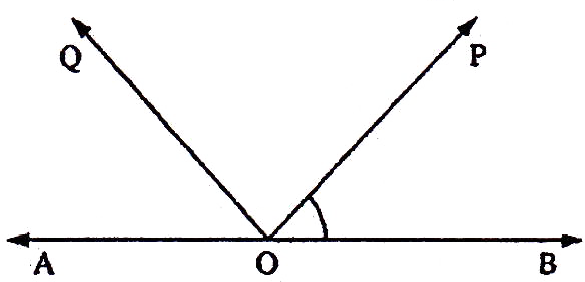

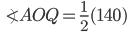
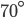
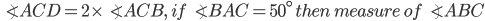
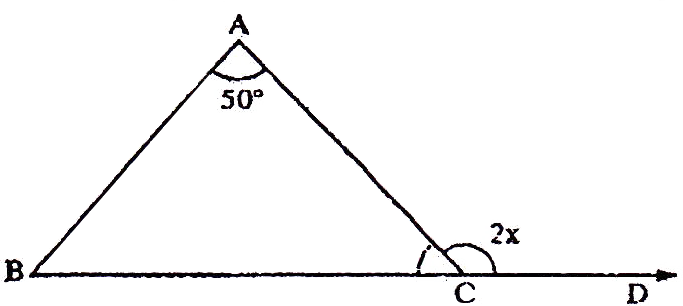
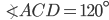


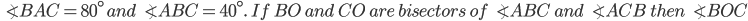
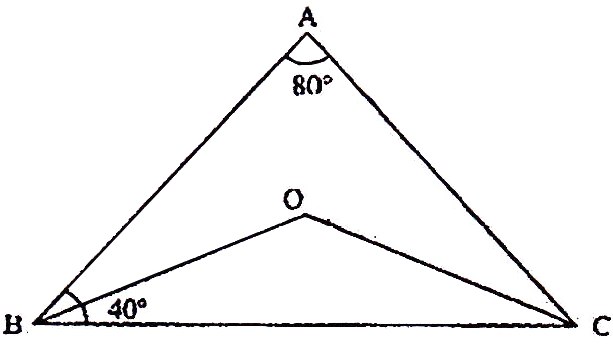
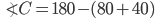
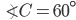
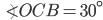
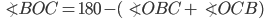
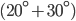


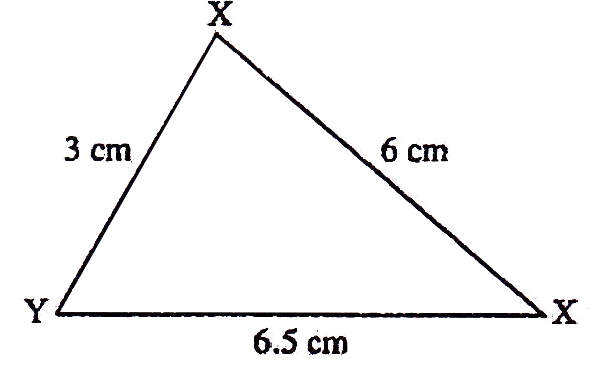
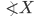

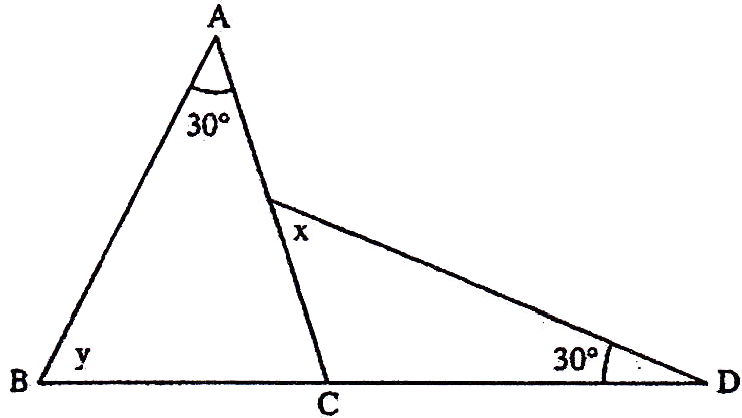
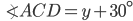


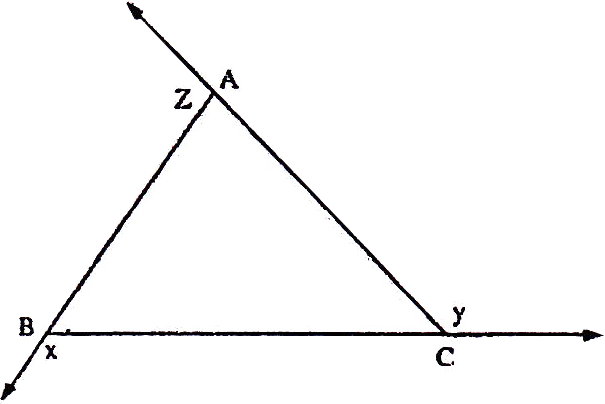
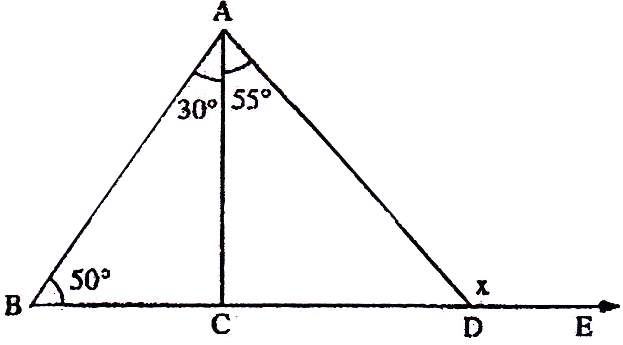
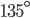
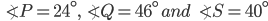




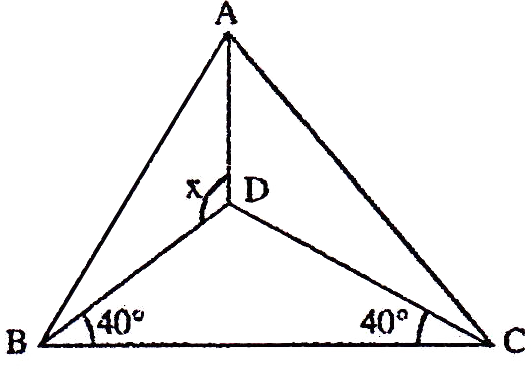

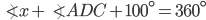



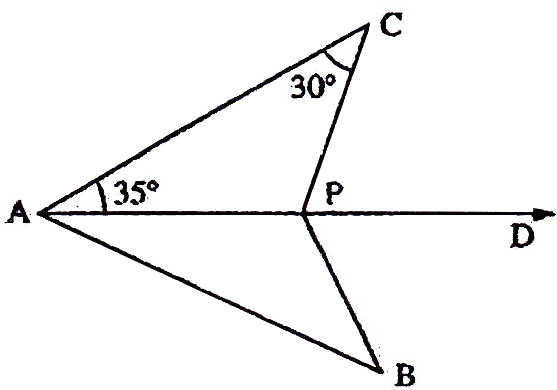
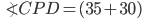

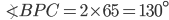
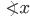

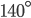
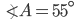
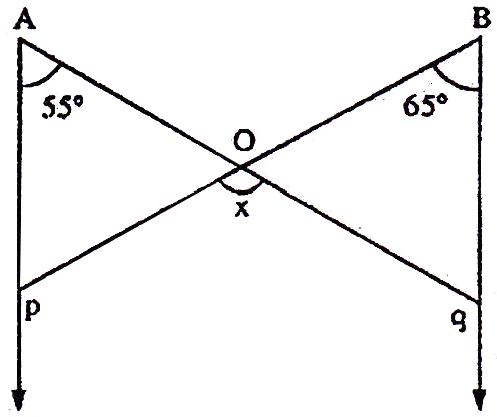



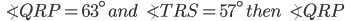
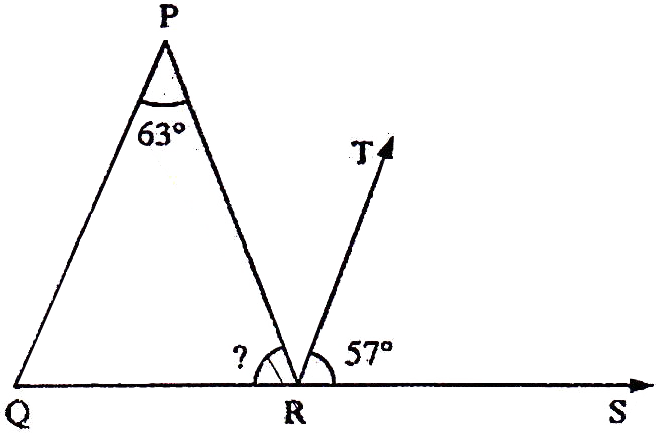
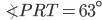
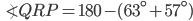
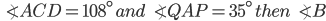
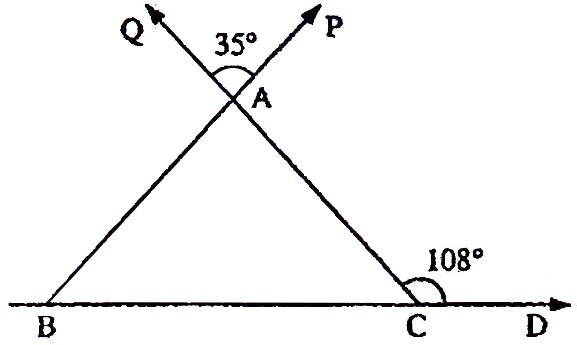
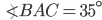
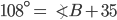
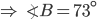

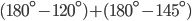
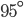
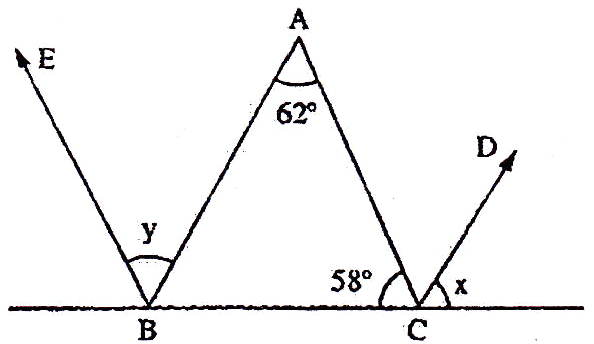
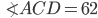
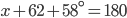


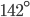


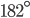



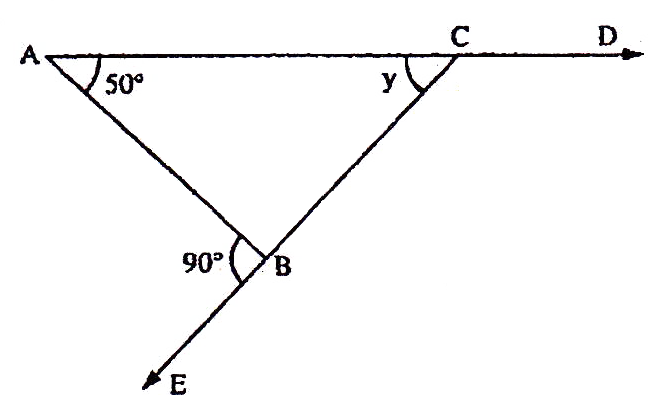
If the sides of an equilateral triangle are tripled, then find it's new area