Compound Interests Formulas and Shortcuts Tricks

COMPOUND INTEREST: The interest on interest is called compound interest. When the interest at the end of a specified period is added to the principal and the interest for the next period is calculated on the new principal, then it is called compound interest.

investing

Conversion Period: The fixed interval of time at the end of which the interest is calculated and added to the principal at the beginning of next interval of time, is called conversion period. In order words conversion period is the time at the end of which the interest is compounded. If the interest is compounded k times a year then the amount after n years is

$A= p\left ( 1+\frac{r}{k} \right )^{km}$
and compound interest C I = A - P

$\therefore\:\:\:CI= P\left [ \left ( 1+\frac{r}{k} \right )^{km}-1\right ]$

Where,	A = Amount
	C I = Compound interest
	P = Principal
	R = annual interest rate
	N = Number of years
	K = Number of conversion

If interest is compound annually then k = 1, if half yearly then k = 2, if quarterly then k = 4, if monthly then k = 12, if weekly then k = 52, and if daily then k = 365.

Nominal Rate and Effective Rate: The annual compound interest rate is called the nominal interest rate. When the interest is compound more than once in a year the actual percentage of interest per year is called the effective rate of interest.
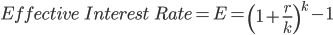
$Effective\:\:Interest\:\:Rate=E= \left ( 1+\frac{r}{k} \right )^{k}-1$

Where	r = nominal rate of interest,
	K = number of conversations
Also,	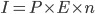$I= P\times E\times n$
Where	I = amount of interest,
	E = effective rate of interest in decimal,
	P = principal amount,
	n = time period.

Effective rate of interest is always greater than the nominal rate of interest.

Effective rate of interest is not related to the amount of principal.

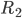If the interest rate is $R_{1}$ for the first year, $R_{2}$ for the second year, 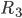$R_{3}$ for third year then.

Amount after 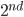$2^{nd}$ year = $p\left ( 1+\frac{R_{1}}{100} \right )\left ( 1+\frac{R_{2}}{100} \right )$

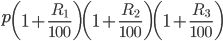
Amount after $3^{rd}$ year = $p\left ( 1+\frac{R_{1}}{100} \right )\left ( 1+\frac{R_{2}}{100} \right )\left ( 1+\frac{R_{3}}{100} \right )$

If V is the value of an item and if R is the rate of depreciation per year then the depreciated value of item after n years is obtained by
$V_{n}= V\left ( 1-\frac{R}{100} \right )^{n}$

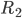When the rate of depreciation is $R_{1}$ for the first year, $R_{2}$ for the second year, 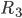$R_{3}$ for the third year then the depreciated value of that item after third year is

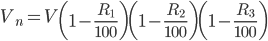
$V_{n}= V\left ( 1-\frac{R_{1}}{100} \right )\left ( 1-\frac{R_{2}}{100} \right )\left ( 1-\frac{R_{3}}{100} \right )$

ANNUITY: A series of equal and regular payments of a fixed sum of money made at equal interval of time is called annuity. Annuity may be of two types.

Annuity Regular: In this type the first payment or receipt is made at the end of the period.

Annuity Due or Annuity Immediate: In this type the first payment or receipt is made at the beginning of the period.

Future Value of Annuity: The amount to be paid or received as an annuity at the end of every fixed period, if the interest is added at compound rate of interest for the next period, is known as future value of annuity. It is the tomorrow’s value of today’s money compounded at the rate value of interest. Thus future value is the cash value of an investment at some time in future . In ordinary annuity each payment is made at the end of each payment period. Then the ordinary annuity of n payments of Rs. a each, where the interest rate is i per period is

$A= A(n,i)= \left [ \frac{(1+i)^{n}-1 }{i}\right ]$

In annuity due or annuity immediate the first receipt or payment is made at the beginning. Here the formula for the annuity is

$A=(1+i)\cdot A(n,i)$

$= (1+i)\cdot a\left [ \frac{(1+i)^{n}-1 }{i}\right ]$

Present value of Annuity: If the sum paid or received yearly or at an interval of certain period is computed with its present value, naturally the present value is less because of compounded factors. Present value is today’s value of tomorrow’s money discounted at the interest rate. If the annuity is payable or receivable at the end of year (Ordinary annuity) then the formula for present value is

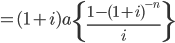
$= (1+i)a\left \{ \frac{1-(1+i)^{-n}}{i} \right \}$

$P= (1+i)P(n,1)$

If the annuity is payable or receivable at the beginning of year (annuity due) then the formula for present value is

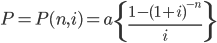
$P= P(n,i)= a\left \{ \frac{1-(1+i)^{-n}}{i} \right \}$
If the annuity is payable or receivable yearly on payment basis then
$P=\frac{a}{i}$
If the annuity is payable or receivable half yearly, quarterly, monthly or weekly then all the above formula can be adjusted to find out the present or future value of annuity. In such cases n is replaced by nk and i is replaced by i/k where k is the number of conversations.

SINKING FUND: It is fund created by a company to meet predetermined debts or certain liabilities out of their profit at the end of every accounting year. This fund is also known as pay back fund. This fund is invested elsewhere at a certain rate of interest and the proceeds of such interest is also reinvested again and again . When need arises this fund is disinvested and cash can be used to meet the fixed liability or to replace old units or business. The formula used for sinking fund is

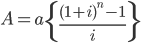
$A=a\left \{ \frac{(1+i)^{n}-1}{i} \right\}$

Solved Examples of Compound Interests

Example 1. A person deposited Rs.1,00,000 in his bank for 3 years at simple rate of 6%. How much would be the final value of deposit.

Solution : Here P=100000, n=3, r=0.06
Final value of deposit=P(1+rn)
= 100000(1+(0.06)(3))
= 118000

Example 2. Some part of Rs. 10000 was lent at 8% per year and remaining was deposited in bank at 6% per year. If the total simple interest from both the fractions in 3 years was Rs. 2160, calculate the amount lent at 8% per year.

Solution : Let x be the amount lent at 8% per year. Then (10000 - x) amount is deposited at 6% per year in bank.
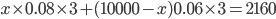
$x\times 0.08\times3 +(10000-x)0.06\times 3=2160$
$\therefore \:\:\:\:\:0.24x+1800-0.18x=2160$
$\therefore \:\:\:\:\:0.06x=360$
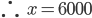
$\therefore \:\:\:\:\:x=6000$

Example 3. A certain sum of money amounts to Rs. 1500 in 2 years and to Rs. 1850 in 3.5 years. Find the sum and rate of interest.

Solution : Simple interest for 1.5 years = (1850 -1500) =350
Simple interest for two years =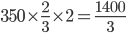 $350\times \frac{2}{3}\times 2=\frac{1400}{3}$
$\therefore \:\:\:\:\:$ Principle 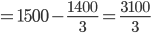$= 1500-\frac{1400}{3}=\frac{3100}{3}$
Now 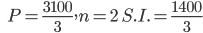$\:\:\:\:\:P= \frac{3100}{3},n=2\:\:S.I.= \frac{1400}{3}$
$\therefore \:\:\:\:\:$ Rate $= \left ( \frac{100\times \frac{3100}{3} }{\frac{1400}{3}\times 2}\right )$
$\therefore \:\:\:\:\:$ = 11.07 %

Example 4. Miss Krupati deposits a sum of Rs.200000 in a bank. After 2 years she withdraws Rs.100000. At the end of 5 years she received Rs.170000. Then find the rate of interest.

Solution : Simple interest on Rs.200000 for 2 years
$= 200000\times 2\times r= 400000r$

Simple interest on Rs.100000 for Next 3 years

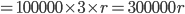
$= 100000\times 3\times r= 300000r$

Now, Interest = 170000 - 100000 = 70000

$\therefore$ 400000 - 300000r = 70000

$\therefore$ 700000r = 70000, r = 0.10

$\therefore$ Rate of interest = 10%

Important Questions on Compound Interests

IBPS questions related to Simple and Compound Interests

Question 1 of 18

1. Question
1 points
Mahesh invested an amount of Rs. 12050 at simple interest. He got an amount of Rs. 13496 at the end of 2 yr. At what rate of interest did he invest?
- 12% per annum
- 8% per annum
- 6% per annum
- 4.5% per annum
- None of these
Correct

Let the rate of interest be r% per annum.

$\therefore$ (13496 - 12050) = $\frac{12050\times 2}{100}$

$\Rightarrow r=\frac{1446 \times100}{12050 \times 2}$ = 6 % per annum

Incorrect

Let the rate of interest be r% per annum.

$\therefore$ (13496 - 12050) = $\frac{12050\times 2}{100}$

$\Rightarrow r=\frac{1446 \times100}{12050 \times 2}$ = 6 % per annum
Question 2 of 18

2. Question
5 points
If the difference between the simple and the compound interest earned on a sum of money at the rate of 5% per annum for 2 yr is Rs. 21, find the principal.
- Rs. 8000
- Rs. 8250
- Rs. 8400
- Cannot be deterrnined
- None of these
Correct

Let the principal be Rs. x

$\therefore\, \, \,21=x\left ( \frac{5}{100}\right )^{2}$

$\Rightarrow x = \frac{21 \times100 \times100}{5 \times5} = Rs. 8400$

Incorrect

Let the principal be Rs. x

$\therefore\, \, \,21=x\left ( \frac{5}{100}\right )^{2}$

$\Rightarrow x = \frac{21 \times100 \times100}{5 \times5} = Rs. 8400$
Question 3 of 18

3. Question
1 points
Sitaram invested an amount of Rs. 7450 @ 6% per annum rate of simple interest. After how many years will he obtain the total amount of Rs. 8791?
- 5 yr
- 3 yr
- 2 yr
- 6 yr
- None of these
Correct

$(8791 - 7450) = \frac{7450 \times6}{100}$

$\Rightarrow t = \frac{1341 \times100}{7450 \times6} = 3 yr$

Incorrect

$(8791 - 7450) = \frac{7450 \times6}{100}$

$\Rightarrow t = \frac{1341 \times100}{7450 \times6} = 3 yr$
Question 4 of 18

4. Question
1 points
Asmita invests an amount of Rs. 9535 @ 4% per annum to obtain a total amount of Rs. 11442 on simple interest after a certain period. For how many years did she invest the amount to obtain the total sum?
- 10 yr
- 2 yr
- 5 yr
- 4 yr
- None of these
Correct

$(11442 - 9535) =\frac{9535 \times4}{100}$

$\Rightarrow \, \,t = \frac{1907 \times100}{9535 \times4}=5\,yr$

Incorrect

$(11442 - 9535) =\frac{9535 \times4}{100}$

$\Rightarrow \, \,t = \frac{1907 \times100}{9535 \times4}=5\,yr$
Question 5 of 18

5. Question
1 points
Ms Suchi deposits an amount of Rs. 24000 to obtain a simple interest at the rate of 14 % per annum for 8 yr. What total amount will Ms Suchi get at the end of 8 yr?
- Rs. 52080
- Rs. 28000
- Rs. 50880
- Rs. 26880
- None of these
Correct

The amount which Suchi will get

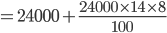
$= 24000 +\frac{24000 \times14 \times8}{100}$

$= 24000 + 26880 =Rs. 50880$

Incorrect

The amount which Suchi will get

$= 24000 +\frac{24000 \times14 \times8}{100}$

$= 24000 + 26880 =Rs. 50880$
Question 6 of 18

6. Question
1 points
What amount of compound interest can be obtained on an amount of Rs. 4500 at the rate of 4% per annum at the and end of 2 yr ?
- Rs. 360
- Rs.358.40
- Rs. 367.20
- None of these
Correct

Incorrect

$Compund \, \, Interest=4500\left [ \left ( 1+\frac{4}{100} \right )^{2}-1 \right ]$

$=4500\left [ \left ( \frac{26}{25} \right )^{2}-1 \right ]$

$=4500\left [ \frac{26^{2}-25^{2}}{25^{2}} \right ]$

$=4500\left [ \frac{\left ( 26-25 \right )\left ( 26+25 \right )}{625} \right ]$

$=4500\left [ \frac{\left ( 1 \right )\left ( 51 \right )}{625} \right ]=Rs \, \, 367.20$
Question 7 of 18

7. Question
1 points
What amount of compound interest can be obtained on an amount of Rs. 4800 @ 6 % per annum at the end of 2 yr?
- Rs. 544.96
- Rs. 576
- Rs. 593.28
- Rs. 588
- None of these
Correct

$Compund \, \, Interest=4800\left [ \left ( 1+\frac{6}{100} \right )^{2}-1 \right ]$

$=4800\left [ \left ( \frac{52}{50} \right )^{2}-1 \right ]$

$=4800\left [ \frac{53^{2}-50^{2}}{50^{2}} \right ]$

$=4800\left [ \frac{\left ( 53-50 \right )\left ( 53+50 \right )}{2500} \right ]$

$=4800\left [ \frac{\left ( 3 \right )\left ( 103 \right )}{2500} \right ]=\, \,Rs \, \,593.28$

Incorrect

$Compund \, \, Interest=4800\left [ \left ( 1+\frac{6}{100} \right )^{2}-1 \right ]$

$=4800\left [ \left ( \frac{52}{50} \right )^{2}-1 \right ]$

$=4800\left [ \frac{53^{2}-50^{2}}{50^{2}} \right ]$

$=4800\left [ \frac{\left ( 53-50 \right )\left ( 53+50 \right )}{2500} \right ]$

$=4800\left [ \frac{\left ( 3 \right )\left ( 103 \right )}{2500} \right ]=\, \,Rs \, \,593.28$
Question 8 of 18

8. Question
1 points
What would be the compound interest obtained on an amount of Rs. 2000 at the rate of 15% per annum after 3 yr?
- Rs. 1141.75
- Rs. 1209.75
- Rs. 1041.75
- Rs. 1248.75
- None of these
Correct

$Compund\,Interest=2000\left [ \left ( 1+\frac{15}{100} \right )^{3} -1\right ]$

$=2000\left [ \left ( \frac{23}{20} \right )^{3}-1 \right ]$

$=2000\left [ \frac{23^{3}-20^{3}}{20^{3}} \right ]$

$=2000\left [ \frac{12167-8000}{8000} \right ]$

$=2000\left [ \frac{4167}{8000} \right ]=\,Rs\,1041.75$

Incorrect

$Compund\,Interest=2000\left [ \left ( 1+\frac{15}{100} \right )^{3} -1\right ]$

$=2000\left [ \left ( \frac{23}{20} \right )^{3}-1 \right ]$

$=2000\left [ \frac{23^{3}-20^{3}}{20^{3}} \right ]$

$=2000\left [ \frac{12167-8000}{8000} \right ]$

$=2000\left [ \frac{4167}{8000} \right ]=\,Rs\,1041.75$
Question 9 of 18

9. Question
1 points
A sum of money doubles itself in 4 yr at compound interest. It will amount to 8 times itself at the same rate of interest in
- 18 yr
- 12 yr
- 16 yr
- 24 yr
- None of these
Correct

Incorrect

The sum doubles in 4 yr.
$\therefore$ It will be 8 times i.e.,2³, times in 3 x 4 = 12 yr
Question 10 of 18

10. Question
1 points
If the compound interest on a certain sum for 2yr at 3% per annum be Rs. 101.50, then the simple interest on the same sum at the same rate and for the same time will be
- Rs. 90
- Rs. 95.50
- Rs. 100
- Rs. 98.25
- None of these
Correct

Let the sum be Rs. x .

$\therefore 101.50=x\left [ \left ( 1+\frac{3}{100} \right )^{2}-1 \right ]$

$\Rightarrow \frac{1015}{10}=x\left [ \frac{103^{2}-100^{2}}{10000} \right ]$

$\Rightarrow \frac{1015}{10}=x.\frac{\left ( 3 \right )\left ( 203 \right )}{10000}$

$x=\frac{1015\times 1000}{3\times 203}=\frac{5000}{3}$

$\therefore\, Simple\,Interest=\frac{5000\times3\times 2}{3\times 1000}=Rs \, \, 100$

Incorrect

Let the sum be Rs. x .

$\therefore 101.50=x\left [ \left ( 1+\frac{3}{100} \right )^{2}-1 \right ]$

$\Rightarrow \frac{1015}{10}=x\left [ \frac{103^{2}-100^{2}}{10000} \right ]$

$\Rightarrow \frac{1015}{10}=x.\frac{\left ( 3 \right )\left ( 203 \right )}{10000}$

$x=\frac{1015\times 1000}{3\times 203}=\frac{5000}{3}$

$\therefore\, Simple\,Interest=\frac{5000\times3\times 2}{3\times 1000}=Rs \, \, 100$
Question 11 of 18

11. Question
1 points
Shivangi invested Rs. 15000 at the rate of interest of 10% per annum for 1 yr. If the interest is compounded every six months, what amount wilt shivang get,at the end of the year?
- Rs. 16537.50
- Rs. 16500
- Rs. 16525.50
- Rs. 18150
- None of these
Correct

$The\,amount=15000\left (1+\frac{\frac{10}{2}}{100} \right )^{1\times 2}$

$=15000\left ( 1+\frac{5}{100} \right )^{2}$

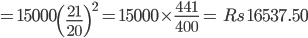
$=15000\left ( \frac{21}{20} \right )^{2}=15000\times \frac{441}{400}=\, \, Rs\, \, 16537.50$

Incorrect

$The\,amount=15000\left (1+\frac{\frac{10}{2}}{100} \right )^{1\times 2}$

$=15000\left ( 1+\frac{5}{100} \right )^{2}$

$=15000\left ( \frac{21}{20} \right )^{2}=15000\times \frac{441}{400}=\, \, Rs\, \, 16537.50$
Question 12 of 18

12. Question
1 points
The difference between CI and SI on a certain,sum at 4% for 3 yr is Rs. 608. The sum is
- Rs. 25000
- Rs.75000
- Rs. 100000
- Rs. 125000
- None of these
Correct

$608=P\left ( \frac{4+300}{100} \right )\left ( \frac{4}{100} \right )^{2}$

$\Rightarrow P=\frac{608\times 100\times 100\times 100}{304\times 16}=Rs\, 125000$

Incorrect

$608=P\left ( \frac{4+300}{100} \right )\left ( \frac{4}{100} \right )^{2}$

$\Rightarrow P=\frac{608\times 100\times 100\times 100}{304\times 16}=Rs\, 125000$
Question 13 of 18

13. Question
1 points
Ram invests Rs. 5000 in a bond which gives interest at 4%
per annum during the first year, 5% during the second year and 10% during the third year. How much does he get at the third year?

get at the end of the third Year?
- Rs. 5060
- Rs. 5900
- Rs. 6000
- Rs. 6006
- None of these
Correct

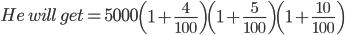
$He\, will \,get=5000\left ( 1+\frac{4}{100} \right )\left ( 1+\frac{5}{100} \right )\left ( 1+\frac{10}{100} \right )$

$=5000\left ( \frac{26}{25} \right )\left ( \frac{21}{20} \right )\left ( \frac{11}{10} \right ) = Rs \,6006$

Incorrect

$He\, will \,get=5000\left ( 1+\frac{4}{100} \right )\left ( 1+\frac{5}{100} \right )\left ( 1+\frac{10}{100} \right )$

$=5000\left ( \frac{26}{25} \right )\left ( \frac{21}{20} \right )\left ( \frac{11}{10} \right ) = Rs \,6006$
Question 14 of 18

14. Question
1 points
An amount of Rs. 25220 borrowed at 5% per annum, compounded yearly, is to be repaid in 3 equal instalments. The amount of each instalment is
- Rs. 9261
- Rs. 9100
- Rs. 9050
- Rs. 8930
- None of these
Correct

Let the amount of each installment be Rs x.

$\therefore \, \, \, 25220=\frac{x}{\left ( 1+\frac{5}{100} \right )}+\frac{x}{\left ( 1+\frac{5}{100} \right) ^{2}}+\frac{x}{\left ( 1+\frac{5}{100} \right ) ^{3}}$

$\Rightarrow \, \, 25220=x\left [ \frac{20}{21} +\left ( \frac{20}{21} \right )^{2}+\left ( \frac{20}{21} \right )^{3}\right]$

$\Rightarrow \, \, \, 25220=x\left ( \frac{20}{21} \right )\left [ 1+\frac{20}{21}+\frac{400}{441} \right ]$

$\Rightarrow \, \, \, 25220\times \frac{21}{20}=x\left [ \frac{441+420+400}{441} \right ]$

$\Rightarrow \, \, \, x=25220\times \frac{21}{20}\times \frac{441}{1261}=Rs\, 9261$

Incorrect

Let the amount of each installment be Rs x.

$\therefore \, \, \, 25220=\frac{x}{\left ( 1+\frac{5}{100} \right )}+\frac{x}{\left ( 1+\frac{5}{100} \right) ^{2}}+\frac{x}{\left ( 1+\frac{5}{100} \right ) ^{3}}$

$\Rightarrow \, \, 25220=x\left [ \frac{20}{21} +\left ( \frac{20}{21} \right )^{2}+\left ( \frac{20}{21} \right )^{3}\right]$

$\Rightarrow \, \, \, 25220=x\left ( \frac{20}{21} \right )\left [ 1+\frac{20}{21}+\frac{400}{441} \right ]$

$\Rightarrow \, \, \, 25220\times \frac{21}{20}=x\left [ \frac{441+420+400}{441} \right ]$

$\Rightarrow \, \, \, x=25220\times \frac{21}{20}\times \frac{441}{1261}=Rs\, 9261$
Question 15 of 18

15. Question
1 points
Aniket deposited two parts of a sum of Rs. 25000 in different banks at the rate of 15% per annum and 18% per annum respectively. In one year, he got Rs. 4050 as the total interest. What was the amount deposited at the rate of 18% Per annum?
- Rs. 9000
- Rs. 12000
- Rs. 15000
- Data inadequate
- None of these
Correct

Let Aniket invests Rs. x at the rate of 18 % per annum.

$\therefore$ $\frac{x\times18 \times1}{100} + \frac{(25000 - x) \times15 \times1 }{100} = 4050$

$\Rightarrow\, \,18x + 375000 - 15x = 405000$

$\Rightarrow \, \,3x = 405000 - 375000$

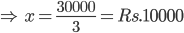
$\Rightarrow\, \,x = \frac{30000}{3} = Rs.10000$

Incorrect

Let Aniket invests Rs. x at the rate of 18 % per annum.

$\therefore$ $\frac{x\times18 \times1}{100} + \frac{(25000 - x) \times15 \times1 }{100} = 4050$

$\Rightarrow\, \,18x + 375000 - 15x = 405000$

$\Rightarrow \, \,3x = 405000 - 375000$

$\Rightarrow\, \,x = \frac{30000}{3} = Rs.10000$
Question 16 of 18

16. Question
1 points
The simple interest on a sum of money is 4/9 of the principal and the number of years is equal to the rate per cent per annum. The rate per annum is
- 5%
- 6%
Correct

Let the rate of interest and time be r% per annum and r yr respectively.

$\therefore \frac{4}{9}\times p=\frac{p\times r}{100}$

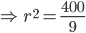
$\Rightarrow \, \, r^{2}=\frac{400}{9}$

$\Rightarrow\, \,r = \frac{20}{3} = 6\frac{2}{3}$ %

Incorrect

Let the rate of interest and time be r% per annum and r yr respectively.

$\therefore \frac{4}{9}\times p=\frac{p\times r}{100}$

$\Rightarrow \, \, r^{2}=\frac{400}{9}$

$\Rightarrow\, \,r = \frac{20}{3} = 6\frac{2}{3}$ %
Question 17 of 18

17. Question
1 points
A certain sum of money invested at compound interest, compounded annually, becomes Rs. 8820 in 2 yr and Rs. 9261 in 3 yr. The rate of interest is
- 5 % per annum
- 10% per annum
- 11 % per annum
- 12 % per annum
- None of these
Correct

Incorrect

Let the principal and rate of interest be P and r % per annum respectively.

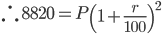
$\therefore \, \, 8820=P\left ( 1+\frac{r}{100} \right )^{2}$

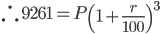
$\therefore \, \, 9261=P\left ( 1+\frac{r}{100} \right )^{3}$

From Equation (i) and (ii), we get

$\frac{9261}{8820}=1+\frac{r}{100}$

$\Rightarrow \, \, \, \frac{r}{100}=\frac{9261-8820}{8820}=\frac{441}{8820}$

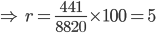
$\Rightarrow \, \, \, r=\frac{441}{8820}\times 100=5$ % $per\, \,annum$
Question 18 of 18

18. Question
1 points
In what time will Rs. 1000 becomes Rs. 1331 at 10% per annul compounded annually?
- o years
- 3 years
- 8 years
- 12 years
Correct

Principal = Rs. 1000; Amount = Rs. 1331; Rate = 10% p.a ,
Let the time be n years. Then,

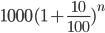
$1000(1+\frac{10}{100})^{n}$ =1331

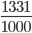
$(\frac{11}{100})^{n}$ = $\frac{1331}{1000}$ = $(\frac{11}{10})^{3}$

So, n = 3 years.

Incorrect

Principal = Rs. 1000; Amount = Rs. 1331; Rate = 10% p.a ,
Let the time be n years. Then,

$1000(1+\frac{10}{100})^{n}$ =1331

$(\frac{11}{100})^{n}$ = $\frac{1331}{1000}$ = $(\frac{11}{10})^{3}$

So, n = 3 years.