 The two words, “arithmetic reasoning,” strike terror into the hearts of people who have been out of school for a while or who have concentrated their studies in the humanities. The phrase “quantitative reasoning” is probably equally as terrifying as it is puzzling. The quantitative reasoning test includes arithmetic problems as well as questions asking test takers to evaluate a set of facts and conclusions to determine if the conclusions are true or false. Not all exams for special agent include this section, but it is very similar to the logical reasoning test. Practice this section in the short exercise below.
The two words, “arithmetic reasoning,” strike terror into the hearts of people who have been out of school for a while or who have concentrated their studies in the humanities. The phrase “quantitative reasoning” is probably equally as terrifying as it is puzzling. The quantitative reasoning test includes arithmetic problems as well as questions asking test takers to evaluate a set of facts and conclusions to determine if the conclusions are true or false. Not all exams for special agent include this section, but it is very similar to the logical reasoning test. Practice this section in the short exercise below.
For the straight arithmetic reasoning test, you do not need to understand intricate mathematical operations or to memorize complicated formulas. You can solve the problems arithmetically or by using some simple algebra.
Each problem is presented as a short verbal description of a situation that includes some numerical facts. You must read the problem to determine what the question is, if a series of calculations will be required, you do not want to stop short of the answer because you misinterpreted the question. Likewise, you do not waste time going beyond what is asked.
Once you have determined what the question asks, you must settle on the best route for arriving at the answer and set the problem up accordingly. Finally, you must perform the calculations. Some special agent exams will give you “none of these” as the fifth (E) choice, but the TEA has a fifth numerical choice. It is important that you perform all calculations carefully because an estimate or an approximation may lead you to choose the wrong answer.
Reminder: Do all the practice exercise questions with pencil on scratch paper. You will not be permitted to use a calculator at the exam, so get used to doing arithmetic without one. Answer questions in the practice exercise by circling the letter of your choice.
Solved Examples - Arithmetic Reasoning
Example 1) A police department purchases badges at 16$ each for all the graduates of the police training academy. The last training class graduated 10 new officers. What is the total amount of money the department will spend for badges for these new officers?
(A) $70
(B) $116
(C) $160
(D) $180
(E) $200
Solution: The correct answer is (C). It can be obtained by computing the following:

The badges are priced at 16$ each. The department must purchase 10 of them for the new officers. Multiplying the price of one badge (16$) by the number of graduates (10) gives the total price for all of the badges.
Choice (A), (B), and (D) are the result of erroneous computations.
Example 2) An investigator rented a car for six days and was charged 450$. The car rental company charged 35$ per day plus 0.30$ per mile driven. How many miles did the investigator drive the car?
Solution: The correct answer is (A). It can be obtained by computing the following:
6(35) + 0.30x = 450
The investigator rented the car for six days at 35$ per day, which is 210$; 210$ subtracted from the total charge of 450$ leaves 240$, the portion of the total charge which was expended for the miles driven. This amount divided by charge per mile  gives the number of miles (800) driven by the investigator.
gives the number of miles (800) driven by the investigator.
Choices (B), (C), and (D) are the result of erroneous computations.
Arithmetic Reasoning Questions from Previous Year Exams
Quiz-summary
0 of 77 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
Information
Verbal Reasoning : Arithmetic Reasoning
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 77 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- Answered
- Review
-
Question 1 of 77
1. Question
1 pointsThe total of the ages of Amar, Akbar and Anthony is 80 years. What was the total of their ages three years ago?
Correct
Required sum = (80 - 3
 3) years = (80 - 9) years = 71 years.Incorrect
3) years = (80 - 9) years = 71 years.Incorrect
Required sum = (80 - 3
 3) years = (80 - 9) years = 71 years.
3) years = (80 - 9) years = 71 years. -
Question 2 of 77
2. Question
1 pointsTwo bus tickets from city A to B and three tickets from city A to C cost Rs. 77 but three tickets from city A to B and two tickets from city A to C cost Rs. 73. What are the fares for cities B and C from A?
Correct
Let Rs. x be the fare of city B from city A and Rs. y be the fare of city C from city A.
Then, 2x + 3y = 77 ...(i) and
3x + 2y = 73 ...(ii)
Multiplying (i) by 3 and (ii) by 2 and subtracting, we get: 5y = 85 or y = 17.
Putting y = 17 in (i), we get: x = 13
Incorrect
Let Rs. x be the fare of city B from city A and Rs. y be the fare of city C from city A.
Then, 2x + 3y = 77 ...(i) and
3x + 2y = 73 ...(ii)
Multiplying (i) by 3 and (ii) by 2 and subtracting, we get: 5y = 85 or y = 17.
Putting y = 17 in (i), we get: x = 13
-
Question 3 of 77
3. Question
1 pointsAn institute organised a fete and 1/5 of the girls and 1/8 of the boys participated in the same. What fraction of the total number of students took part in the fete?
Correct
Incorrect
-
Question 4 of 77
4. Question
1 pointsA number of friends decided to go on a picnic and planned to spend Rs. 96 on eatables. Four of them, however, did not turn up. As a consequence, the remaining ones had to contribute Rs. 4 each extra. The number of those who attended the picnic was
Correct
Lets the number of person be x. then

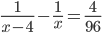


(x - 12) (x + 8) = 0
x = 12
so required number = x - 4 = 8
Incorrect
Lets the number of person be x. then

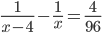


(x - 12) (x + 8) = 0
x = 12
so required number = x - 4 = 8
-
Question 5 of 77
5. Question
1 pointsA, B, C, D and E play a game of cards. A says to B, "If you give me three cards, you will have as many as E has and if I give you three cards, you will have as many as D has." A and B together have 10 cards more than what D and E together have. If B has two cards more than what C has and the total number of cards be 133, how many cards does B have?
Correct
Clearly, we have :
B - 3 = E ...(i)
B + 3 = D ...(ii)
A + B = D + E+10 ...(iii)
B = C + 2 ...(iv)
A + B + C + D + E= 133 ...(v)
From (i) and (ii), we have : 2 B = D + E ...(vi)
From (iii) and (vi), we have : A = B + 10 ...(vii)
Using (iv), (vi) and (vii) in (v), we get:
(B + 10) + B + (B - 2) + 2B = 133
5B = 125
B = 25.
Incorrect
Clearly, we have :
B - 3 = E ...(i)
B + 3 = D ...(ii)
A + B = D + E+10 ...(iii)
B = C + 2 ...(iv)
A + B + C + D + E= 133 ...(v)
From (i) and (ii), we have : 2 B = D + E ...(vi)
From (iii) and (vi), we have : A = B + 10 ...(vii)
Using (iv), (vi) and (vii) in (v), we get:
(B + 10) + B + (B - 2) + 2B = 133
5B = 125
B = 25.
-
Question 6 of 77
6. Question
1 pointsA pineapple costs Rs. 7 each. A watermelon costs Rs. 5 each. X spends Rs. 38 on these fruits. The number of pineapples purchased is
Correct
Lets the Number of pineapple and watermelon be x and y respectively
Then, 7x + 5y =38
or, 5y =(38 - 7x)
or,

Clearly y is whole number, only then(38- 7 x) is divided by 5
This happens when x = 4.
Incorrect
Lets the Number of pineapple and watermelon be x and y respectively
Then, 7x + 5y =38
or, 5y =(38 - 7x)
or,

Clearly y is whole number, only then(38- 7 x) is divided by 5
This happens when x = 4.
-
Question 7 of 77
7. Question
1 pointsA woman says, "If you reverse my own age, the figures represent my husband's age. He is, of course, senior to me and the difference between our ages is one-eleventh of their sum." The woman's age is
Correct
Let x and y be the ten's and unit's digits respectively of the numeral denoting the woman's age.
Then, woman's age = (10x + y) years; husband's age = (10y + x) years.
Therefore (10y + x)- (10x + y) =
 (10y + x + 10x + y)
(10y + x + 10x + y)(9y-9x) =
 (11y + 11x) = (x + y)
(11y + 11x) = (x + y)10x = 8y
x =
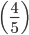 y
yClearly, y should be a single-digit multiple of 5, which is 5.
So, x = 4, y = 5.
Hence, woman's age = 10x + y = 45 years.
Incorrect
Let x and y be the ten's and unit's digits respectively of the numeral denoting the woman's age.
Then, woman's age = (10x + y) years; husband's age = (10y + x) years.
Therefore (10y + x)- (10x + y) =
 (10y + x + 10x + y)
(10y + x + 10x + y)(9y-9x) =
 (11y + 11x) = (x + y)
(11y + 11x) = (x + y)10x = 8y
x =
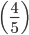 y
yClearly, y should be a single-digit multiple of 5, which is 5.
So, x = 4, y = 5.
Hence, woman's age = 10x + y = 45 years.
-
Question 8 of 77
8. Question
1 pointsA girl counted in the following way on the fingers of her left hand : She started by calling the thumb 1, the index finger 2, middle finger 3, ring finger 4, little finger 5 and then reversed direction calling the ring finger 6, middle finger 7 and so on. She counted upto 1994. She ended counting on which finger ?
Correct
Clearly, while counting, the numbers associated to the thumb will be : 1, 9,17, 25,.....
i.e. numbers of the form (8n + 1).
Since 1994 = 249 x 8 + 2, so 1993 shall correspond to the thumb and 1994 to the index finger.
Incorrect
Clearly, while counting, the numbers associated to the thumb will be : 1, 9,17, 25,.....
i.e. numbers of the form (8n + 1).
Since 1994 = 249 x 8 + 2, so 1993 shall correspond to the thumb and 1994 to the index finger.
-
Question 9 of 77
9. Question
1 pointsA man has Rs. 480 in the denominations of one-rupee notes, five-rupee notes and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has ?
Correct
Let number of notes of each denomination be x.
Then, x + 5x + 10x = 480
 16x = 480
16x = 480 x = 30.
x = 30.Hence, total number of notes = 3x = 90.
Incorrect
Let number of notes of each denomination be x.
Then, x + 5x + 10x = 480
 16x = 480
16x = 480 x = 30.
x = 30.Hence, total number of notes = 3x = 90.
-
Question 10 of 77
10. Question
1 pointsWhat is the product of all the numbers in the dial of a telephone ?
Correct
Since one of the numbers on the dial of a telephone is zero, so the product of all the numbers on it is 0.
Incorrect
Since one of the numbers on the dial of a telephone is zero, so the product of all the numbers on it is 0.
-
Question 11 of 77
11. Question
1 pointsA is 3 years older to B and 3 years younger to C, while B and D are twins. How many years older is C to D?
Correct
Since B and D are twins, so B = D.
Now, A = B + 3 and A = C - 3.
Thus, B + 3 = C - 3
 D + 3 = C-3
D + 3 = C-3 C - D = 6.Incorrect
C - D = 6.Incorrect
Since B and D are twins, so B = D.
Now, A = B + 3 and A = C - 3.
Thus, B + 3 = C - 3
 D + 3 = C-3
D + 3 = C-3 C - D = 6.
C - D = 6. -
Question 12 of 77
12. Question
1 pointsThe 30 members of a club decided to play a badminton singles tournament. Every time a member loses a game he is out of the tournament. There are no ties. What is the minimum number of matches that must be played to determine the winner?
Correct
Clearly, every member except one (i.e. the winner) must lose one game to decide the winner. Thus, minimum number of matches to be played = 30 - 1 = 29.
Incorrect
Clearly, every member except one (i.e. the winner) must lose one game to decide the winner. Thus, minimum number of matches to be played = 30 - 1 = 29.
-
Question 13 of 77
13. Question
1 pointsIn a garden, there are 10 rows and 12 columns of mango trees. The distance between the two trees is 2 metres and a distance of one metre is left from all sides of the boundary of the garden. The length of the garden is
Correct
Each row contains 12 plants.
There are 11 gapes between the two corner trees (11 x 2) metres and 1 metre on each side is left.
Therefore Length = (22 + 2) m = 24 m.
Incorrect
Each row contains 12 plants.
There are 11 gapes between the two corner trees (11 x 2) metres and 1 metre on each side is left.
Therefore Length = (22 + 2) m = 24 m.
-
Question 14 of 77
14. Question
1 points12 year old Manick is three times as old as his brother Rahul. How old will Manick be when he is twice as old as Rahul?
Correct
Manick's present age = 12 years, Rahul's present age = 4 years.
Let Manick be twice as old as Rahul after x years from now.
Then, 12 + x = 2 (4 + x)
 12 + x = 8 + 2x
12 + x = 8 + 2x x = 4.
x = 4.Hence, Manick's required age = 12 + x = 16 years.
Incorrect
Manick's present age = 12 years, Rahul's present age = 4 years.
Let Manick be twice as old as Rahul after x years from now.
Then, 12 + x = 2 (4 + x)
 12 + x = 8 + 2x
12 + x = 8 + 2x x = 4.
x = 4.Hence, Manick's required age = 12 + x = 16 years.
-
Question 15 of 77
15. Question
1 pointsA tailor had a number of shirt pieces to cut from a roll of fabric. He cut each roll of equal length into 10 pieces. He cut at the rate of 45 cuts a minute. How many rolls would be cut in 24 minutes ?
Correct
Number of cuts made to cut a roll into 10 pieces = 9.
Therefore Required number of rolls =
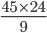 = 120.Incorrect
= 120.Incorrect
Number of cuts made to cut a roll into 10 pieces = 9.
Therefore Required number of rolls =
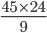 = 120.
= 120. -
Question 16 of 77
16. Question
1 pointsIn a class of 60 students, the number of boys and girls participating in the annual sports is in the ratio 3 : 2 respectively. The number of girls not participating in the sports is 5 more than the number of boys not participating in the sports. If the number of boys participating in the sports is 15, then how many girls are there in the class ?
Correct
Let the number of boys and girls participating in sports be 3x and 2x respectively.
Then, 3x = 15 or x = 5.
So, number of girls participating in sports = 2x = 10.
Number of students not participating in sports = 60 - (15 + 10) = 35.
Let number of boys not participating in sports be y.
Then, number of girls not participating in sports = (35 -y).
Therefore (35 - y) = y + 5
 2y
2y 30
30 y = 15.
y = 15.So, number of girls not participating in sports = (35 - 15) = 20.
Hence, total number of girls in the class = (10 + 20) = 30.
Incorrect
Let the number of boys and girls participating in sports be 3x and 2x respectively.
Then, 3x = 15 or x = 5.
So, number of girls participating in sports = 2x = 10.
Number of students not participating in sports = 60 - (15 + 10) = 35.
Let number of boys not participating in sports be y.
Then, number of girls not participating in sports = (35 -y).
Therefore (35 - y) = y + 5
 2y
2y 30
30 y = 15.
y = 15.So, number of girls not participating in sports = (35 - 15) = 20.
Hence, total number of girls in the class = (10 + 20) = 30.
-
Question 17 of 77
17. Question
1 pointsA man wears socks of two colours - Black and brown. He has altogether 20 black socks and 20 brown socks in a drawer. Supposing he has to take out the socks in the dark, how many must he take out to be sure that he has a matching pair ?
Correct
Since there are socks of only two colours, so two out of any three socks must always be of the same colour.
Incorrect
Since there are socks of only two colours, so two out of any three socks must always be of the same colour.
-
Question 18 of 77
18. Question
1 pointsA motorist knows four different routes from Bristol to Birmingham. From Birmingham to Sheffield he knows three different routes and from Sheffield to Carlisle he knows two different routes. How many routes does he know from Bristol to Carlisle ?
Correct
Total number of routes from Bristol to Carlisle = (4
 3
3  2) = 24.Incorrect
2) = 24.Incorrect
Total number of routes from Bristol to Carlisle = (4
 3
3  2) = 24.
2) = 24. -
Question 19 of 77
19. Question
1 pointsMac has £ 3 more than Ken, but then Ken wins on the horses and trebles his money, so that he now has £ 2 more than the original amount of money that the two boys had between them. How much money did Mac and Ken have between them before Ken's win?
Correct
Let money with Ken = x. Then, money with Mac = x + £ 3.
Now, 3x = (x + x + £ 3) + £ 2 x = £ 5.
Therefore Total money with Mac and Ken = 2x + £ 3 = £ 13
Incorrect
Let money with Ken = x. Then, money with Mac = x + £ 3.
Now, 3x = (x + x + £ 3) + £ 2 x = £ 5.
Therefore Total money with Mac and Ken = 2x + £ 3 = £ 13
-
Question 20 of 77
20. Question
1 pointsThere are deer and peacocks in a zoo. By counting heads they are 80. The number of their legs is 200. How many peacocks are there ?
Correct
Let x and y be the number of deer and peacocks in the zoo respectively. Then,
x + y = 80 ...(i) and
4x + 2y = 200 or 2x + y = 100 ...(ii)
Solving (i) and (ii), we get) x = 20, y = 60.
Incorrect
Let x and y be the number of deer and peacocks in the zoo respectively. Then,
x + y = 80 ...(i) and
4x + 2y = 200 or 2x + y = 100 ...(ii)
Solving (i) and (ii), we get) x = 20, y = 60.
-
Question 21 of 77
21. Question
1 pointsIn a class, there are 18 boys who are over 160 cm tall. If these constitute three-fourths of the boys and the total number of boys is two-thirds of the total number of students in the class, what is the number of girls in the class?
Correct
Let the number of boys be x. Then,
 x = 18 or x = 18 x
x = 18 or x = 18 x = 24.
= 24.If total number of students is y, then
 y = 24 or y = 24 x
y = 24 or y = 24 x = 36.
= 36.Therefore Number of girls in the class = (36 - 24) = 12.
Incorrect
Let the number of boys be x. Then,
 x = 18 or x = 18 x
x = 18 or x = 18 x = 24.
= 24.If total number of students is y, then
 y = 24 or y = 24 x
y = 24 or y = 24 x = 36.
= 36.Therefore Number of girls in the class = (36 - 24) = 12.
-
Question 22 of 77
22. Question
1 pointsA father is now three times as old as his son. Five years back, he was four times as old as his son. The age of the son (in years) is
Correct
Let son's age be x years. Then, father's age = (3x) years.
Five years ago, father's age = (3x - 5) years and son's age = (x - 5) years.
So, 3x - 5 = 4 (x - 5)
 3x - 5 = 4x - 20
3x - 5 = 4x - 20 x = 15.Incorrect
x = 15.Incorrect
Let son's age be x years. Then, father's age = (3x) years.
Five years ago, father's age = (3x - 5) years and son's age = (x - 5) years.
So, 3x - 5 = 4 (x - 5)
 3x - 5 = 4x - 20
3x - 5 = 4x - 20 x = 15.
x = 15. -
Question 23 of 77
23. Question
1 pointsA waiter's salary consists of his salary and tips. During one week his tips were 5/4 of his salary. What fraction of his income came from tips?
Correct
Lets Salary Be Rs. x Then tips = Rs

Total income =
 = Rs.
= Rs.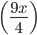
 Required Fraction =
Required Fraction = Incorrect
Incorrect
Lets Salary Be Rs. x Then tips = Rs

Total income =
 = Rs.
= Rs.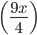
 Required Fraction =
Required Fraction =
-
Question 24 of 77
24. Question
1 pointsIf you write down all the numbers from 1 to 100, then how many times do you write 3?
Correct
Clearly, from 1 to 100, there are ten numbers with 3 as the unit's digit- 3, 13, 23, 33, 43, 53, 63, 73, 83, 93; and ten numbers with 3 as the ten's digit - 30, 31, 32, 33, 34, 35, 36, 37, 38, 39.
So, required number = 10 + 10 = 20.
Incorrect
Clearly, from 1 to 100, there are ten numbers with 3 as the unit's digit- 3, 13, 23, 33, 43, 53, 63, 73, 83, 93; and ten numbers with 3 as the ten's digit - 30, 31, 32, 33, 34, 35, 36, 37, 38, 39.
So, required number = 10 + 10 = 20.
-
Question 25 of 77
25. Question
1 pointsIf 100 cats kill 100 mice in 100 days, then 4 cats would kill 4 mice in how many days?
Correct
Less Cats more days (indirect proportion)
Less Mice less days (direct proportion)
Let's the required no of days be x
Cat 4 : 100 mice 100 : 4 } :: x: 100
 100
100 4
4 x =4
x =4 100
100 100
100or x =
 Incorrect
Incorrect
Less Cats more days (indirect proportion)
Less Mice less days (direct proportion)
Let's the required no of days be x
Cat 4 : 100 mice 100 : 4 } :: x: 100
 100
100 4
4 x =4
x =4 100
100 100
100or x =

-
Question 26 of 77
26. Question
1 pointsFive bells begin to toll together and toll respectively at intervals of 6, 5, 7, 10 and 12 seconds. How many times will they toll together in one hour excluding the one at the start?
Correct
L.C.M. of 6, 5, 7, 10 and 12 is 420.
So, the bells will toll together after every 420 seconds i.e. 7 minutes.
Now, 7
 8 = 56 and 7
8 = 56 and 7  9 = 63.
9 = 63.Thus, in 1-hour (or 60 minutes), the bells will toll together 8 times, excluding the one at the start.
Incorrect
L.C.M. of 6, 5, 7, 10 and 12 is 420.
So, the bells will toll together after every 420 seconds i.e. 7 minutes.
Now, 7
 8 = 56 and 7
8 = 56 and 7  9 = 63.
9 = 63.Thus, in 1-hour (or 60 minutes), the bells will toll together 8 times, excluding the one at the start.
-
Question 27 of 77
27. Question
1 pointsA bus starts from city X. The number of women in the bus is half of the number of men. In city Y, 10 men leave the bus and five women enter. Now, number of men and women is equal. In the beginning, how many passengers entered the bus?
Correct
Originally, let number of women = x. Then, number of men = 2x.
So, in city Y, we have : (2x - 10) = (x + 5) or x - 15.
Therefore Total number of passengers in the beginning = (x + 2x) = 3x = 45.
Incorrect
Originally, let number of women = x. Then, number of men = 2x.
So, in city Y, we have : (2x - 10) = (x + 5) or x - 15.
Therefore Total number of passengers in the beginning = (x + 2x) = 3x = 45.
-
Question 28 of 77
28. Question
1 pointsA, B, C, D and E play a game of cards. A says to B, "If you give me 3 cards, you will have as many as I have at this moment while if D takes 5 cards from you, he will have as many as E has." A and C together have twice as many cards as E has. B and D together also have the same number of cards as A and C taken together. If together they have 150 cards, how many cards has C got?
Correct
Clearly, we have :
A = B - 3 ...(i)
D + 5 = E ...(ii)
A + C = 2E ...(iii)
B + D = A + C = 2E ...(iv)
A + B + C + D + E=150 ...(v)
From (iii), (iv) and (v), we get: 5E = 150 or E = 30.
Putting E = 30 in (ii), we get: D = 25.
Putting E = 30 and D = 25 in (iv), we get: B = 35.
Putting B = 35 in (i), we get: A = 32.
Putting A = 32 and E = 30 in (iii), we get: C = 28.
Incorrect
Clearly, we have :
A = B - 3 ...(i)
D + 5 = E ...(ii)
A + C = 2E ...(iii)
B + D = A + C = 2E ...(iv)
A + B + C + D + E=150 ...(v)
From (iii), (iv) and (v), we get: 5E = 150 or E = 30.
Putting E = 30 in (ii), we get: D = 25.
Putting E = 30 and D = 25 in (iv), we get: B = 35.
Putting B = 35 in (i), we get: A = 32.
Putting A = 32 and E = 30 in (iii), we get: C = 28.
-
Question 29 of 77
29. Question
1 pointsA farmer built a fence around his square plot. He used 27 fence poles on each side of the square. How many poles did he need altogether?
Correct
Since each pole at the corner of the plot is common to its two sides, so we have :
Total number of poles needed = 27
 4 - 4 = 108 - 4 = 104.Incorrect
4 - 4 = 108 - 4 = 104.Incorrect
Since each pole at the corner of the plot is common to its two sides, so we have :
Total number of poles needed = 27
 4 - 4 = 108 - 4 = 104.
4 - 4 = 108 - 4 = 104. -
Question 30 of 77
30. Question
1 pointsIn a city, 40% of the adults are illiterate while 85% of the children are literate. If the ratio of the adults to that of the children is 2 : 3, then what percent of the population is literate?
Correct
Lets The number of Adult and children be 2x and 3x Respectively
The illiterate population = (100 - 40)% of 2x + 85% of 3x

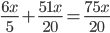
 Required Percentage
Required Percentage  Incorrect
Incorrect
Lets The number of Adult and children be 2x and 3x Respectively
The illiterate population = (100 - 40)% of 2x + 85% of 3x

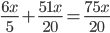
 Required Percentage
Required Percentage 
-
Question 31 of 77
31. Question
1 pointsA is three times as old as B. C was twice-as old as A four years ago. In four years' time, A will be 31. What are the present ages of B and C?
Correct
We have : A = 3B ...(i) and
C - 4 = 2 (A - 4) ...(ii)
Also, A + 4 = 31 or A= 31-4 = 27.
Putting A = 27 in (i), we get: B = 9.
Putting A = 27 in (ii), we get C = 50.
Incorrect
We have : A = 3B ...(i) and
C - 4 = 2 (A - 4) ...(ii)
Also, A + 4 = 31 or A= 31-4 = 27.
Putting A = 27 in (i), we get: B = 9.
Putting A = 27 in (ii), we get C = 50.
-
Question 32 of 77
32. Question
1 pointsToday is annu's birthday. One year, from today he will be twice as old as he was 12 years ago. How old is annu today?
Correct
Let annu age today = x years.
Then, Varan's age after 1 year = (x + 1) years.
Therefore x + 1 = 2 (x - 12)
 x + 1 = 2x - 24
x + 1 = 2x - 24 x = 25.Incorrect
x = 25.Incorrect
Let annu age today = x years.
Then, Varan's age after 1 year = (x + 1) years.
Therefore x + 1 = 2 (x - 12)
 x + 1 = 2x - 24
x + 1 = 2x - 24 x = 25.
x = 25. -
Question 33 of 77
33. Question
1 pointsA bird shooter was ask how many birds he had in the bag. He replied that there were all sparrows but six, all pigeons but six, and all ducks but six. How many birds he had in the bag in all?
Correct
There were all sparrows but six' means that six birds were not sparrows but only pigeons and ducks.
Similarly, number of sparrows + number of ducks = 6 and number of sparrows + number of pigeons = 6.
This is possible when there are 3 sparrows, 3 pigeons and 3 ducks i.e. 9 birds in all.
Incorrect
There were all sparrows but six' means that six birds were not sparrows but only pigeons and ducks.
Similarly, number of sparrows + number of ducks = 6 and number of sparrows + number of pigeons = 6.
This is possible when there are 3 sparrows, 3 pigeons and 3 ducks i.e. 9 birds in all.
-
Question 34 of 77
34. Question
1 pointsMr. Johnson was to earn £ 300 and a free holiday for seven weeks' work. He worked for only 4 weeks and earned £ 30 and a free holiday. What was the value of the holiday?
Correct
Let's the value of holiday be x
Then, pay the seven week's works = £300 + x
so,
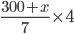
 £1200 + 4x = £210 + 7x
£1200 + 4x = £210 + 7x 3x = £990
3x = £990 x = £330Incorrect
x = £330Incorrect
Let's the value of holiday be x
Then, pay the seven week's works = £300 + x
so,
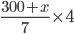
 £1200 + 4x = £210 + 7x
£1200 + 4x = £210 + 7x 3x = £990
3x = £990 x = £330
x = £330 -
Question 35 of 77
35. Question
1 pointsThree friends had dinner at a restaurant. When the bill was received, Amita paid
 as much as Veena paid and Veena paid
as much as Veena paid and Veena paid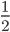 as much as Tanya paid. What faction of the bill did Veena pay?Correct
as much as Tanya paid. What faction of the bill did Veena pay?Correct
Let's Tanya Share = Rs. x Then Veena's Share Rs.

Total Bill = Rs.
 = Rs.
= Rs. 
Amita's Share = Rs.
 =Rs.
=Rs. 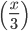
 Required Fraction =
Required Fraction =  Incorrect
Incorrect
Let's Tanya Share = Rs. x Then Veena's Share Rs.

Total Bill = Rs.
 = Rs.
= Rs. 
Amita's Share = Rs.
 =Rs.
=Rs. 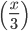
 Required Fraction =
Required Fraction = 
-
Question 36 of 77
36. Question
1 pointsIn a class, 20% of the members own only two cars each, 40% of the remaining own three cars each and the remaining members own only one car each. Which of the following statements is definitely true from the given statements?
Correct
Let total number of members be 100,
Then, number of members owning only 2 cars = 20.
Number of members owning 3 cars = 40% of 80 = 32.
Number of members owning only 1 car = 100 - (20 + 32) = 48.
Thus, 48% of the total members own one car each.
Incorrect
Let total number of members be 100,
Then, number of members owning only 2 cars = 20.
Number of members owning 3 cars = 40% of 80 = 32.
Number of members owning only 1 car = 100 - (20 + 32) = 48.
Thus, 48% of the total members own one car each.
-
Question 37 of 77
37. Question
1 pointsWhen Rahul was born, his father was 32 years older than his brother and his mother was 25 years older than his sister. If Rahul's brother is 6 years older than him and his mother is 3 years younger than his father, how old was Rahul's sister when he was born?
Correct
When Rahul was born, his brother's age = 6 years;
his father's age = (6 + 32) years = 38 years, his mother's age = (38 - 3) years = 35 years;
his sister's age = (35 - 25) years = 10 years.
Incorrect
When Rahul was born, his brother's age = 6 years;
his father's age = (6 + 32) years = 38 years, his mother's age = (38 - 3) years = 35 years;
his sister's age = (35 - 25) years = 10 years.
-
Question 38 of 77
38. Question
1 pointsA certain number of horses and an equal number of men are going somewhere. Half of the owners are on their horses' back while the remaining ones are walking along leading their horses. If the number of legs walking on the ground is 70, how many horses are there?
Correct
Let number of horses = number of men = x.
Then, number of legs = 4x + 2x
 = 5x.
= 5x.So, 5x = 70 or x = 14.
Incorrect
Let number of horses = number of men = x.
Then, number of legs = 4x + 2x
 = 5x.
= 5x.So, 5x = 70 or x = 14.
-
Question 39 of 77
39. Question
1 pointsRavi's brother is 3 years senior to him. His father was 28 years of age when his sister was born while his mother was 26 years of age when he was born. If his sister was 4 years of age when his brother was born, what were the ages of Ravi's father and mother respectively when his brother was born?
Correct
When Ravi's brother was born, let Ravi's father's age = x years and mother's age = y years.
Then, sister's age = (x - 28) years. So, x - 28 = 4 or x = 32.
Ravi's age = (y - 26) years. Age of Ravi's brother = (y - 26 + 3) years = (y - 23) years.
Now, when Ravi's brother was born, his age = 0 i.e. y - 23 = 0 or y = 23.
Incorrect
When Ravi's brother was born, let Ravi's father's age = x years and mother's age = y years.
Then, sister's age = (x - 28) years. So, x - 28 = 4 or x = 32.
Ravi's age = (y - 26) years. Age of Ravi's brother = (y - 26 + 3) years = (y - 23) years.
Now, when Ravi's brother was born, his age = 0 i.e. y - 23 = 0 or y = 23.
-
Question 40 of 77
40. Question
1 pointsThe number of boys in a class is three times the number of girls. Which one of the following numbers cannot represent the total number of children in the class?
Correct
Let number of girls = x and number of boys = 3x.
Then, 3x + x = 4x = total number of students.
Thus, to find exact value of x, the total number of students must be divisible by 4.
Incorrect
Let number of girls = x and number of boys = 3x.
Then, 3x + x = 4x = total number of students.
Thus, to find exact value of x, the total number of students must be divisible by 4.
-
Question 41 of 77
41. Question
1 pointsIn a family, the father took
 of the cake and he had 3 times as much as each of the other members had. The total number of family members isCorrect
of the cake and he had 3 times as much as each of the other members had. The total number of family members isCorrect
Let's there be (x + 1) Member.
Then, Father's Share =
 Share of each other member =
Share of each other member =
 3
3  =
=
 4x = 36
4x = 36 x = 9
x = 9Hence, total number of family Members = 10
Incorrect
Let's there be (x + 1) Member.
Then, Father's Share =
 Share of each other member =
Share of each other member =
 3
3  =
=
 4x = 36
4x = 36 x = 9
x = 9Hence, total number of family Members = 10
-
Question 42 of 77
42. Question
1 pointsIn three colored boxes - Red, Green and Blue, 108 balls are placed. There are twice as many balls in the green and red boxes combined as there are in the blue box and twice as many in the blue box as there are in the red box. How many balls are there in the green box?
Correct
Let R, G and B represent the number of balls in red, green and blue boxes respectively.
Then, .
R + G + B = 108 ...(i),
G + R = 2B ...(ii)
B = 2R ...(iii)
From (ii) and (iii), we have G + R = 2x 2R = 4R or G = 3R.
Putting G = 3R and B = 2R in (i), we get:
R + 3R + 2R = 108
 6R = 108
6R = 108  R = 18.
R = 18.Therefore Number of balls in green box = G = 3R = (3 x 18) = 54.
Incorrect
Let R, G and B represent the number of balls in red, green and blue boxes respectively.
Then, .
R + G + B = 108 ...(i),
G + R = 2B ...(ii)
B = 2R ...(iii)
From (ii) and (iii), we have G + R = 2x 2R = 4R or G = 3R.
Putting G = 3R and B = 2R in (i), we get:
R + 3R + 2R = 108
 6R = 108
6R = 108  R = 18.
R = 18.Therefore Number of balls in green box = G = 3R = (3 x 18) = 54.
-
Question 43 of 77
43. Question
1 pointsIn a cricket match, five batsmen A, B, C, D and E scored an average of 36 runs. D Scored 5 more than E; E scored 8 fewer than A; B scored as many as D and E combined; and B and C scored 107 between them. How many runs did E score?
Correct
Total runs scored = (36 x 5) = 180.
Let the runs scored by E be x.
Then, runs scored by D = x + 5; runs scored by A = x + 8;
runs scored by B = x + x + 5 = 2x + 5;
runs scored by C = (107 - B) = 107 - (2x + 5) = 102 - 2x.
So, total runs = (x + 8) + (2x + 5) + (102 - 2x) + (x + 5) + x = 3x + 120.
Therefore 3x + 120 =180
 3x = 60
3x = 60  x = 20.Incorrect
x = 20.Incorrect
Total runs scored = (36 x 5) = 180.
Let the runs scored by E be x.
Then, runs scored by D = x + 5; runs scored by A = x + 8;
runs scored by B = x + x + 5 = 2x + 5;
runs scored by C = (107 - B) = 107 - (2x + 5) = 102 - 2x.
So, total runs = (x + 8) + (2x + 5) + (102 - 2x) + (x + 5) + x = 3x + 120.
Therefore 3x + 120 =180
 3x = 60
3x = 60  x = 20.
x = 20. -
Question 44 of 77
44. Question
1 pointsThe total number of digits used in numbering the pages of a book having 366 pages is
Correct
Total number of digits
= (No. of digits in 1- digit page nos. + No. of digits in 2-digit page nos. + No. of digits in 3- digit page nos.)
= (1
 9 + 2
9 + 2  90 + 3
90 + 3  267) = (9 + 180 + 801) = 990.Incorrect
267) = (9 + 180 + 801) = 990.Incorrect
Total number of digits
= (No. of digits in 1- digit page nos. + No. of digits in 2-digit page nos. + No. of digits in 3- digit page nos.)
= (1
 9 + 2
9 + 2  90 + 3
90 + 3  267) = (9 + 180 + 801) = 990.
267) = (9 + 180 + 801) = 990. -
Question 45 of 77
45. Question
1 pointsIn a family, each daughter has the same number of brothers as she has sisters and each son has twice as many sisters as he has brothers. How many sons are there in the family
Correct
Let d and s represent the number of daughters and sons respectively.
Then, we have :
d - 1 = s and 2 (s - 1) = d.
Solving these two equations, we get: d = 4, s = 3.
Incorrect
Let d and s represent the number of daughters and sons respectively.
Then, we have :
d - 1 = s and 2 (s - 1) = d.
Solving these two equations, we get: d = 4, s = 3.
-
Question 46 of 77
46. Question
1 pointsAt a dinner party every two guests used a bowl of rice between them, every three guests used a bowl of dal between them and every four used a bowl of meat between them. There were altogether 65 dishes. How many guests were present at the party?
Correct
Let's the member of guests be x Then,
Number of Bowls of Rice =

Number of Bowls of Dal =

Number Of Bowls of Meats =





 13x = 65
13x = 65  12
12 x =
x = Incorrect
Incorrect
Let's the member of guests be x Then,
Number of Bowls of Rice =

Number of Bowls of Dal =

Number Of Bowls of Meats =





 13x = 65
13x = 65  12
12 x =
x =
-
Question 47 of 77
47. Question
1 pointsAyush was born two years after his father's marriage. His mother is five years younger than his father but 20 years older than Ayush who is 10 years old. At what age did the father get married?
Correct
Ayush's present age = 10 years.
His mother's present age = (10 + 20) years = 30 years.
Ayush's father's present age = (30 + 5) years = 35 years.
Ayush's father's age at the time of Ayush's birth = (35 - 10) years = 25 years.
Therefore Ayush's father's age at the time of marriage = (25 - 2) years = 23 years.
Incorrect
Ayush's present age = 10 years.
His mother's present age = (10 + 20) years = 30 years.
Ayush's father's present age = (30 + 5) years = 35 years.
Ayush's father's age at the time of Ayush's birth = (35 - 10) years = 25 years.
Therefore Ayush's father's age at the time of marriage = (25 - 2) years = 23 years.
-
Question 48 of 77
48. Question
1 pointsA student got twice as many sums wrong as he got right. If he attempted 48 sums in all, how many did he solve correctly?
Correct
Suppose the boy got x sums right and 2x sums wrong.
Then, x + 2x = 48
 3x = 48
3x = 48  x = 16.Incorrect
x = 16.Incorrect
Suppose the boy got x sums right and 2x sums wrong.
Then, x + 2x = 48
 3x = 48
3x = 48  x = 16.
x = 16. -
Question 49 of 77
49. Question
1 pointsDavid gets on the elevator at the 11th floor of a building and rides up at the rate of 57 floors per minute. At the same time, Albert gets on an elevator at the 51st floor of the same building and rides down at the rate of 63 floors per minute. If they continue travelling at these rates, then at which floor will their paths cross ?
Correct
Support their paths cross after x minutes.
Then, 11 + 57x = 51 - 63x
 120x = 40
120x = 40
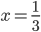
Number of Floors covered by David in
 min =
min = =19
=19so there paths cross at (11 + 19)th that is 30th floors.
Incorrect
Support their paths cross after x minutes.
Then, 11 + 57x = 51 - 63x
 120x = 40
120x = 40
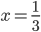
Number of Floors covered by David in
 min =
min = =19
=19so there paths cross at (11 + 19)th that is 30th floors.
-
Question 50 of 77
50. Question
1 pointsI have a few sweets to be distributed. If I keep 2, 3 or 4 in a pack, I am left with one sweet. If I keep 5 in a pack, I am left with none. What is the minimum number of sweets I have to pack and distribute?
Correct
Clearly, the required number would be such that it leaves a remainder of 1 when divided by 2, 3 or 4 and no remainder when divided by 5. Such a number is 25.
Incorrect
Clearly, the required number would be such that it leaves a remainder of 1 when divided by 2, 3 or 4 and no remainder when divided by 5. Such a number is 25.
-
Question 51 of 77
51. Question
1 pointsIf a clock takes seven seconds to strike seven, how long will it take to strike ten?
Correct
Clearly seven strike of clock have 6 intervals while 10 strike have 9 intervals.
 Required Time =
Required Time = 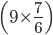 Seconds =
Seconds =  Seconds.Incorrect
Seconds.Incorrect
Clearly seven strike of clock have 6 intervals while 10 strike have 9 intervals.
 Required Time =
Required Time = 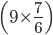 Seconds =
Seconds =  Seconds.
Seconds. -
Question 52 of 77
52. Question
1 pointsIn a group of cows and hens, the number of legs are 14 more than twice the number of heads. The number of cows is
Correct
Let the number of cows be x and the number of hens be y.
Then, 4x + 2y = 2 (x + y) + 14
 4x + 2y = 2x + 2y + 14
4x + 2y = 2x + 2y + 14  2x = 14
2x = 14  x = 7Incorrect
x = 7Incorrect
Let the number of cows be x and the number of hens be y.
Then, 4x + 2y = 2 (x + y) + 14
 4x + 2y = 2x + 2y + 14
4x + 2y = 2x + 2y + 14  2x = 14
2x = 14  x = 7
x = 7 -
Question 53 of 77
53. Question
1 pointsA father tells his son, "I was of your present age when you were born". If the father is 36 now, how old was the boy five years back?
Correct
Let the father's age be x and the son's age be y.
Then, x - y = y or x = 2y,
Now, x = 36. So, 2y = 36 or y = 18.
Therefore Son's present age = 18 years.
So, son's age 5 years ago = 13 years.
Incorrect
Let the father's age be x and the son's age be y.
Then, x - y = y or x = 2y,
Now, x = 36. So, 2y = 36 or y = 18.
Therefore Son's present age = 18 years.
So, son's age 5 years ago = 13 years.
-
Question 54 of 77
54. Question
1 pointsA fires 5 shots to B's 3 but A kills only once in 3 shots while B kills once in 2 shots. When B has missed 27 times, A has killed
Correct
Let's the total number of shots be x. Then,
Shorts Fired By A =

Shorts Fired By A =
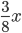
Killing Shorts By A =
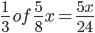
Shorts missed By B =


 or x =
or x = 
Birds Killed by A =
 Incorrect
Incorrect
Let's the total number of shots be x. Then,
Shorts Fired By A =

Shorts Fired By A =
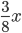
Killing Shorts By A =
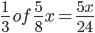
Shorts missed By B =


 or x =
or x = 
Birds Killed by A =

-
Question 55 of 77
55. Question
1 pointsIn a class,
 of the students are girls and rest are boys. If
of the students are girls and rest are boys. If of the girls and
of the girls and of the boys are absent, what part of the total number of students is present?Correct
of the boys are absent, what part of the total number of students is present?Correct
Girls =
 , Boys =
, Boys = 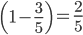
Fraction of student absent =
 =
=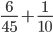 =
=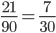
 Fraction of Students Present =
Fraction of Students Present =  =
= 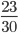 Incorrect
Incorrect
Girls =
 , Boys =
, Boys = 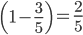
Fraction of student absent =
 =
=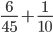 =
=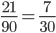
 Fraction of Students Present =
Fraction of Students Present =  =
= 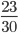
-
Question 56 of 77
56. Question
1 pointsIn a family, a couple has a son and a daughter. The age of the father is three times that of his daughter and the age of the son is half of that of his mother. The wife is 9 years younger to her husband and the brother is seven years older than his sister. What is the age of the mother?
Correct
Let the daughter's age be x years.
Then, father's age = (3x) years.
Mother's age = (3x - 9) years; Son's age = (x + 7) years.
So, x + 7 =

 2x + 14 = 3x - 9
2x + 14 = 3x - 9  x = 23
x = 23Therefore Mother's age = (3x - 9) = (69 - 9) years = 60 years.
Incorrect
Let the daughter's age be x years.
Then, father's age = (3x) years.
Mother's age = (3x - 9) years; Son's age = (x + 7) years.
So, x + 7 =

 2x + 14 = 3x - 9
2x + 14 = 3x - 9  x = 23
x = 23Therefore Mother's age = (3x - 9) = (69 - 9) years = 60 years.
-
Question 57 of 77
57. Question
1 pointsIf a 1 mm thick paper is folded so that the area is halved at every fold, then what would be the thickness of the pile after 50 folds ?
Correct
Since the area is halved on folding, so each time the paper is folded in the center that is it's thickness becomes two fold each time. So, we have:
Thickness after 2 folds =
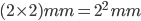
Thickness after 3 folds =
 and so on
and so on The Thickness after 50 folds
The Thickness after 50 folds 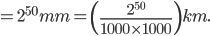
Let's x =
 Then,
Then,
So, log = antilog 9 = 1000000000
Hence, Thickness after 50 folds = x km = 1 billion km.
Incorrect
Since the area is halved on folding, so each time the paper is folded in the center that is it's thickness becomes two fold each time. So, we have:
Thickness after 2 folds =
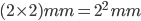
Thickness after 3 folds =
 and so on
and so on The Thickness after 50 folds
The Thickness after 50 folds 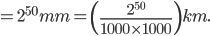
Let's x =
 Then,
Then,
So, log = antilog 9 = 1000000000
Hence, Thickness after 50 folds = x km = 1 billion km.
-
Question 58 of 77
58. Question
1 pointsFirst bunch of bananas has
 again as many bananas as a second bunch. If the second bunch has 3 bananas less than the first bunch, then the number of bananas in the first bunch isCorrect
again as many bananas as a second bunch. If the second bunch has 3 bananas less than the first bunch, then the number of bananas in the first bunch isCorrect
Let's the number of banana in the 2nd bunch be x.
Then, Number of banana in the 1st bunch

So,
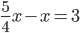
 5x - 4x = 12
5x - 4x = 12 x = 12
x = 12 Number of banana in 1st bunch =
Number of banana in 1st bunch = Incorrect
Incorrect
Let's the number of banana in the 2nd bunch be x.
Then, Number of banana in the 1st bunch

So,
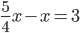
 5x - 4x = 12
5x - 4x = 12 x = 12
x = 12 Number of banana in 1st bunch =
Number of banana in 1st bunch =
-
Question 59 of 77
59. Question
1 pointsMr. X, a mathematician, defines a number as 'connected with 6 if it is divisible by 6 or if the sum of its digits is 6, or if 6 is one of the digits of the number. Other numbers are all 'not connected with 6'. As per this definition, the number of integers from 1 to 60 (both inclusive) which are not connected with 6 is
Correct
Numbers from 1 to 60, which are divisible by 6 are : 6,12,18, 24, 30, 36,42, 48, 54, 60.
There are 10 such numbers.
Numbers from 1 to 60, the sum of whose digits is 6 are : 6, 15, 24, 33, 42, 51, 60.
There are 7 such numbers of which 4 are common to the above ones. So, there are 3such uncommon numbers.
Numbers from 1 to 60, which have 6 as one of the digits are 6, 16, 26, 36, 46, 56, 60.
Clearly, there are 4 such uncommon numbers.
So, numbers 'not connected with 6' = 60 - (10 + 3 + 4) = 43
Incorrect
Numbers from 1 to 60, which are divisible by 6 are : 6,12,18, 24, 30, 36,42, 48, 54, 60.
There are 10 such numbers.
Numbers from 1 to 60, the sum of whose digits is 6 are : 6, 15, 24, 33, 42, 51, 60.
There are 7 such numbers of which 4 are common to the above ones. So, there are 3such uncommon numbers.
Numbers from 1 to 60, which have 6 as one of the digits are 6, 16, 26, 36, 46, 56, 60.
Clearly, there are 4 such uncommon numbers.
So, numbers 'not connected with 6' = 60 - (10 + 3 + 4) = 43
-
Question 60 of 77
60. Question
1 pointsFind the number which when added to itself 13 times, gives 112.
Correct
Let the number be x. Then, x + 13x = 112
 14x = 112
14x = 112  x = 8Incorrect
x = 8Incorrect
Let the number be x. Then, x + 13x = 112
 14x = 112
14x = 112  x = 8
x = 8 -
Question 61 of 77
61. Question
1 pointsAruna cut a cake into two halves and cuts one half into smaller pieces of equal size. Each of the small pieces is twenty grams in weight. If she has seven pieces of the cake in all with her, how heavy was the original cake?
Correct
The seven pieces consist of 6 smaller equal pieces and one half cake piece.
Weight of each small piece = 20 g.
So, total weight of the cake = [2
 (20
(20  6)]g= 240 g.Incorrect
6)]g= 240 g.Incorrect
The seven pieces consist of 6 smaller equal pieces and one half cake piece.
Weight of each small piece = 20 g.
So, total weight of the cake = [2
 (20
(20  6)]g= 240 g.
6)]g= 240 g. -
Question 62 of 77
62. Question
1 pointsA total of 324 coins of 20 paise and 25 paise make a sum of Rs. 71. The number of 25-paise coins is
Correct
Let the number of 20-paise coins be x. Then, number of 25-paise coins = (324 - x).
Therefore 0.20 x x + 0.25 (324 - x) = 71
 20x + 25 (324 - x) = 7100
20x + 25 (324 - x) = 7100 5x= 1000
5x= 1000  x = 200.
x = 200. Hence, number of 25-paise coins = (324 - x) - 124.
Incorrect
Let the number of 20-paise coins be x. Then, number of 25-paise coins = (324 - x).
Therefore 0.20 x x + 0.25 (324 - x) = 71
 20x + 25 (324 - x) = 7100
20x + 25 (324 - x) = 7100 5x= 1000
5x= 1000  x = 200.
x = 200. Hence, number of 25-paise coins = (324 - x) - 124.
-
Question 63 of 77
63. Question
1 pointsA player holds 13 cards of four suits, of which seven are black and six are red. There are twice as many diamonds as spades and twice as many hearts as diamonds. How many clubs does he hold?
Correct
Clearly, the black cards are either clubs or spades while the red cards are either diamonds or hearts.
Let the number of spades be x. Then, number of clubs = (7 - x).
Number of diamonds = 2 x number of spades = 2x;
Number of hearts = 2 x number of diamonds = 4x.
Total number of cards = x + 2x + 4x + 7 - x = 6x + 7.
Therefore 6x + 7 = 13
 6x = 6
6x = 6  x - 1
x - 1Hence, number of clubs = (7 - x) = 6.
Incorrect
Clearly, the black cards are either clubs or spades while the red cards are either diamonds or hearts.
Let the number of spades be x. Then, number of clubs = (7 - x).
Number of diamonds = 2 x number of spades = 2x;
Number of hearts = 2 x number of diamonds = 4x.
Total number of cards = x + 2x + 4x + 7 - x = 6x + 7.
Therefore 6x + 7 = 13
 6x = 6
6x = 6  x - 1
x - 1Hence, number of clubs = (7 - x) = 6.
-
Question 64 of 77
64. Question
1 pointsThe taxi charges in a city comprise of a fixed charge, together with the charge of the distance covered. For a journey of 16 km, the charges paid are Rs. 156 and for a journey of 24 km, the charges paid are Rs. 204. What will a person have to pay for travelling a distance of 30 km?
Correct
Let the fixed charge be Rs. x and variable charge be Rs.y per km. Then,
x + 16y = 156 ...(i) and
x + 24y = 204 ...(ii)
Solving (i) and (ii), we get: x = 60, y = 6.
Therefore Cost of travelling 30 km = 60 + 30 y = Rs. (60 + 30
 6) = Rs. 240.Incorrect
6) = Rs. 240.Incorrect
Let the fixed charge be Rs. x and variable charge be Rs.y per km. Then,
x + 16y = 156 ...(i) and
x + 24y = 204 ...(ii)
Solving (i) and (ii), we get: x = 60, y = 6.
Therefore Cost of travelling 30 km = 60 + 30 y = Rs. (60 + 30
 6) = Rs. 240.
6) = Rs. 240. -
Question 65 of 77
65. Question
1 pointsIf every 2 out of 3 ready made shirts need alterations in the sleeves, and every 4 out of 5 need it in the body, how many alterations will be required for 60 shirts?
Correct
Number of Alterations required in 1 Shirt

 Number of Alterations required in 50 shirts
Number of Alterations required in 50 shirts 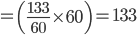 Incorrect
Incorrect
Number of Alterations required in 1 Shirt

 Number of Alterations required in 50 shirts
Number of Alterations required in 50 shirts 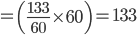
-
Question 66 of 77
66. Question
1 pointsAt the end of a business conference the ten people present all shake hands with each other once. How many handshakes will there be altogether?
Correct
Clearly, total number of handshakes = (9+ 8 + 7 + 6 + 5 + 4 + 3 + 2+1) = 45.
Incorrect
Clearly, total number of handshakes = (9+ 8 + 7 + 6 + 5 + 4 + 3 + 2+1) = 45.
-
Question 67 of 77
67. Question
1 pointsAfter distributing the sweets equally among 25 children, 8 sweets remain. Had the number of children been 28, 22 sweets would have been left after equal distribution. What was the total number of sweets?
Correct
Let the total number of sweets be (25x + 8).
Then, (25x + 8) - 22 is divisible by 28
 (25x - 14) is divisible by 28
(25x - 14) is divisible by 28  28x - (3x + 14) is divisible by 28
28x - (3x + 14) is divisible by 28 (3x + 14) is divisible by 28
(3x + 14) is divisible by 28  x = 14.
x = 14. Total number of sweets = (25
Total number of sweets = (25  14 + 8) = 358.Incorrect
14 + 8) = 358.Incorrect
Let the total number of sweets be (25x + 8).
Then, (25x + 8) - 22 is divisible by 28
 (25x - 14) is divisible by 28
(25x - 14) is divisible by 28  28x - (3x + 14) is divisible by 28
28x - (3x + 14) is divisible by 28 (3x + 14) is divisible by 28
(3x + 14) is divisible by 28  x = 14.
x = 14. Total number of sweets = (25
Total number of sweets = (25  14 + 8) = 358.
14 + 8) = 358. -
Question 68 of 77
68. Question
1 pointsA group of 1200 persons consisting of captains and soldiers is travelling in a train. For every 15 soldiers there is one captain. The number of captains in the group is
Correct
Clearly, out of every 16 persons, there is one captain. So, number of captains
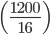 = 75.Incorrect
= 75.Incorrect
Clearly, out of every 16 persons, there is one captain. So, number of captains
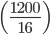 = 75.
= 75. -
Question 69 of 77
69. Question
1 pointsIn a caravan, in addition to 50 hens, there are 45 goats and 8 camels with some keepers. If the total number of feet be 224 more than the number of heads in the caravan, the number of keepers is
Correct
Let number of keepers be x. Then,
Total number of feet = 2 x 50 + 4 x 45 + 4 x 8 + 2x = 2x + 312.
Total number of heads = 50 + 45 + 8 + x= 103 + x.
Therefore (2x + 312) = (103 + x) + 224 or x = 15.
Incorrect
Let number of keepers be x. Then,
Total number of feet = 2 x 50 + 4 x 45 + 4 x 8 + 2x = 2x + 312.
Total number of heads = 50 + 45 + 8 + x= 103 + x.
Therefore (2x + 312) = (103 + x) + 224 or x = 15.
-
Question 70 of 77
70. Question
1 pointsA monkey climbs 30 feet at the beginning of each hour and rests for a while when he slips back 20 feet before he again starts climbing in the beginning of the next hour. If he begins his ascent at 8.00 a.m., at what time will he first touch a flag at 120 feet from the ground?
Correct
Net ascent of the monkey in 1 hour = (30 - 20) feet = 10 feet.
So, the monkey ascends 90 feet in 9 hours i.e. till 5 p.m.
Clearly, in the next 1 hour i.e. till 6 p.m. the monkey ascends remaining 30 feet to touch the flag.
Incorrect
Net ascent of the monkey in 1 hour = (30 - 20) feet = 10 feet.
So, the monkey ascends 90 feet in 9 hours i.e. till 5 p.m.
Clearly, in the next 1 hour i.e. till 6 p.m. the monkey ascends remaining 30 feet to touch the flag.
-
Question 71 of 77
71. Question
1 pointsA number consists of two digits whose sum is 11. If 27 is added to the number, then the digits change their places. What is the number?
Correct
Let the ten's digit be x. Then, unit's digit = (11 - x).
So, number = 10x + (11 - x) = 9x + 11.
Therefore (9x + 11) + 27 = 10 (11 - x) + x
 9x + 38 = 110 - 9x
9x + 38 = 110 - 9x  18x = 72
18x = 72  x = 4.
x = 4.Thus, ten's digit = 4 and unit's digit = 7.
Hence, required number = 47.
Incorrect
Let the ten's digit be x. Then, unit's digit = (11 - x).
So, number = 10x + (11 - x) = 9x + 11.
Therefore (9x + 11) + 27 = 10 (11 - x) + x
 9x + 38 = 110 - 9x
9x + 38 = 110 - 9x  18x = 72
18x = 72  x = 4.
x = 4.Thus, ten's digit = 4 and unit's digit = 7.
Hence, required number = 47.
-
Question 72 of 77
72. Question
1 pointsAn enterprising businessman earns an income of Re. 1 on the first day of his business. On every subsequent day, he earns an income which is just double of that made on the previous day. One the 10th day of business, his income is
Correct
Income on the first day = Re. 1.
Income on the 2nd day = Rs. (1
 2) = Rs. 21.
2) = Rs. 21.Income on the 3rd day = Rs. (21
 2) = Rs. 22 and so on. Thus, Income on the rath day = Rs. 2n-1.
2) = Rs. 22 and so on. Thus, Income on the rath day = Rs. 2n-1.Therefore Income on the 10th day = Rs. 29.
Incorrect
Income on the first day = Re. 1.
Income on the 2nd day = Rs. (1
 2) = Rs. 21.
2) = Rs. 21.Income on the 3rd day = Rs. (21
 2) = Rs. 22 and so on. Thus, Income on the rath day = Rs. 2n-1.
2) = Rs. 22 and so on. Thus, Income on the rath day = Rs. 2n-1.Therefore Income on the 10th day = Rs. 29.
-
Question 73 of 77
73. Question
1 pointsNitin's age was equal to square of some number last year and the following year it would be cube of a number. If again Nitin's age has to be equal to the cube of some number, then for how long he will have to wait?
Correct
Clearly, we have to first find two numbers whose difference is 2 and of which the smaller one is a perfect square and the bigger one a perfect cube.
Such numbers are 25 and 27.
Thus, Nitin is now 26 years old. Since the next perfect cube after 27 is 64,
so required time period = (64 - 26) years = 38 years.
Incorrect
Clearly, we have to first find two numbers whose difference is 2 and of which the smaller one is a perfect square and the bigger one a perfect cube.
Such numbers are 25 and 27.
Thus, Nitin is now 26 years old. Since the next perfect cube after 27 is 64,
so required time period = (64 - 26) years = 38 years.
-
Question 74 of 77
74. Question
1 pointsOn Children's Day, sweets were to be equally distributed among 175 children in a school. Actually on the Children's Day, 35 children were absent and therefore each child got 4 sweets extra. Total how many sweets were available for distribution?
Correct
Let's the total number of sweets be x
Then,
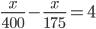
 5x - 4x
5x - 4x  700
700 x = 2800Incorrect
x = 2800Incorrect
Let's the total number of sweets be x
Then,
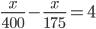
 5x - 4x
5x - 4x  700
700 x = 2800
x = 2800 -
Question 75 of 77
75. Question
1 pointsBetween two book-ends in your study are displayed your five favorite puzzle books. If you decide to arrange the five books in every possible combination and moved just one book every minute, how long would it take you?
Correct
Clearly, number of ways of arranging 5 books = 5 ! = 5 x 4 x 3 x 2 x 1 = 120.
So, total time taken = 120 minutes = 2 hours.
Incorrect
Clearly, number of ways of arranging 5 books = 5 ! = 5 x 4 x 3 x 2 x 1 = 120.
So, total time taken = 120 minutes = 2 hours.
-
Question 76 of 77
76. Question
1 pointsA placed three sheets with two carbons to get two extra copies of the original. Then he decided to get more carbon copies and folded the paper in such a way that the upper half of the sheets were on top of the lower half. Then he typed. How many carbon copies did he get?
Correct
Since the number of carbons is 2, only two copies can be obtained.
Incorrect
Since the number of carbons is 2, only two copies can be obtained.
-
Question 77 of 77
77. Question
1 pointsA printer numbers the pages of a book starting with 1 and uses 3189 digits in all. How many pages does the book have?
Correct
No. of digits in 1-digit page nos. = 1
 9 = 9.
9 = 9.No. of digits in 2-digit page nos. = 2
 90 = 180.
90 = 180.No. of digits in 3-digit page nos. = 3
 900 = 2700.
900 = 2700.No. of digits in 4-digit page nos. = 3189 - (9 + 180 + 2700) = 3189 - 2889 = 300.
 No. of pages with 4-digit page nos. =
No. of pages with 4-digit page nos. =  75.
75.Hence, total number of pages = (999 + 75) = 1074.
Incorrect
No. of digits in 1-digit page nos. = 1
 9 = 9.
9 = 9.No. of digits in 2-digit page nos. = 2
 90 = 180.
90 = 180.No. of digits in 3-digit page nos. = 3
 900 = 2700.
900 = 2700.No. of digits in 4-digit page nos. = 3189 - (9 + 180 + 2700) = 3189 - 2889 = 300.
 No. of pages with 4-digit page nos. =
No. of pages with 4-digit page nos. =  75.
75.Hence, total number of pages = (999 + 75) = 1074.




hye nice question